双曲度大尺寸机身蒙皮零件拉伸成形工艺研究

双曲度大尺寸机身蒙皮零件拉伸成形工艺研究

徐颖 吴楠

航空工业西安飞机工业（集团）有限责任公司飞，陕西 西安 710089

摘要：金属板材成形回弹现象是影响蒙皮零件成形精度的重要因素之一，对回弹变形提前预测能有效控制回弹缺陷的产生。近年来随着计算机仿真模拟应用的发展，在拉伸成形零件的成形回弹预测中，回弹数值模拟技术的运用成为一种重要且有效的分析手段。

关键词：拉伸；回弹；模拟

1 引言

飞机外表面蒙皮外形多为单向双曲度型面，通常采用拉伸成形。但某大尺寸飞机的机身蒙皮，由于机身后部急剧拉高、机身底部与起落架舱交汇、顶部与机翼交汇等原因，造成部分蒙皮曲度变化较复杂，外形存在异向双曲情况，即纵向曲度与横向曲度相反。此类曲度方向相异的蒙皮在采用拉伸成形的工艺方法进行加工时，需对成形工装的外形、成形过程中回弹等方面进行工艺分析^[2]。

2 正文

本文选用大尺寸飞机机身下部一块异向双曲蒙皮作为典型试验案例，此类蒙皮零件生产中采用：拉伸—包覆—拉伸的成形方式。蒙皮成形工装采用铝合金铸造基体，型面选取可加工塑料涂敷后用数控设备加工到最终控制尺寸。一般的同向双曲蒙皮采用型面为凸面的工装拉伸成形，通过对异向双曲蒙皮进行变形模拟受力分析，此类零件采用凹模拉形时，从等效应力分布云图上看，在零件范围内的应力布较均匀，回弹量较小，更有利于获取合格零件。为达到的良好成形效果，异向双曲蒙皮工装结构外形，采用视觉显示为凹模的工装型面。

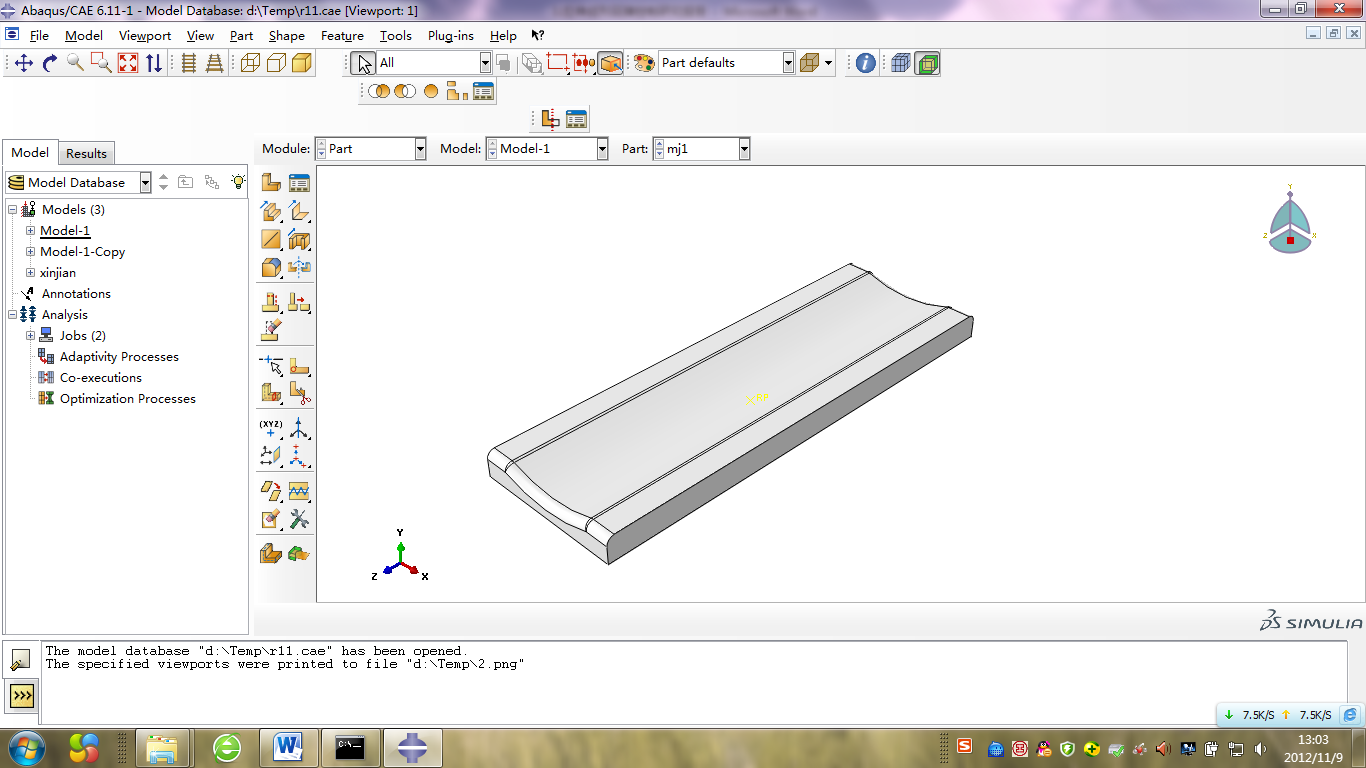
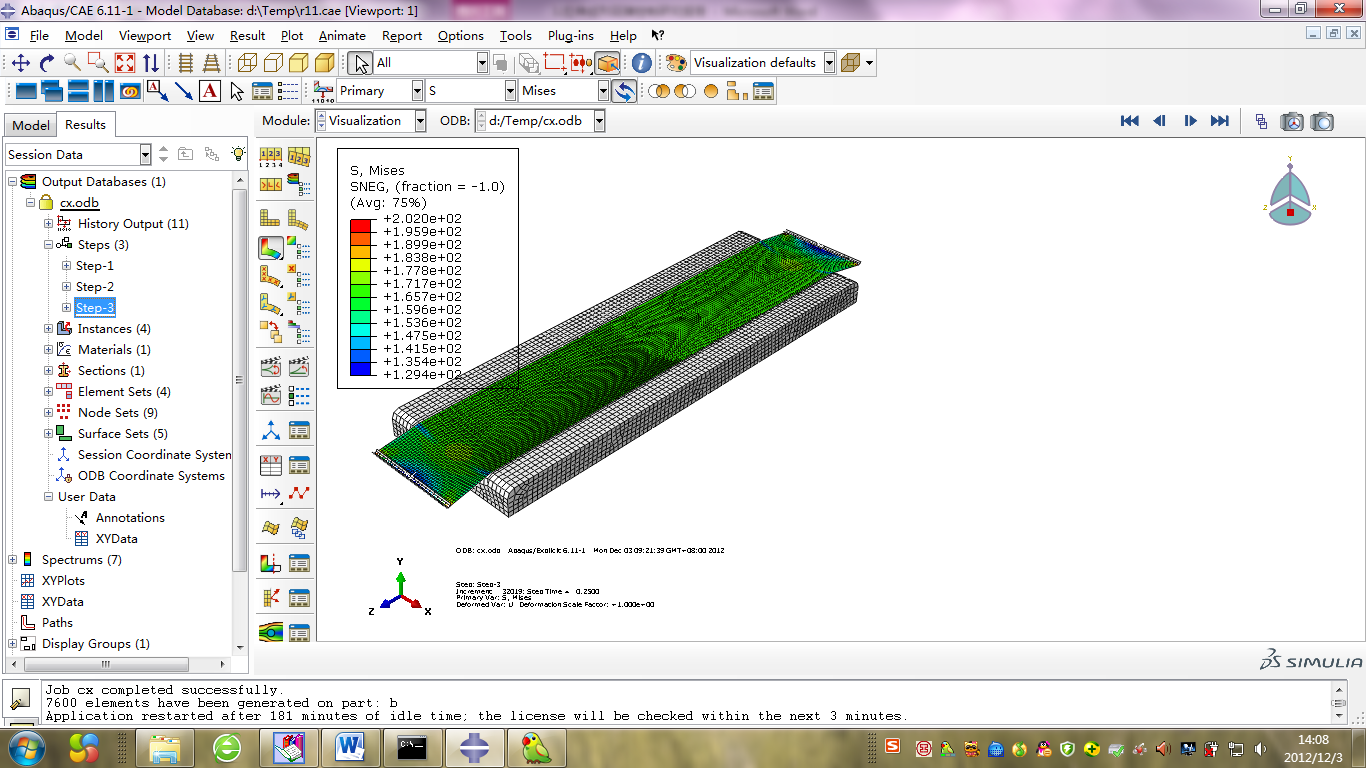
图1 凹模工装 图2 等效应力分布云图

传统回弹的模拟有两种基本方法，无模法和有模法。无模法理论认为零件回弹主要属于弹性问题,可以通过将等效节点力反向加载计算出回弹的最终结果。该方法采用全量法有限元理论进行求解。采用有模法进行仿真时,为了精确模拟零件的非线性卸载过程,必须基于增量型有限元理论采用逐步迭代求解,由于涉及细微增量步和接触摩擦非线性迭代过程,导致计算效率非常低下。许多计算表明,这两种方法用来分析回弹问题得到的计算结果几乎是完全一样的。

此蒙皮零件的成形过程为弹塑性变形，受材料回弹影响，零件最终成形后型面实际外形与工装型面存在一定差异。在工艺参数及模具型面确定的情况下，利用分析较准确且较快捷的无模方法，选择一个横向截面考察其回弹量，其中截面为板料的纵向中心位置，如图3所示，可以准确获取各个节点的回弹量，如图4所示。

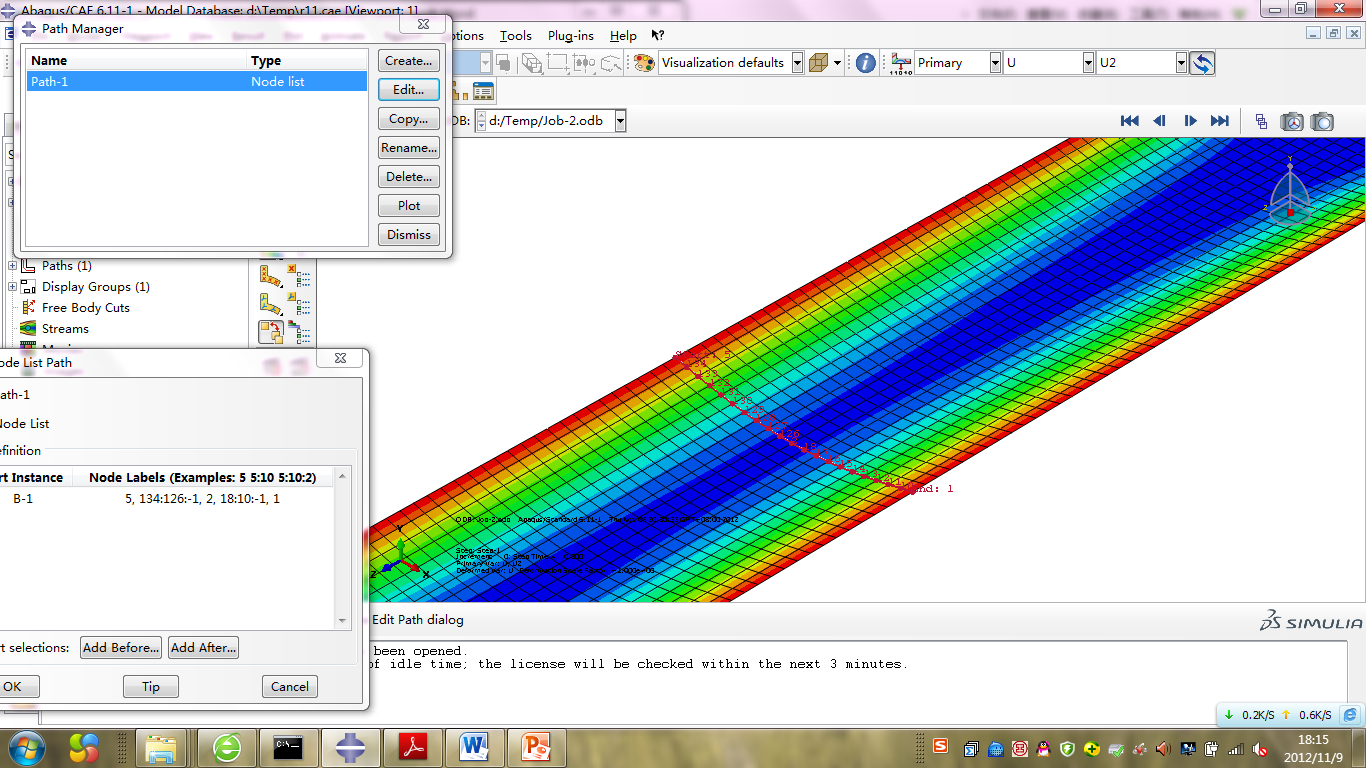
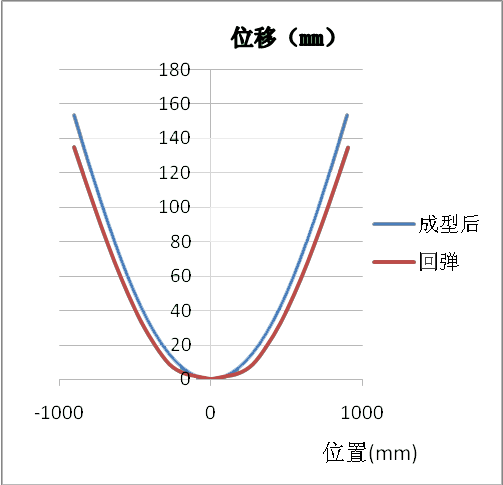
图3横向截面路径 图4截面回弹前后对比u2的值

将毛料卸载前后的位移作为回弹的优化目标，根据回弹计算结果对拉伸工艺参数进行优化，优化算法采用遗传算法，优化模型如下：

目标函数：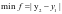

其中y1为设计变量对应的一组回弹量, y2为符合工艺要求的回弹量。

设计变量:单边预拉型长度t1、包覆模具上升位移t2、补拉长度：t3

约束条件:贴膜间隙≤0.5mm

取值范围：100mm≤t1≤150mm, 180mm≤t2≤200mm,40mm≤t3≤80mm

实验最终得到最优工艺参数为单边预拉长度为180mm,模具上升180mm,单边补拉长度为80mm，最大的回弹值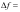 0.43mm。

3 结束语

通过理论分析、数值模拟及工艺试验相结合的方法，合理选择模具结构及拉伸成形工艺参数，能够满足此类蒙皮零件的成形需求，达到设计外形精度，确保了异向双曲大尺寸机身蒙皮的产品质量。

参考文献

1 张克慧主编《塑性材料学》西北工业大学出版社，2008.

2 陈忠阳《飞机金属材料标准与试验方法》机械工业出版社，2009.