中国航发湖南动力机械研究所,湖南 株洲 412002
摘 要:本文对发动机中的关键件涡轮盘的主要失效模式和设计需要考虑的强度问题进行了总结,对某粉末冶金燃气涡轮盘进行了强度分析,并对该涡轮盘进行了强度评估和寿命分析,为该涡轴发动机燃气涡轮盘结构强度设计提供参考.
关键词:涡轴发动机 燃气涡轮盘 强度分析
Mechanical design of Turbine shaft engine turbine disk
Wang Jianfang Zhangyong
(AECC HUNAN Aviation Powerplant Research Institute, Zhuzhou ,China 412002)
Abstract:A procedure of main disabled mode and intensity issue for turbine disk was summarized. The strength of a powder metallurgy gas turbine disk was analyzed and the life of the disk was analyzed. The reference of the structure strength design of gas turbine disk was provided.
Key words:turbine shaft engine;gas turbine disk; mechanical design.
燃气涡轮盘作为航空发动机中的一个关键零件,其承受较高的工作温度和转速,在很多的航空发动机中,涡轮盘的寿命一直是发动机关键件中寿命最短的,其寿命直接决定了发动机的寿命。现代发动机随着性能指标的不断提高,轮盘的工作环境越来越恶劣,为了满足使用要求,粉末冶金材料开始大量应用于燃气涡轮盘上
某涡轴发动机在国内首次采用粉末冶金作为燃气涡轮盘材料,由于制造工艺的局限性,粉末冶金盘不可避免存在一定尺寸的夹杂缺陷,通过对该燃气涡轮盘所用粉末冶金材料开展了夹杂及其位置对粉末冶金材料低周疲劳寿命影响的研究,试验表明,表面夹杂比内部夹杂对寿命影响更大。为了解决此问题,通过大量材料试验得到粉末冶金材料可靠度为99.87%的材料低循环疲劳寿命方程,设计中采用此方程以考虑夹杂等缺陷的影响。
涡轮盘主要的破坏形式有:
涡轮盘榫槽处出现裂纹和断裂,见图1;
轮心出现裂纹;
轮盘偏心孔处出现裂纹;
轮盘子午截面破裂;
蠕变损伤,导致轮盘破裂。
以上几种为涡轮盘常见的几种破坏形式,为了防止轮盘出现破坏,提高设计安全裕度,在设计阶段必须对涡轮盘各种可能的破坏形式进行详细的强度设计分析,从而保证涡轮盘的强度。

榫槽底部断裂

图1 某燃气涡轮盘断裂示意图
根据涡轮盘的可能破坏形式,涡轮盘强度设计需要考虑的主要内容有:
1)涡轮盘榫槽的静强度设计;
2)涡轮盘盘体静强度设计;
3)涡轮盘盘体持久静强度设计;
4)涡轮盘榫槽低循环和持久寿命设计;
5)涡轮盘盘体低循环和持久寿命设计;
6)涡轮盘破裂转速。
根据该燃气涡轮盘的装配关系,应力分析需考虑的载荷有:
1)各状态转速;
2)各状态温度;
3)叶片离心力;
4)中心拉杆拉力。
榫槽主要考核榫齿图2的D-D截面的拉伸应力、榫齿面挤压应力和榫齿根部的剪切应力、弯曲应力的等效应力。其常规计算的主要公式为:
拉伸应力计算公式:
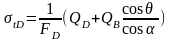 ............(1)
............(1)
式中:
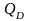 —轮盘凸缘D-D截面以上部分的离心力;
—轮盘凸缘D-D截面以上部分的离心力;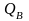 —整个叶片的离心力;
—整个叶片的离心力;
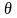 —齿面承力面法线与榫槽对称中心线的夹角;
—齿面承力面法线与榫槽对称中心线的夹角;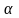 —齿面承力面法线与榫头对称中心线的夹角;
—齿面承力面法线与榫头对称中心线的夹角; —D-D截面的面积。
—D-D截面的面积。
剪切应力和弯曲应力计算公式: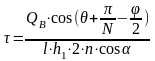 ............(2)
............(2)
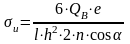 ............(3)
............(3)
式中:
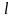 —榫齿轴向长度;
—榫齿轴向长度;
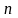 —榫齿对数目;
—榫齿对数目;
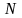 —轮盘凸缘个数;
—轮盘凸缘个数;
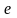 —榫齿接触面法向力的力臂。
—榫齿接触面法向力的力臂。
等效应力计算公式:
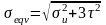 ................(4)
................(4)
挤压应力计算公式:
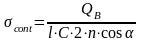 ............(5)
............(5)
式中:C—榫齿接触面宽度。
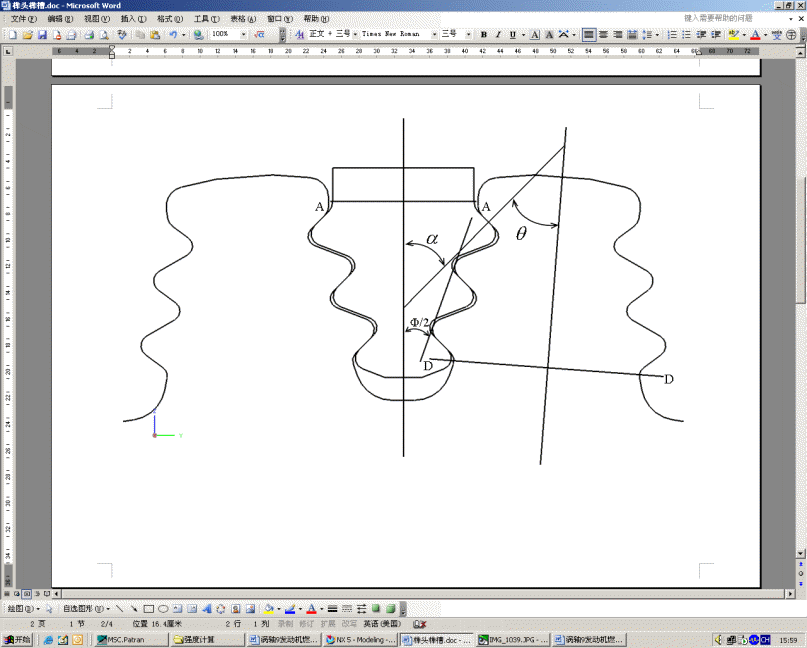
图2 榫槽结构示意图
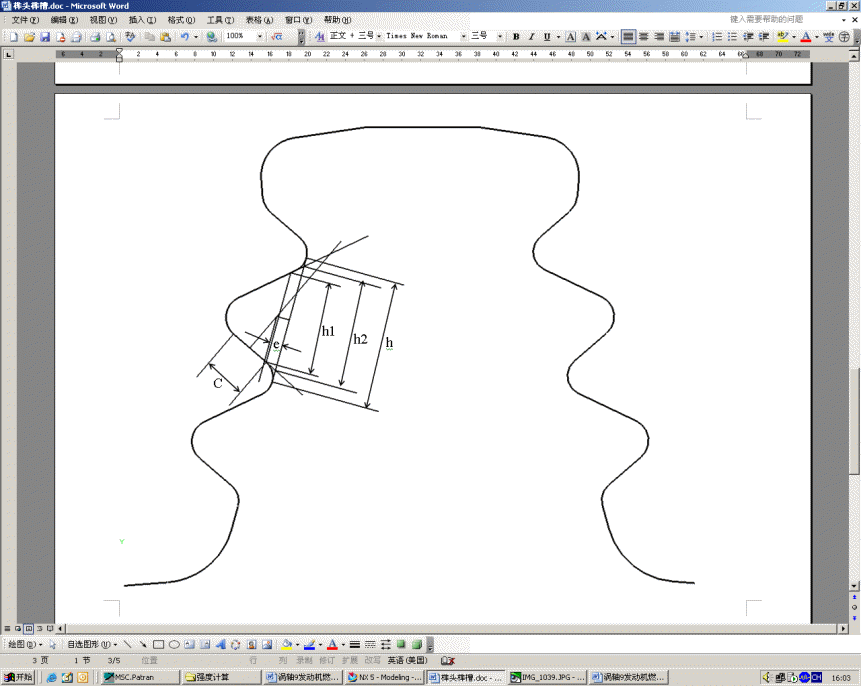
图3 轮盘凸缘结构示意图
目前榫齿的强度校核都是基于常规计算得到的应力,故本文的榫齿应力分析同样基于常规分析方法。通过计算涡轮盘榫槽拉伸应力
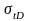 =407.9MPa,剪切应力
=407.9MPa,剪切应力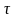 =235.9MPa,弯曲应力
=235.9MPa,弯曲应力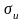 =114.5MPa,等效应力
=114.5MPa,等效应力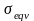 =424.3MPa,挤压应力
=424.3MPa,挤压应力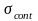 =597.2MPa。
=597.2MPa。
采用MSC.Patran对该燃气涡轮盘进行有限元前后处理,采用MSC.Nastran进行线弹性有限元分析。轮盘载荷和结构具有循环对称性,共有43个榫槽,本文取包含一个完整榫槽在内的1/43循环对称段作为计算模型,采用二十节点六面体单元进行网格划分。约束和载荷施加如下:
1)约束图4所示A处的轴向位移和一个节点的周向位移;
2)叶片离心力转换成面力施加在轮盘榫齿接触面上;
3)中心拉杆轴向力以面力形式施加在图4的B处;
4)温度载荷以节点温度形式施加在模型上。
在起飞状态下的当量应力分布见图6,其最大当量应力位于轮心。


B
A
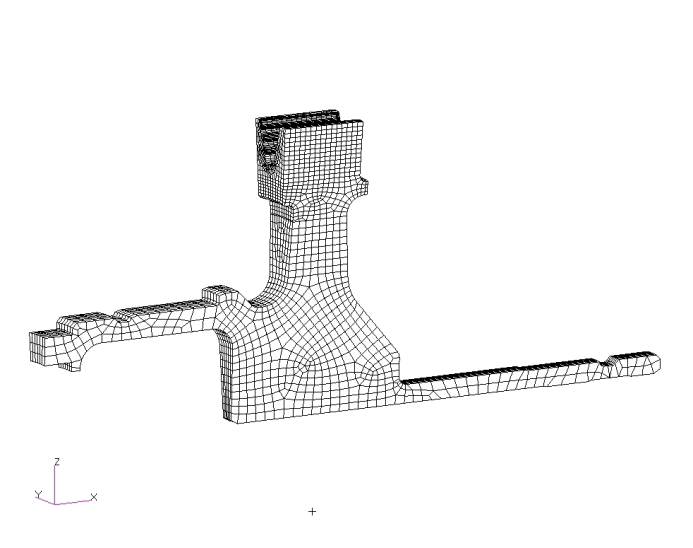
图4 燃气涡轮盘有限元网格
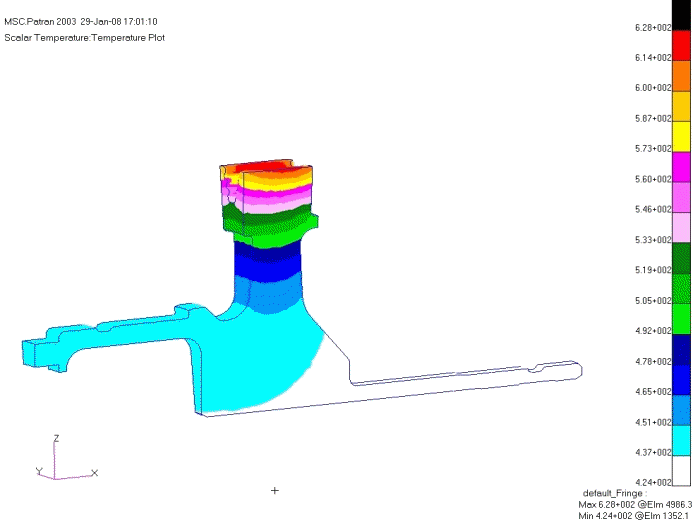
图5 燃气涡轮盘温度场(单位:℃)

图6 燃气涡轮盘当量应力(单位:MPa)
对涡轮盘进行静强度校核,校核结果见表5。
表1 涡轮盘强度校核
| 应力类型 | 应力标准 | 安全系数 |
| 最大离心径向应力 | 0.75 | 1.15 |
| 最大离心径向应力 | 0.6 | 1.18 |
| 平均周向应力 | 0.75 | 1.29 |
| 平均周向应力 | 0.6 | 1.35 |
| 内径处周向应力 | 0.95 | 1.02 |
| 辐板处周向应力 | 0.85 | 1.34 |
| 榫齿颈部拉伸应力 | 0.4 | 1.02 |
持久强度储备计算公式:
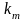 =
=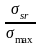 ..................(6)
..................(6)
式中:
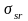 —持久强度,由于工况较多,将其它状态时间折合到起飞状态时间,取起飞状态时间的两倍;
—持久强度,由于工况较多,将其它状态时间折合到起飞状态时间,取起飞状态时间的两倍;
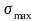 —最大当量应力。
—最大当量应力。
轮心持久强度储备系数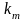 =1.34。
=1.34。
由于榫齿温度较高,取起飞时间的两倍进行持久强度校核发现其储备系数不能满足要求,本文分别将各状态的持久强度储备系数求出,然后求持久静强度局部当量储备值。方法如下:
根据各应力计算了各状态的最小持久静强度局部储备系数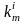 ,
,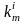 的计算公式如下:
的计算公式如下:
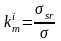 ..................(7)
..................(7)
式中:
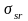 -持久强度;
-持久强度;
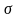 -应力。
-应力。
根据各状态的最小持久静强度局部储备系数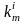 ,可由以下公式[8]求得持久静强度局部当量储备值
,可由以下公式[8]求得持久静强度局部当量储备值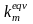 。
。
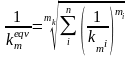 ............(8)
............(8)
式中:
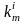 —
— 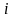 状态下的持久静强度局部储备系数;
状态下的持久静强度局部储备系数;
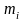 —
— 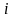 状态的持久强度指数;
状态的持久强度指数;
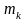 — 换算状态的持久强度指数;
— 换算状态的持久强度指数;
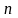 — 轮盘经历的工作状态数目。
— 轮盘经历的工作状态数目。
持久强度指数采用如下方程得到:
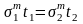 ...................(9)
...................(9)
式中:
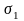 ,
,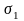 —对应同一温度,时间为
—对应同一温度,时间为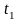 和
和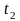 的持久强度;
的持久强度;
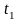 ,
,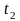 —持久时间。
—持久时间。
通过计算拉伸应力、等效应力和挤压应力持久静强度局部当量值分别为2.61、2.53和1.90。
通过大量的材料试验,得到了可靠度为99.87%的材料低循环疲劳寿命方程,设计中采用此方程以考虑夹杂等缺陷的影响。
表2 FGH95试样夹杂对低循环疲劳寿命影响
| 试样夹杂位置 | 疲劳寿命(次)(538℃,应变幅/平均应变=0.95,最大应变=0.78%) |
| 表面夹杂 | 9263、10512、 17162、11646、16758 |
| 内部夹杂 | 45147、45046、23111、49049、69145 |
采用FGH95低循环应变-寿命曲线对轮心进行寿命预测,FGH95在600℃时对称循环下的应变-寿命曲线(γ=95%,P=99.87%)为 :
t/2 = (f/E)(2Nf)b + f(2Nf)c.....(10)
循环应力-应变曲线为:
t/2 = (/2E) + (/2K)1/n...(11)。
在考虑平均应力的情况下应变-寿命曲线为 :t/2 = ((f-m)/E)(2Nf)b + f(2Nf)c。其中:f=2029MPa,b=-0.096,f=1.67%,c=-0.41,K=1584MPa,n=0.042,m为平均应力。对轮体上应力最大位置(轮心)进行低循环疲劳寿命计算,计算结果见表3。
表3 轮盘低循环疲劳寿命
| 发动机工作循环 | 考虑分散系数之后的寿命 |
| 主循环I | 7630 |
| 主循环II | 11465 |
| 次循环I | >105 |
| 次循环II | >105 |
| 次循环III | >105 |
考虑分散系数之后的燃气涡轮盘轮体寿命为7630次。
采用Miner[2]线性累积损伤理论进行寿命估计。在一定工作时间内的总损伤:
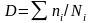 ...................(12)
...................(12)
式中:
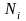 —在某工作循环下的循环数寿命;
—在某工作循环下的循环数寿命;
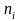 —在一定工作时间内对应寿命
—在一定工作时间内对应寿命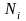 工作循环的工作次数。
工作循环的工作次数。
零件的破坏准则为:
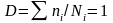 ................(13)
................(13)
用线性累积损伤理论计算涡轮盘轮体的小时数寿命:
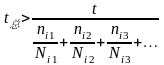 ...........(14)
...........(14)
式中:
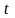 —表示时间;
—表示时间;
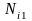 ,
,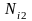 ,
,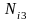 ——对应各工作循环下的循环数寿命;
——对应各工作循环下的循环数寿命;
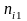 ,
,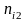 ,
,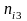 —在
—在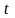 时间内,对应寿命为
时间内,对应寿命为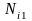 ,
,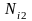 ,
,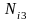 的工作循环工作次数。
的工作循环工作次数。
通过计算得到燃气涡轮盘小时数寿命为4900小时。
在发动机设计规范中对轮盘的破裂转速做了严格要求,涡轮盘的破裂形式分为两种,一种是轮盘子午截面破裂,一种为圆柱截面破裂,采用如下两个公式计算轮盘子午和圆柱截面破裂转速:
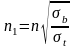 ...................(15)
...................(15)
式中:
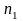 -子午截面破裂转速;
-子午截面破裂转速;
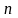 - 设计转速;
- 设计转速;
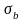 -强度极限;
-强度极限;
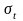 -子午截面平均周向应力。
-子午截面平均周向应力。
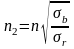 ................(16)
................(16)
式中:
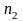 -圆柱截面破裂转速;
-圆柱截面破裂转速;
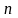 - 设计转速;
- 设计转速;
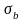 -强度极限;
-强度极限;
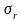 -圆柱截面平均径向应力。
-圆柱截面平均径向应力。
子午截面破裂比=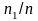 ,圆柱截面破裂比=
,圆柱截面破裂比=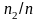 。
。
通过计算得到该涡轮盘子午和圆柱截面破裂比分别为1.47和1.43,满足设计标准要求。
燃气涡轮盘需要考虑的强度试验主要有:低循环疲劳试验和超转破裂试验。
由于试验台无法模拟发动机工作时涡轮盘的真实温度场,故需要进行试验载荷等效,根据试验状态下的温度进行转速转换,使试验效果等同于发动机中规定要求达到的效果。
对于低循环等效主要是根据寿命相等原则进行试验转速转换,转换的方法为:
根据实际情况,选择涡轮盘的一个部位作为低循环疲劳试验的考核部位,主要的部位有轮心、榫槽和偏心孔。发动机上的标准应力循环为:0—最大—0,试验循环为:试验下限转速—试验上限转速—试验下限转速。根据试验器系数1.0确定上限转速。
试验器系数计算公式[4]为:  =
=
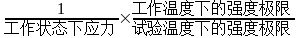
根据试验器系数1.0,求得到上限转速下应力值。根据上限转速应力值,反推工作转速。计算得到的低循环疲劳试验转速为46075r/min。
超转试验主要考核轮盘在超转情况下,轮盘可能发生较大的塑性变形还能否正常可靠工作。破裂试验用于保证轮盘的静强度。基于超转试验的目的,目前有两种等效方法,一是在破裂比相当原则,既在发动机超转试验条件下的子午截面和圆柱截面破裂转速与超转转速之比等于试验条件的子午和圆柱截面破裂转速与试验条件下的等效超转转速之比。即:
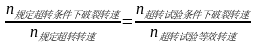 ,
,
二是轮心区域屈服储备系数相当原则。即:
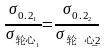
式中:
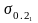 -对应规定超转条件下轮心应力最大处屈服极限;
-对应规定超转条件下轮心应力最大处屈服极限;
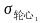 -对应规定超转条件下轮心最大当量应力;
-对应规定超转条件下轮心最大当量应力;
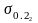 -对应超转试验条件下轮心应力最大处屈服极限;
-对应超转试验条件下轮心应力最大处屈服极限;
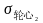 -对应超转试验条件下轮心最大当量应力。
-对应超转试验条件下轮心最大当量应力。
目前超转试验等效主要是基于第一种方法,即破裂比相当原则原则进行等效转速分析。
对于破裂试验转速的等效原则是破裂比相当,即:
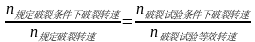
使用以上方法计算得到超转和破裂试验转速分别为53431r/min和56459r/min。
根据以上方法确定的试验等效转速,进行了该粉末冶金涡轮盘超转15%、破裂试验及规定寿命要求的循环疲劳试验,试验后检查表明:涡轮盘没有出现裂纹。该涡轮盘已随发动机完成了首翻期和低循环疲劳试验。试验也表明该发动机涡轮盘具有足够的强度和寿命。
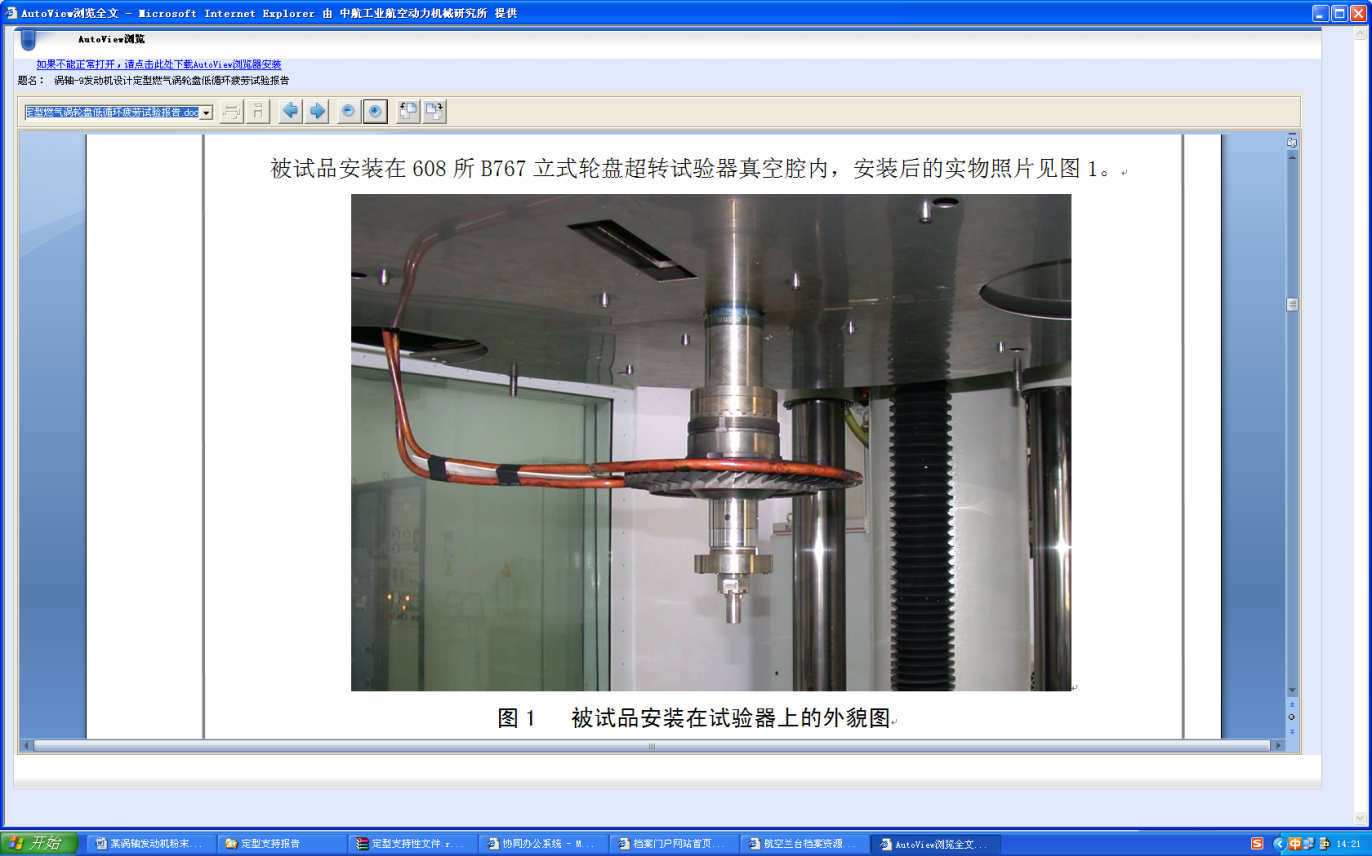
图7 燃气涡轮盘低循环、超转和破裂试验
本文对涡轮盘可能的破坏形式进行了分析,对强度分析需要考虑的内容进行了总结。并对国内首次使用粉末冶金的某燃气涡轮盘强度、寿命设计进行了详细的设计分析,并通过试验得到了验证,目前装该涡轮盘的发动机工作稳定,静强度和寿命均满足设计要求。
[1] 吕文林. 航空发动机强度计算.国防工业出版社, 1988.
[2] 陈传尧. 疲劳与断裂. 华中科技大学出版社. 2002.
作者简介:王建方,男,1980年8月生,高级工程师,主要研究方向:航空发动机结构强度
通信作者:王建方,hnwjf@163.com