电子科技大学成都学院 四川省成都市 610000
摘要:为解决桥面上的拥堵问题,有人提出了在大桥起始端设置停车线并用信号灯控制车辆进入桥面的阻断式限流法。本文对实施阻断式限流法后进行,车辆行驶时间和桥的长度进行分析和求解。
问题一:当大桥开始拥堵时段管理模式后,会造成截断点后续车流速度减慢,经过多长时间后续车流回到稳定车流状态,求解稳定状态的平均车速。这是一个排队论问题,首先需要利用数据求解分布规律,需要用计算机仿真出数据,这里根据题目已知的数据和参考文献,求解出参数的大概范围。利用Matlab仿真出1000次的排队场景,最终求解出来经过了8.3分钟后回到平均车速为23.7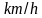 ,
,
问题二:目标求出车辆在限流之前和限流之后的平均车速。本题和第一问类似,相比第一问本题需要求出两次状态的平均车速,在第一问求解时两次状态的平均车速已经求出,只是没有筛选出来,本问题在第一问的基础上建立筛选模型,利用Matlab求解出限流之前平均车速为18.4,限流之后为23.5。
关键词:排队论;泊松分布;计算机模拟
问题重述
问题一:假设有桥面长100米,桥的两端各有1公里的一个总长为2100米的路段。当大桥开始拥堵时段管理模式后,会造成截断点后续车流速度减慢,请问大约经过多长时间后续车流回到稳定车流状态,稳定状态的平均车速是多少?
问题二:假设有桥面长100米,桥的两端各有1公里的一个总长为2100米的路段。当大桥采用拥堵时段管理模式一段时间进入后续车流稳定状态后,请先给出一辆车走完整个路段所使用的时间,然后给出按如上阻断式限流法控制车流的方案,一辆车走完整个路段所使用的时间;
模型的建立与求解
5.1.1、仿真模型的建立
车辆通过桥梁路段的过程, 可以从三个方面来描述:到达时刻、车辆进入桥梁路段的速度、在桥梁上行驶的时长。
通过K-S检验可知,车辆达到时间服从泊松分布,车辆进入桥梁路段的速度服从正态分布,桥梁上行驶速度服从负指数分布。
5.1.2、仿真模型的建立
在此利用极大似然估计来确定泊松分布的参数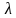 。
。
若总体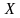 为离散型,其概率分布为
为离散型,其概率分布为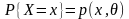 ,
,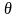 是待估及参数,
是待估及参数,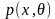 表示估计参数为
表示估计参数为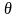 时发生x的概率。当(
时发生x的概率。当(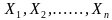 )的一组观测值为(
)的一组观测值为(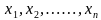 )时,
)时,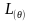 就是样本的似然函数。
就是样本的似然函数。
已知
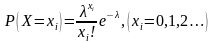
则极大似然函数为
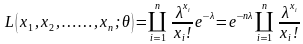
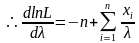
5.1.3、仿真模型的求解
到达时刻服从泊松分布,通过Matlab求解可得到到达时刻的期望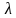 为15.6333,然后利用计算机仿真得到数据如下:
为15.6333,然后利用计算机仿真得到数据如下:
表 1 到达车辆个数
| 到达车辆个数 | 15 | 17 | 16 | 12 | 12 | 17 | 18 | 11 | 8 | 21 |
| 到达时刻 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
桥上的时间服从负指数分布,通过Matlab求解可得到桥上时间的期望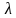 为27.2874,然后利用计算机仿真得到数据如下:
为27.2874,然后利用计算机仿真得到数据如下:
表 2 桥上行驶时间
| 桥上时间 | 21.2 | 15.7 | 7.5 | 40.0 | 15.0 | 6.4 | 24.0 | 8.2 | 19.0 |
| 仿真次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
汽车速度服从正态分布,通过Matlab求可得汽车速度正态分布的期望为15方差为15,然后利用计算机仿真得到数据如下:
表 3 行驶速度
| 速度 | 12.1 | 17.5 | 26.3 | 23.5 | 8.7 | 28.6 | 4.7 | 14.6 | 30.1 |
| 仿真次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
5.2.1、问题一模型的建立
将桥面看作是一段路,然后将在限流管理时能够一次性经过桥面的车辆看作一个整体,所以这个整体从进入桥面到离开桥面所行驶的距离是2倍桥面的距离,假设在桥面行驶的速度为30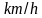 ,这个看作火车的物体最多能由6辆车组成,即截流管理时,每一次绿灯能够放行6辆小汽车,耗时24 s,因此当开启截流管理模式时,平均24秒到达车辆的个数小于6辆时,才可以关闭截流管理模式,通过上一节产生的模拟数据,可以明确的发现,每24s所产生的小汽车的数量是小于6辆的,正好符合本文解决本问题的必要条件。
,这个看作火车的物体最多能由6辆车组成,即截流管理时,每一次绿灯能够放行6辆小汽车,耗时24 s,因此当开启截流管理模式时,平均24秒到达车辆的个数小于6辆时,才可以关闭截流管理模式,通过上一节产生的模拟数据,可以明确的发现,每24s所产生的小汽车的数量是小于6辆的,正好符合本文解决本问题的必要条件。
此题属于车辆到达时间属于泊松分布,有单个服务台,车辆源无限,排队空间有限,排队规则属于等待值,因此本文得出如下平衡方程:
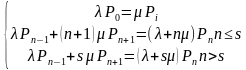
其中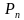 为有
为有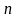 辆小汽车进入桥面的概率;
辆小汽车进入桥面的概率;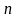 为截流时一次进入桥面的小汽车速量;
为截流时一次进入桥面的小汽车速量;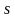 表示在截流状态下一次绿灯最多可以释放的小汽车速量;
表示在截流状态下一次绿灯最多可以释放的小汽车速量;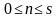 表示系统内有
表示系统内有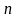 辆小汽车正在桥面上行驶,其余
辆小汽车正在桥面上行驶,其余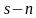 个处于空闲状态,表示没有小汽车在排队。
个处于空闲状态,表示没有小汽车在排队。
利用递推法求解上个式子所示的方程,可得小汽车在截流管理模式下能够进去桥面的概率为:
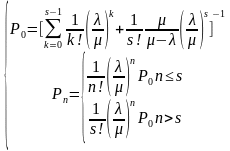
由此可得到截流管理系统的运行指标如下。桥面通过强度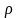 为:
为:
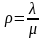
再来车辆必须等待时间:
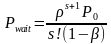
假设此时此刻刚进入桥面车辆编号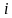 ,缓冲区的车辆的平均速度为
,缓冲区的车辆的平均速度为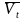 。恢复秩序所需要的时间
。恢复秩序所需要的时间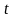 也就是堵车的时间等于每一次完整放行所需要的时间相加。 恢复秩序过后的平均速度
也就是堵车的时间等于每一次完整放行所需要的时间相加。 恢复秩序过后的平均速度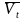 等于还没有上桥的所有车辆的速度相加除以车辆总数。
等于还没有上桥的所有车辆的速度相加除以车辆总数。
因此得到总模型:
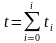
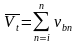
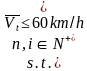
5.2.2、问题一模型的求解与检验
通过Matlab软件进行求解,求得每辆车从一公里行驶开头到桥头的平均车速,再统计单位时间内经过几辆车,就可以求得当时状态下的平均车速。
利用计算机模拟的方法对模型加以检验。通过高速高速公路的历史数据,求得车辆到达时刻符合泊松分布,在统计245辆车的基础上确定了当前时刻的平均车速。最终求解出来经过了8.3分钟后回到平均车速为23.7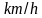
5.2.3、问题二的模型建立
该问题需要求解在进入后续车流稳定状态后需要求的车走完整个路段所使用的时间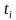 ,则平均时间则为:
,则平均时间则为:
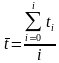
如果在进行截流管理模式下一辆车去要走完整个路段所使用的时间为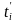 ,则平均时间则为:
,则平均时间则为:
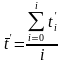
5.2.4、问题二的求解
如果状态已经达到了稳定状态说明当前的平均车速度大于20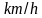 。在初始状态的时候,车辆到达桥头的时候,记录一次前一公里的平均车速,当前平均车速小于20KM/H的时候开启阻断式限流法,通过正态分布仿真可以求得车辆速度的分布列,模拟平均车速度为:
。在初始状态的时候,车辆到达桥头的时候,记录一次前一公里的平均车速,当前平均车速小于20KM/H的时候开启阻断式限流法,通过正态分布仿真可以求得车辆速度的分布列,模拟平均车速度为:
表 4 车辆速度的分布列
| 模拟次数 | 1 | 2 | 3 | 4 | 5 | 998 | 999 | 1000 |
| 稳态时间 | 19.3 | 22.4 | 23.4 | 23.6 | 24.1 | 18.1 | 14.7 | 19.2 |
通过模拟1000次可以发现稳定状态下平均车速大概在18.4左右,经过阻断式限流法控制车流后车速提升为23.5左右。
3