基于模糊综合评价的出租车资源配置模型

基于模糊综合评价的出租车资源配置模型

赵洋 1 陈毅航 2 黄业清 3

1. 华北理工大学 人工智能学院 2. 华北理工大学 理学院 3. 华北理工大学 冀唐学院

摘要：出租车是我国居民日常出行的重要工具之一，“打车难”问题存在已久。本文主要基于模糊综合评价模型、偏大型正态分布隶属函数及多元非线性拟合建立模型并求解出租车资源配置问题。

关键字：模糊综合评价思想；偏大型正态分布隶属函数；非线性规划模型；出租

车资源配置

研究范围的确定

为使研究评价体系具有代表性，我们选取北京、成都、宁波3座不同发展水平的城市。选取里程利用率，车辆满载率∁，万人拥有量作为主要指标。北京生活节奏快，人口密集，交通压力较大，可以代表发展程度较好的一类城市；成都山地较多，地形杂；宁夏为西部城市，相较广大中东部地区经济水平较低，可以代表西部各省市的一般水平。

出租车资源配置评价模型求解

对第一个城市成都，由万人拥有量，里程利用率，车辆满载率，服务率等指标构成权重向量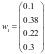 ,评价分 。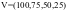

_{同样针对北京和宁夏两个城市各自构成权重向量。得成都、宁夏、北京这3座城市的综合评价矩阵。}

_{综合评价结果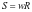}，经计算得3座城市的综合评价结果 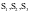分别为：

S₁=,S₂=,

S₃=，由可以得出成都，宁夏，北京三个城市的最终评价分数为：G₁=S₁V₁^T=80.0556，G₃=S₂V₂^T=90.0556，G₃=S₃V₃^T=92.1806。

北京供求匹配程度较小；而成都供求匹配程度较大。

补贴方案吸引力函数

打车软件服务平台推出补贴方案对出租车司机的吸引程度其隶属函数如下所示:

补贴与使用打车软件后增加收益为日常平均工资的约20%左右时可看作吸引力A的中位数。当时，取到，μ_A就是吸引力中位数，可计算出实力因子λ=。

由隶属函数模型可得

式中x代表不同补贴方案的单笔交易补贴金额。

本文找到北京海淀区一天中各个时刻以及经度纬度数据，打车难易程度。

将其进行聚类使相近的点聚集为若干处，以中心点的坐标为某一天的打车难易度。

难易度聚类

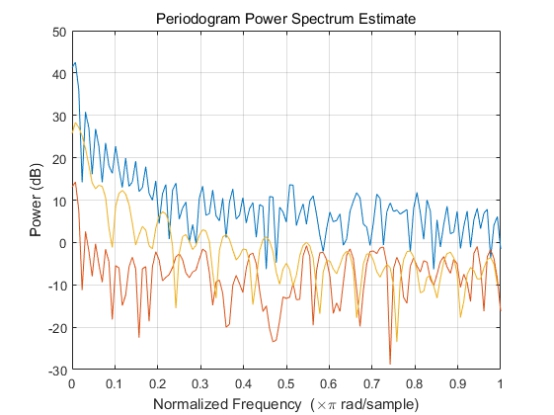
图2-9 补贴方案的周期功率谱密度估计图

由上图可知数据进行补贴方案的周期功率谱密度估计图可得坐标位置与补贴方案的波动有强相关性，打车难易度与补贴方案为不是线性关系。

补贴方案模型的建立

分析补贴方案合理性时应综合考虑公司运行成本，吸引力大小和顾客满意度三方面因素。其中运营成本可由每单补贴 x 反映，补贴方案对司机的吸引力大小用_A 表示。

(3-7)

A,B,C为权重数，取值分别为0.2,0.01,0.45；此外补贴金额x 应满足约束。

为了达到最佳补贴金额，打车软件平台希望出租车吸引力减少得越少越好，即尽量大；另一方面要求顾客满意度更大，即P（x）尽量大。因此公司的最优补贴方案应是使W(x)取最大。

评价补贴方案函数：。

(3-8)

补贴方案模型的求解

利用 matlab遗传算法工具箱对评价补贴方案合理性非线性规划模型进行求解，结果为当每单补贴金额x为8.56时，W(x)有最大值；因为x在约束范围内，所以评判准确，结论合理。

参考文献

[1]费威，马跃，李泊宁，李昆.我国城市出租车资源供求匹配程度研究[D].东北财经大学,2016.

[2]周小梅，田定远．对我国城市出租车行业管制问题的思考---从出租车司机和乘客利益变化角度的分析[J]．价格理论与实践，2011，(8):29-30.

[3]张凤林，王利．我国城市出租汽车行业管理研究[J]．现代城市研究，2012，(10)：99-104．

[4]邵燕斐，王小斌．基于博弈论视角的出租车价格管制困境破解[J]．开发研究，2014，(2)：139-143．

[5]刘鸿江.打车软件对出租车市场的影响研究[J].商业文化, 2014(6).

[6]刘佳倩，朱家明,李之好,李金玲. “互联网 +”时代出租车供需匹配测度及补贴方案效应分析[J].上海工程技术大学,2015(4).

2