义乌工商职业技术学院, 浙江 义乌 322000
摘要:研究灰色理论和统计回归理论在建筑垃圾预测中的应用,分析建筑垃圾产量预测的准确性。根据历史数据分别构建义乌市建筑垃圾的GM(1,l)预测模型和三元线性回归模型,预测未来5年义乌市建筑垃圾“可直接利用量”、“需处理后再利用量”和“总量”。灰色建模前,对原始数据序列进行2阶弱化处理和一次累加生成运算。分析表明:对于少信息的建筑垃圾预测而言,灰色模型预测的精度更高,预测的数据更有参考价值。线性回归分析模型不适合义乌市建筑垃圾预测。灰色预测结果将为义乌市政府对建筑垃圾进行科学管理,垃圾资源化利用提供数据支撑。
关键词:建筑垃圾;灰色;回归;模型;预测
1 前言
义乌市最近几年大规模进行旧城改造、城市有机更新和基础设施建设,产生了大量建筑垃圾,建筑垃圾产量预测成为一个重要的研究方向。但是准确预测建筑垃圾产量存在较大难度,一方面是建筑垃圾历史统计数据较少,另外一方面是建筑垃圾的产量受经济和社会不确定性因素影响较大。目前已有关于建筑垃圾产量预测方法有的模型所需的参数值不容易确定,增加了预测难度,或者方法需要数据量大,数据不易收集,或者预测方法单一,没可比性[1-5]。本文根据灰色理论和统计回归模型分别构建义乌市建筑垃圾的预测模型,预测未来5年义乌市建筑垃圾“可直接利用量”、“需处理后再利用量”和“总量”,对比分析两种模型预测效果,探究预测模型的适用性。
2 义乌市建筑垃圾灰色预测模型构建
2.1 建筑垃圾灰色模型数据处理
设义乌市建筑垃圾总量为Y总、建筑垃圾可直接利用量为Y直、建筑垃圾需处理后再利用量为Y后,义乌市GDP为x1 ,商品房销售面积为x2,建筑施工面积为x3,通过查阅文献和估算等方法获取2008-2017年度义乌市建筑业相关经济数据见表1[6-7]。
表1 2008-2017年度义乌市建筑业相关经济数据
| 年度 | Y总(万吨) | Y直(万吨) | Y后(万吨) | x1 (亿元) | x2 (万m2) | x3 (万m2) |
| 2008 | 80 | 48 | 32 | 493 | 70 | 991 |
| 2009 | 90 | 60 | 30 | 519 | 75 | 1190 |
| 2010 | 91 | 60 | 30 | 614 | 87 | 1199 |
| 2011 | 83 | 50 | 33 | 726 | 72 | 1165 |
| 2012 | 93 | 55 | 38 | 802 | 42 | 1238 |
| 2013 | 236 | 130 | 106 | 882 | 28 | 1430 |
| 2014 | 430 | 251 | 179 | 968 | 55 | 1608 |
| 2015 | 620 | 370 | 250 | 1046 | 69 | 1644 |
| 2016 | 900 | 500 | 400 | 1118 | 69 | 1350 |
| 2017 | 1000 | 600 | 400 | 1158 | 73 | 1335 |
义乌市建筑垃圾产生量预测结果的准确度也依赖于原始数据的精确程度,仔细分析2008-2017年度义乌市建筑业相关经济数据表1,可以发现义乌建筑垃圾Y总、Y直和Y后3项原始数据在2013年前后数据变异性较大,是因为2013年开始义乌实施道路大规模改造、三改一拆、五水共治,2015年开始房屋去库存,大力发展房地产,2016年城市有机更新,导致城市建筑垃圾中间几年增长突变,2013年以前的数据参考意义不大,进行灰色预测的时候,选择2013-2017年共5年数据作为建立灰色预测模型信息更符合实际。
设2013-2017年义乌建筑垃圾Y总、Y直和Y后3项原始数据的建模序列分别为:
Y总(0)=(236,430,620,900,1000)
Y直(0)=(130,251,370,500,600)
Y后(0)=(106,179,250,400,400)
数据分析还表明:2013-2017年期间义乌建筑垃圾产量系统的行为数据受到扰动项的干扰,为了能够提高预测精度,在预测分析时,应构造弱化算子,这样经过扰动项的干扰会使数据的发展趋势变缓或振荡序列的振幅变小,弱化发展趋势,消除冲击扰动项的干扰,使失真的数据恢复其本来面目。
为了能够取得符合精度要求的的预测结果,构造弱化算子进行2阶弱化,得出弱化序列数据,利用弱化后数据序列建立灰色模型。
对2013-2017年义乌建筑垃圾Y总、Y直和Y后3项原始数据进行2阶弱化详细过程如下:
设原始数据序列
![]()
令![]()
其中![]()
式中D是一阶平均弱化缓冲算子
随后进行二阶弱化处理如下:
令![]()
其中![]()
式中D2是二阶平均弱化缓冲算
利用上述弱化算子对原数据序列进行弱化计算,Y总、Y直和Y后三项原始数据2级弱化后数据取整,用于灰色建模的数据序列分别表示如下:
Y总(0)D2=(833,882,930,975,1000)
Y直(0)D2=(488,518,547,575,600)
Y后(0)D2=(345,364,383,400,400)
2.2 构建灰色模型并进行义乌市建筑垃圾预测
义乌市建筑垃圾总数Y总预测建模步骤如下:
(1)Y总(0)D2=(833,882,930,975,1000)作AGO运算(一次累加生成,是为了更进一步发掘数据规律)得到:
Y总(1)=(833,1715,2645,3620,4620)
(2)构造矩阵B和YN
B=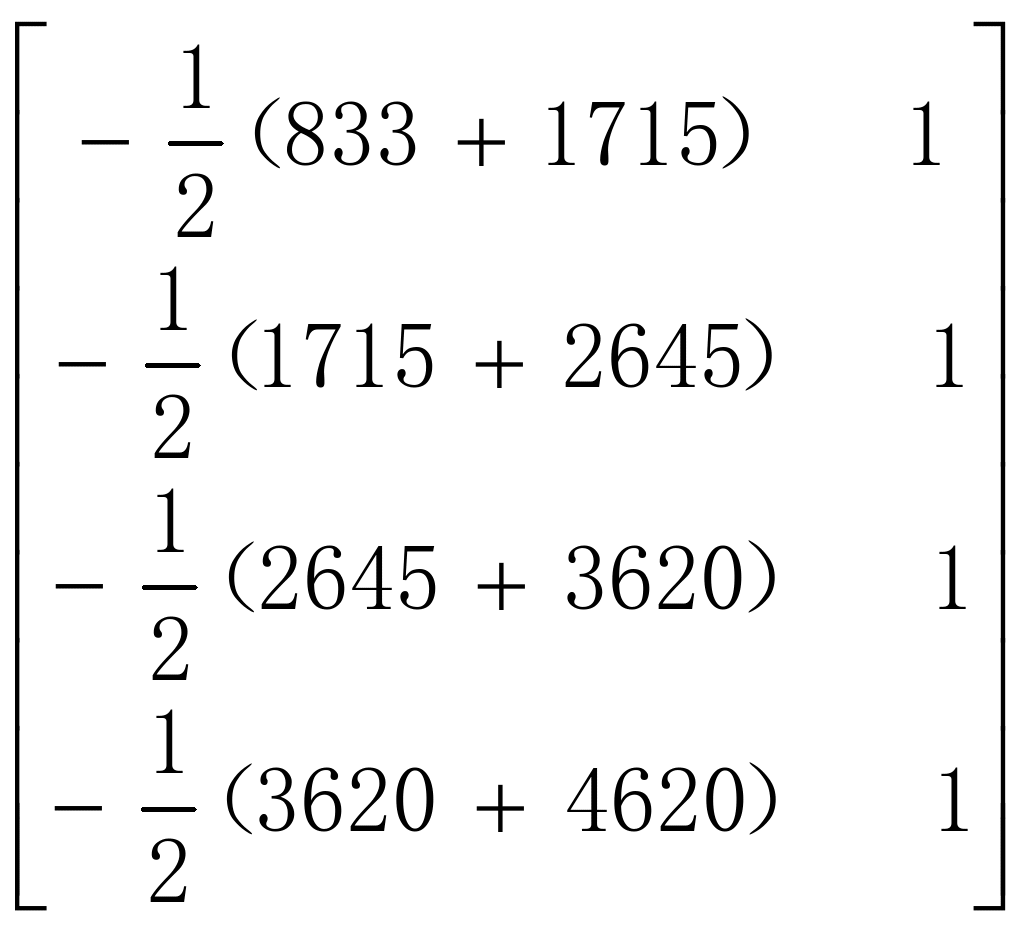 =
=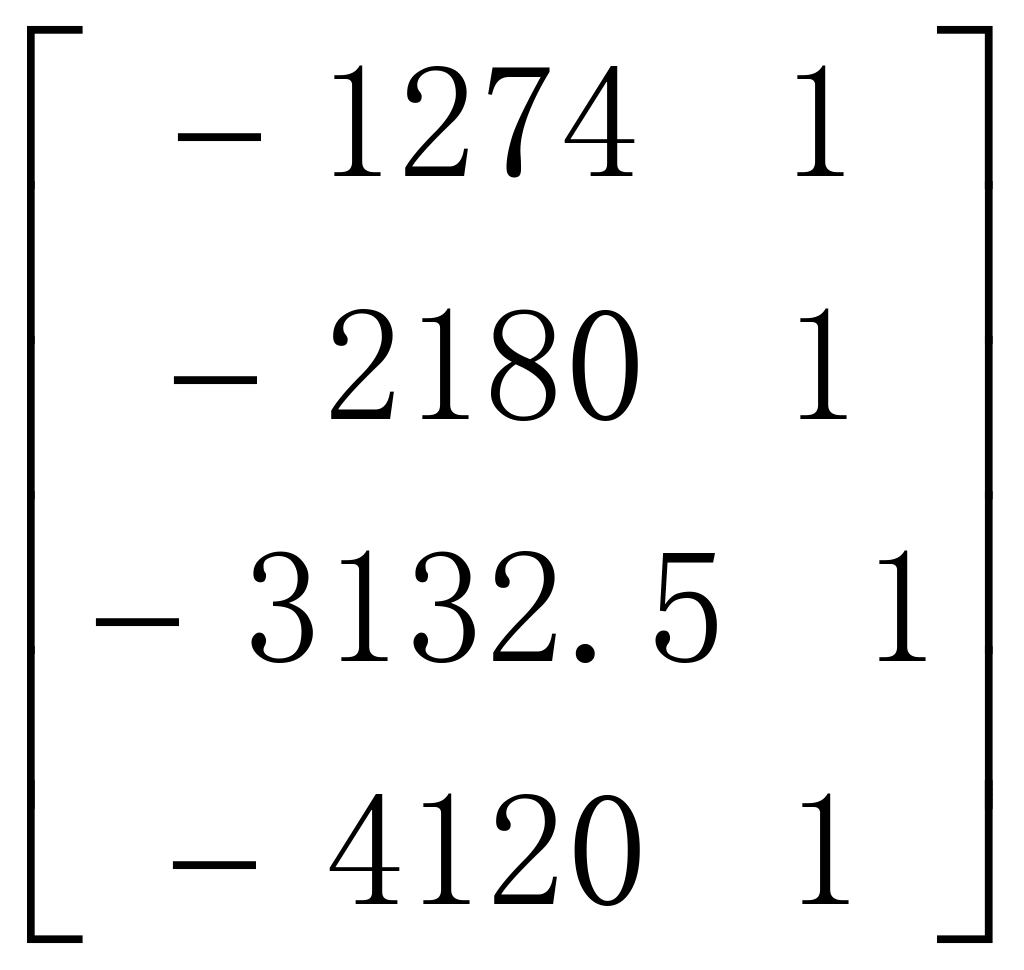 YN=
YN=![]()

(3)计算![]() (BTB)-1YN =
(BTB)-1YN =![]() =
=![]()
(4)![]() 总(1)(k+1)=
总(1)(k+1)=![]() =20739e0.042k-19906
=20739e0.042k-19906
(5)求导还原得:
![]() 总(0)(k+1)=-a
总(0)(k+1)=-a![]() =869e0.042k
=869e0.042k
同样方法,可以得到Y直和Y后的预测模型。Y总、Y直和Y后灰色预测模型及2018-2022年各自预测结果见表2。
表2 Y总、Y直和Y后灰色预测模型和预测值
| Y总 | Y直 | Y后 | ||
| 预测 模型 | 时间响应模型 | =20739e0.042k-19906 | =10381e0.049k-9893 | =11328e0.032k-10983 |
| 还原预测模型 | =869e0.042k | =507e0.049k | =362e0.032k | |
| 预测值 | 2018年 | 1050 | 632 | 418 |
| 2019年 | 1095 | 663 | 432 | |
| 2020年 | 1142 | 696 | 446 | |
| 2021年 | 1191 | 731 | 460 | |
| 2022年 | 1242 | 767 | 475 | |
| 相对误差α | 0.69% | 0.28% | 1.27% | |
2.3 灰色预测模型分析
(1)计算结果可看出,构建的义乌市建筑垃圾3个灰色模型发展系数-a分别为:0.042,0.049,0.032,均小于0.3,说明本模型适用于中长期预测[8]。所以采用本模型进行2018-2022年五年中期预测是可行的。
(2)灰色模型的精度一般常用相对误差α检验[8],经过2级弱化处理后的Y总、Y直预测模型预测相对误差α均小于1%,达到一级精度要求,Y后灰色预测模型的相对误差小于5%。达到二级精度指标要求,采用2阶弱化处理后的数据序列构建灰色模型,预测模型精度提高。
3 义乌市建筑垃圾三元回归分析模型的构建
3.1构建三元回归模型并进行义乌市建筑垃圾预测
影响建筑垃圾产生总量的因素很多,影响主要指标有:建筑施工面积、商品房销售面积、新开工面积、拆迁面积、GDP、居民收入、人口数量、政策影响、公共事件等。在建立预测分析模型时,选取过多的影响因素指标,会使模型参数不准确以至所建立的模型不可用。应根据影响大小和相关程度,把握关键指标,从而保证建立的预测模型可行[9]。根据左浩坤[10]用SPSS软件分析结论,选取义乌市GDP自变量x1 ,商品房销售面积自变量x2,建筑施工面积自变量x3,根据表1数据,采用SPSS软件Regression处理,构建关于Y总、Y直和Y后的三元线性回归方程分别为:
Y总=1.623x1+5.975x2-0.336x3-929 (3-1)
Y直=0.931x1+3.717x2-0.178x3-566 (3-2)
Y后=0.693x1+2.250x2-0.158x3-363 (3-3)
为了运用三元线回归模型预测义乌市2018-2022年的义乌Y总、Y直和Y后,先根据表1当中2008-2017年义乌市x1、x2、x3建立各自灰色模型,分别预测出2018-2022年义乌市x1、x2、x3各项数据,见表3。再利用三元线性回归方程(3-1),(3-2)和公式(3-3)可以分别计算2018-2022年义乌建筑垃圾Y总、Y直、Y后。数据见表3。
表3 2018-2022年义乌建筑垃圾三元回归预测数据表
| 年度 | Y总(万吨) | Y直(万吨) | Y后(万吨) | x1 (亿元) | x2 (万m2) | x3 (万m2) |
| 2018 | 1048 | 615 | 433 | 1241 | 81 | 1548 |
| 2019 | 1199 | 704 | 495 | 1317 | 88 | 1592 |
| 2020 | 1357 | 797 | 560 | 1398 | 95 | 1637 |
| 2021 | 1527 | 897 | 630 | 1483 | 103 | 1683 |
| 2022 | 1707 | 1004 | 703 | 1574 | 111 | 1730 |
3.2 三元回归预测模型检验
采用SPSS软件对以上3个三元线性回归方程进行检验。
(1)关于Y总、Y直和Y后的3个回归方程的拟合度R2分别为:0.910, 0.908,0.904,都接近于1,说明自变量y与因变量x1、x2、x3之间的线性关系密切,所建立的3个回归方程均具有较好的拟合程度
[11]。
(2)关于Y总、Y直和Y后的3个回归方程的显著性检验值F分别为:20.13,19.83,18.86。在显著性水平α=0.05的情况下,3个回归方程的 F >F0.05(3,6)=4.76。说明3个回归方程均是显著的[11]。
4 义乌市建筑垃圾灰色模型和三元回归分析模型预测结果对比分析
对比分析灰色预测表2和线性回归预测表3数据,两种模型预测结果差别较大。两个模型纵向数据对比看:线性回归模型预测数据增长幅度较大,而灰色模型预测数据较平缓。如回归模型预测义乌市建筑垃圾Y总2022年较之2017年增长幅度较大达到70.7%。灰色模型该项数据只有24.2%。回归模型和灰色模型横向数据对比看:2022年Y总分别为1707万吨和1242万吨,相差465万吨。从义乌市2018年后的各项建设综合分析,房地产开发平稳,城市有机更新也保持往年规模水平,三改一拆、五水共治等工程接近尾声,也没有其他重大的建设制度和项目出台,所以2018年后义乌市建筑垃圾产生量不会有较大幅度的增长,不会像前几年有突变性的增长幅度。这说明灰色模型预测的结果比较符合义乌市今后建筑垃圾增长的实际情况。统计回归分析模型的预测结果偏离了实际,也就是说统计回归分析模型不适合预测义乌市建筑垃圾的产生量。
究其原因,统计回归模型便于处理统计规律中较典型的概率分布,而对于非典型概率分布,非平稳过程的义乌市建筑垃圾产生量问题无法取得满意的预测效果。同时模型缺乏对义乌市建筑垃圾产生量系统结构和垃圾产生量机理的描述,掩盖了义乌市建筑垃圾产生量系统非线性、动态时变的特点,在这种基础上运用统计回归模型进行义乌市建筑垃圾产生量预测,其准确性自然无法满意。
5 结论
(1)对义乌建筑垃圾总量Y总、可直接利用量Y直、需处理后再利用量Y后3项原始数据序列构造弱化算子进行弱化处理,进行2阶弱化后更好地消除了数据的偏差,Y总、Y直模型达到一级精度,Y后模型的精度也到达二级精度。表明建模之前根据定性分析结论对原始数据序列施以缓冲算子,淡化或消除冲击扰动对系统行为数据序列的影响,对提高预测准确度有效果,但是高阶弱化是否对原始数据的内在规律有所改变需要更深入研究。
(2)通过建立建筑垃圾的灰色预测模型和三元线性回归模型预测2018-2022年义乌市建筑垃圾的相关数据,对比分析结果显示灰色预测更科学合理,精度高,有一定的实际参考价值,可以为建筑垃圾管理部门进行垃圾监管和提出垃圾利用对策提供依据。线性回归模型不适合做义乌市建筑垃圾预测。
(3)利用2008-2017年的义乌市GDP、商品房销售面积、建筑施工面积建立各自灰色模型,分别预测出2018-2022年各自对应数据,再用三元线性回归模型计算义乌市2018-2022 年义乌建筑垃圾总量、可直接利用量、处理后再利用量,这种线性回归模型和灰色模型结合使用,为线性回归模型预测提供了可信度较高的数据。
参考文献:
[1]张红玉,杨飞华.基于ARIMA模型的北京市朝阳区建筑垃圾产量分析与预测[J].环境工程.2014(1):696-699.
[2]巩柏含,呼国立,于洲洋.用多元线性回归分析建筑垃圾的低碳经济[J]金融经济,2015(2):158-160.
[3]周豪奇,张云宁,赵杰.基于灰色预测模型GM(1,1)的建筑垃圾产量研究[J].武汉理工大学学报,2016(5),612-615.
[4]王秋菲,王盛楠,石丹.基于灰色理论的建筑垃圾产生量的预测研究[J].沈阳建筑大学学报(社会科学版),2015(5):518-523.
[5]李亚东,龚志起,陈柏昆.基于灰色理论的西宁市建筑垃圾产量预测研究[J]青海大学学报,2017(6):82-87.
[6]公报-义乌市总务公开平台[EB].http://www.yw.gov.cn/.2018-07-03.
[7]楼森宇.义乌市资源节约和综合利用领导小组办公室“义乌市建筑垃圾资源化利用普查”课题研究报告,2016.
[8]刘思峰,谢乃明.灰色系统理论及其应用[M].北京:科学出版社,2008.
[9]许元,李聪.城镇建筑垃圾量的多元线性回归分析[J].砖瓦,2015(09):8-10.
[10]左浩坤,付双立.北京市建筑垃圾产生量预测及处置设施建设分布研究[J].环境卫生工程,2011,19(02):63-64.
[11]杨永愉,李志强.概率论与数理统计[M].北京:化学工业出版社,2008.
作者简介:舒怀珠(1968-);男;湖北黄冈人;高级工程师;硕士;主要从事土木工程灰色理论研究。
基金项目:浙江省住房和城乡建设厅2018年建设科研项目
项目编号2018K060
9