河南省濮阳市第一高级中学 (河南省 濮阳市 457000 )
在解题过程中常用“特例法探路,再作一般性的证明”这一解题策略,特例法探路是从特殊问题的研究中,拓宽解题思路,发现解答原题的方向和途径,为探究指明了方向,以便有效的避免解题的盲目性,可谓“拨开云雾见月明”,大致思路是先特殊探究,经过大胆猜想,再验一般,下面让我们一起逐个感悟!
例1、已知函数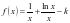 .(1)若函数
.(1)若函数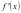 在区间
在区间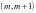 上有零点,求实数
上有零点,求实数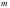 的取值范围;(2)若
的取值范围;(2)若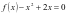 有实数解,求
有实数解,求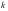 的取值范围.
的取值范围.
解析:(1)因为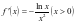 ,当
,当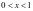 时,
时,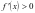 ,当
,当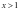 时,
时,
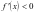 ,且
,且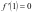 ,所以
,所以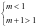 ,故得
,故得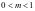 ;(2)将方程中的参数
;(2)将方程中的参数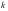 分离后,转化为求函数值域问题,则
分离后,转化为求函数值域问题,则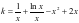 ,构造函数
,构造函数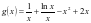 ,则
,则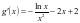 ,此时令
,此时令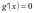 不易解,特殊值猜根,注意到
不易解,特殊值猜根,注意到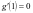 ,当
,当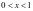 时,
时,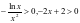 ,故
,故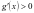 ,
,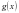 单调递增;当
单调递增;当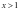 时,
时,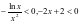 ,
,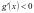 ,故
,故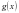 单调递减,所以
单调递减,所以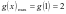 ,当
,当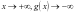 ,所以
,所以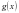 的值域为
的值域为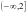 ,故实数
,故实数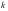 的取值范围为
的取值范围为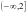 .
.
反思:将方程中的参数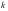 分离后,转化为求函数值域问题,这种方法是处理方程有解问题的最常用的方法,关于
分离后,转化为求函数值域问题,这种方法是处理方程有解问题的最常用的方法,关于 的方程
的方程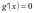 不易解,所以可用特殊值猜根,猜得
不易解,所以可用特殊值猜根,猜得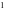 为方程的一个根,然后证明左右导数值一正一负,从而求出
为方程的一个根,然后证明左右导数值一正一负,从而求出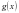 的最大值,也就求出了
的最大值,也就求出了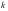 的取值范围.
的取值范围.
例2、已知正项数列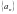 的前
的前 项和为
项和为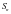 ,且
,且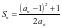 ,试求
,试求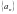 的通项公式.
的通项公式.
解析:本题若直接使用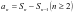 ,则会出现式子复杂,难以求解,下面我们调整方向,先看特例,当
,则会出现式子复杂,难以求解,下面我们调整方向,先看特例,当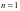 时,由已知得
时,由已知得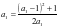 ,解得
,解得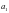
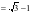 ,当
,当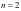 时,由已知得
时,由已知得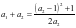 ,将
,将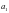
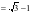 代入并整理得
代入并整理得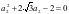 ,解得
,解得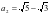 ,同理可得
,同理可得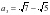 ,猜想
,猜想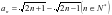 ,证明如下:首先当
,证明如下:首先当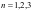 时,由上面推导可得通项公式成立,假设当
时,由上面推导可得通项公式成立,假设当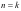
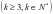 时,通项公式成立,即
时,通项公式成立,即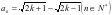 ,由于
,由于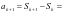
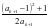
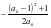
把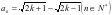 代入上式,整理得
代入上式,整理得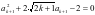 ,解得
,解得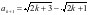 ,即
,即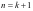 时通项公式成立,综上可知对所有
时通项公式成立,综上可知对所有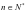 ,
,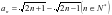 都成立.
都成立.
反思:本题通过观察有限个特例,猜想出一般性的结论,然后用数学归纳法证明,这种方法在解决探索性问题、存在性问题或与正整数有关的命题中有着广泛的应用.其关键是归纳、猜想出公式,基本步骤是试验、归纳、猜想、证明.
例3、已知椭圆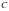 :
: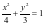 ,过右焦点
,过右焦点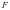 且斜率不为
且斜率不为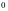 的直线和椭圆交于
的直线和椭圆交于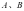 两点,
两点,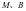 两点关于原点对称,直线
两点关于原点对称,直线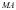 、
、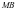 交直线
交直线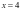 于
于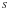 、
、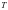 两点,记
两点,记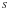 、
、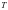 两点的纵坐标为
两点的纵坐标为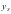 、
、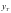 ,试问
,试问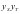 是否为定值,若是求出定值;若不是,说明理由.
是否为定值,若是求出定值;若不是,说明理由.
解析:常规思路是设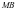 方程,求出点
方程,求出点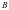 坐标,求出
坐标,求出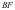 方程,求出点
方程,求出点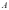 坐标,从而求出
坐标,从而求出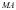 、
、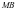 的方程,再求出
的方程,再求出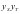 ,运算量大,计算繁琐.换个角度看问题,首先,利用特殊位置找出定值,再验证一般情况.当
,运算量大,计算繁琐.换个角度看问题,首先,利用特殊位置找出定值,再验证一般情况.当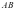 垂直于
垂直于 轴时,取
轴时,取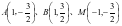 ,这时很容易求出
,这时很容易求出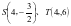 ,所以
,所以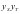
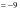 ,定值出现了,这就为我们证明一般情况增强了信心.设
,定值出现了,这就为我们证明一般情况增强了信心.设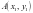 、
、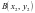 、
、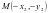 ,则
,则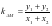 ,
,
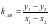 ,故
,故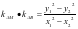 ,又因为
,又因为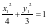 ,
,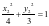 两式相减并化简得
两式相减并化简得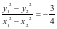 ,所以
,所以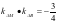 ,又因为
,又因为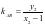 ,所以
,所以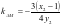 ,又
,又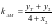 ,解之得
,解之得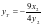 ,同理可求
,同理可求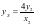 ,
,
所以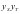
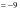 .
.
反思:本题是通过特殊位置猜想出定值,为证明提供了方向,又利用设而不求探求了直线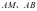 的斜率关系,利用点在曲线上找出定值,从而看清问题本质,高效的解决了问题.
的斜率关系,利用点在曲线上找出定值,从而看清问题本质,高效的解决了问题.
例4、已知椭圆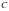 :
: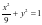 ,直线
,直线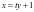 与椭圆
与椭圆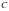 交于
交于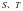 两点,椭圆的左右顶点分别为
两点,椭圆的左右顶点分别为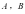 ,直线
,直线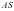 与
与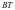 交于点
交于点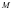 ,证明:当
,证明:当 变化时点
变化时点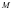 是否恒在一条定直线上,若是,求出该直线的方程,若不是,请说明理由.
是否恒在一条定直线上,若是,求出该直线的方程,若不是,请说明理由.
解析:先特殊探路,取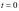 ,得
,得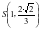 ,
,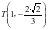 ,则直线
,则直线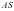 的方程为
的方程为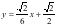 ,直线
,直线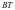 的方程为
的方程为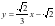 ,此时求得两直线交点
,此时求得两直线交点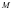
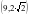 ;或取
;或取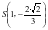 ,
,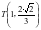 ,由对称性可知此时交点
,由对称性可知此时交点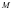
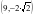 ,则可猜想点
,则可猜想点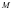 在定直线
在定直线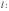
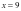 上,然后再证明对于任意的
上,然后再证明对于任意的 ,直线
,直线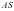 与
与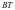 的交点
的交点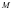 均在直线
均在直线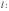
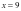 上.联立方程组
上.联立方程组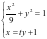 ,化简可得
,化简可得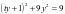 ,即
,即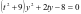 ,设
,设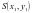 ,
,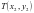 ,则
,则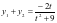 ,
,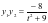 ,设直线
,设直线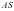 与直线
与直线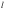 交于点
交于点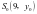 ,由斜率公式可得
,由斜率公式可得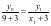 ,化简得
,化简得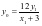 ;设直线
;设直线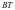 与直线
与直线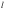 交于点
交于点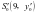 ,由斜率公式得
,由斜率公式得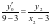 ,化简得
,化简得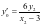 ;则
;则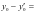
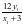
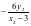
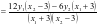 ,结合
,结合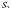
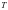 两点在直线
两点在直线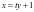 上,
上,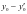
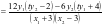

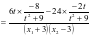
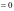 ,所以
,所以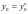 ,点
,点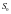 和点
和点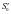 重合,这说明对于任意的
重合,这说明对于任意的 ,直线
,直线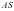 与
与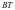 的交点
的交点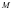 均在直线
均在直线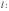
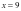 上,综上可知:当
上,综上可知:当 变化时点
变化时点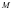 恒在定直线上,直线方程为:
恒在定直线上,直线方程为: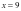 .
.
反思:本题着重考察对解题思路的探究,如果机械的套用求轨迹的方法进行解题,将陷入复杂运算的泥潭,使问题复杂化,而且很难得出正确结论,我们采用了特殊探路、大胆猜想、严格证明的解题思路,使问题峰回路转,柳暗花明.