《椭圆与标准方程》教学设计

黄港

湖南科技大学 422000

摘要：本节课选自《普通高中课程标准实验教科书（选修2-1）数学》（北师大版）第三章1.1节。本节内容作为“圆锥曲线与方程”的第一节内容，对高中数学学习具有承上启下的作用。在此之前，学生已经学习了圆的定义，由此可从圆的方程的探究方式出发，利用坐标法以及数形结合、转化化归的数学思想与方法，来研究椭圆的标准方程，从感性认识逐步上升为理性认识，从而理解椭圆这一概念的本质。

关键词：圆 椭圆 坐标法 数形结合

教学目标：

1. 知识与技能：（1）掌握椭圆的定义；（2）理解并掌握椭圆及其标准方程的代数表达。

2. 过程与方法：（1）掌握椭圆标准方程的建立与推导；（2）体会数形结合以及转化化归等数学思想方法的运用。

3. 情感态度与价值观：通过探究学习，激发学习兴趣，提高学习积极性与主动性，体会利用数学知识解决问题。

教学重点：

椭圆的定义以及标准方程的应用。

教学难点：

对椭圆定义的理解以及椭圆标准方程的建立与推导。

教学过程：

1. 折纸游戏，创设情境

师：请每一组同学拿出准备好的圆纸片，找出圆心A点，以及另一点B点，翻折圆周，使得折过来的圆弧始终过B点，并将折痕用笔画出。哪组画的折痕越多哪组获胜。开始游戏！（用几何画板展示游戏规则与结果）

【设计意图：通过设置的竞争游戏激发学生积极性与主动性，提高课堂趣味性，引导学生发现问题：圆中有一个椭圆区域没有任何折痕。通过几何画板进行游戏规则展示与结果展示，化抽象为具体，引导学生思考探究。对于游戏结果提出疑问，激发学生的好奇心。】

2. 导入新课，探索新知

师：同学们，椭圆的形状就好像是一个“小胖子”不小心把圆坐扁之后的样子，那我们今天不妨从研究圆的方法来研究椭圆！

（一）播放教师用绳和图钉画圆与画椭圆视频。

师：同学们，画圆需要确定圆心，即图钉的位置，以及半径，即绳子长度，那么画椭圆需要确定哪些条件呢？

师：如果改变两个图钉的位置，固定绳长，画出来的图形还会是椭圆吗？

师：（用几何画板进行演示）请同学们观察其变化规律，并做出总结。

PPT展示：绳长记为2a，两定点间的距离记为2c (c≠0).

1、当2a>2c时，轨迹是 椭圆 ；

2、当2 a =2c时，轨迹是以F₁ ,F₂为端点的线段；

3、当2 a <2c时，无轨迹。

（二）展示椭圆定义

定义：平面内到两个定点F₁ ,F₂的距离之和等于常数（2a）（大于| F₁ F₂|）的点的轨迹叫椭圆^[3]。

定点F₁ ,F₂叫做椭圆的焦点。两焦点之间的距离叫做焦距（2c）。

椭圆上相距最远的两点之间的连线为椭圆的长轴。

椭圆上相距最近的两点之间的连线称为椭圆的短轴。

（三）探索椭圆方程

1、介绍勒内·笛卡尔，皮埃尔·德·费马两位数学家，引出其研究思想：通过坐标法与数形结合思想，将图形的性质用代数形式表示，从而得出方程。

2、回顾“圆的方程”的推导，利用建系、设点、限制、代入、化简的步骤求解，并利用“建设现代化”的口诀进行记忆。

3、探讨建立平面直角坐标系的方案

师：我们发现，当以椭圆的中心为坐标原点，直线F₁ ,F₂ 为x轴（方向向右），线段F₁ ,F₂ 的垂直平分线为y轴（方向向上），建立直角坐标系时，建立的平面直角坐标系最简单。

4、学生利用口诀进行探究求解

要求：

（1）建系：当以椭圆的中心为坐标原点，直线F₁ ,F₂ 为x轴（方向向右），线段F₁ ,F₂的垂直平分线为y轴（方向向上），建立直角坐标系^【1】。

（2）设点：设P (x, y)是椭圆上任意一点，椭圆的焦距| F₁ F₂ |=2c(c>0)，

则F₁ ,F₂的坐标分别是(c,0)、(c,0) .

P与F₁ 和F₂的距离的和为固定值2a(2a>2c)。

（3）限制：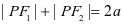

（4）代入：代入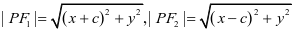 ，得到方程： 。

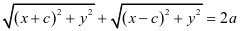（5）化简： 。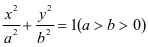

5、探究焦点在y轴上的椭圆标准方程。

6、学生交流，教师归纳总结椭圆标准方程的特点。

（1）椭圆标准方程的形式：左边是两个分式的平方和，右边是1。

（2）椭圆的标准方程中三个参数a、b、c满足a²=b²+c²。

（3）由椭圆的标准方程可以求出三个参数a、b、c的值。

（4）椭圆的标准方程中，x²与y²的分母哪一个大，则焦点在哪一个轴上^[2]。

【设计意图:用类比的思想，由圆的研究方式来研究椭圆，利用数形结合、划归与转化等的数学思想方法，激发学生学习欲望，引导学生主动探究，以多种形式逐个攻破教学难点，引导学生“在做中学”。】

3. 课堂总结，强化新知

由学生进行抢答活动，完成下表:

【设计意图：通过图表的形式，及时巩固所学知识，促使学生更加直观地掌握学习内容，通过找相同点与不同点，使学生对知识学习更加深入；通过学生抢答，提高学生的竞争意识，以及学习积极性与主动性。】

4. 小试牛刀，巩固新知

例题1. 已知椭圆的方程为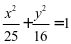： ，请填空：

1. a= 5 ，b= 4 ，c= 3 。

2. 焦点坐标为 (-3,0) 、 (3,0) ，焦距等于 6 。

3. 若C为椭圆上一点，F₁、F₂分别为椭圆的左、右焦点，并且CF₁= 2 ,则 CF₂= 8 。

例题2.求适合下列条件的椭圆的标准方程：

(1)a=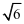 ,b=1,焦点在x轴上；

(2)焦点为F₁(0,－3)，F₂(0,3),且a=5；

(3)两个焦点分别是F₁(－2,0)、F₂(2,0),且过P(2,3)点。

师生分析：根据已知条件进行分析，总结求椭圆标准方程的解题步骤：

（1）确定焦点的位置；

（2）设出椭圆的标准方程；

（3）根据题目条件确定a、b的值，写出椭圆的标准方程。

【设计意图：通过典型例题的讲解与分析，使学生掌握基本的解题能力；通过练习及时巩固知识，加深学生对于椭圆性质的理解。】

五．课后探究

师：同学们现在可以了解上课开始时玩的游戏的奥秘了吗？（利用几何画板展示游戏原理）

【设计意图：通过本节课的学习，解答游戏原理，使学生亲身体验通过学习解决问题的过程】

参考文献

[1]舒林军, 蒋志明, 沈联晖. 《高考数学备考随身酷》浙江教育出版社 ISBN：7-5338-5527-2 2004-09-01

[2]史文照 《新课程·下旬》ISSN：1673-2162 ISSN：1673-2162

[3] 徐州名师编写组《新课标高中数学：选修1-1》北京大学出版社 ISBN：7-301-11170-3 2006-11-01