灰色 IDGM(1,1)模型在地表沉降预测中的应用

灰色 IDGM(1,1)模型在地表沉降预测中的应用

张立城 陈勇 吕旭 刘泉 郭钦 周二雷

中国十七冶集团有限公司 安徽 马鞍山   243000

摘要：灰色预测模型具有所需样本少，计算流程简便等特点广泛运用在地表沉降预测领域中。针对传统的GM（1,1）灰色预测模型固有模型的不足，为了满足地表沉降预测精度要求，本文提出使用近似非齐次指增长序列的间接模型-IDGM（1,1）模型，该模型弥补了传统灰色模型针对近似非齐次指增长序列的模拟性能不理想的问题。结合工程实例表明，IDGM（1,1）利用已获得观测数据能够更好的预测未来一段时间内地表沉降量，可以为安全施工提供有力依据。

关键词：沉降预测；IDGM(1,1)；基坑；灰色理论

0 引言

基坑周边地表沉降观测作为监测基坑施工变形安全的措施，地表沉降观测可以非常有效的反应出基坑周边土体乃至基坑支护变形的情况，在整个地下空间工程施工中显得尤为重要。近年来，国内许多学者针对各种土质、各种工况条件下的土体变形预测做过大量的探索。刘念武等，研究了软土深开挖周边土体的变形特征^[1]。宋楚平利用BP神经网络探索预测方法^[2]。孙曦源等针对地铁车站基坑施工提出了经验预测法^[3]。胡之锋等，对黏土层的土体变形预测做了深入的探讨及研究^[4]。这些方法可以对基坑周边土体变形进行很好的预测。灰色理论经过40年的发展，已经成为一套具有很强实用性的数学体系，并且广泛的运用在各行各业。对于基坑周边地表沉降预测，灰色利用具有所需样本少，计算方便简单等优点，便于工程人员在施工现场使用。

1 模型建立流程^[10]

灰色近似非齐次指增长序列的间接预测模型的具体建模流程如图所示。

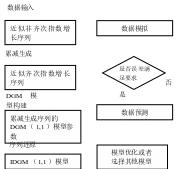
2 IDGM（1,1）模型^[9]

2.1灰色模型建立^[10]

设原始序列为

Error: Reference source not found ,

其中 ， 为 的一次累减序列，即

为非负数序列，其中一次累加生成序列为

其中，

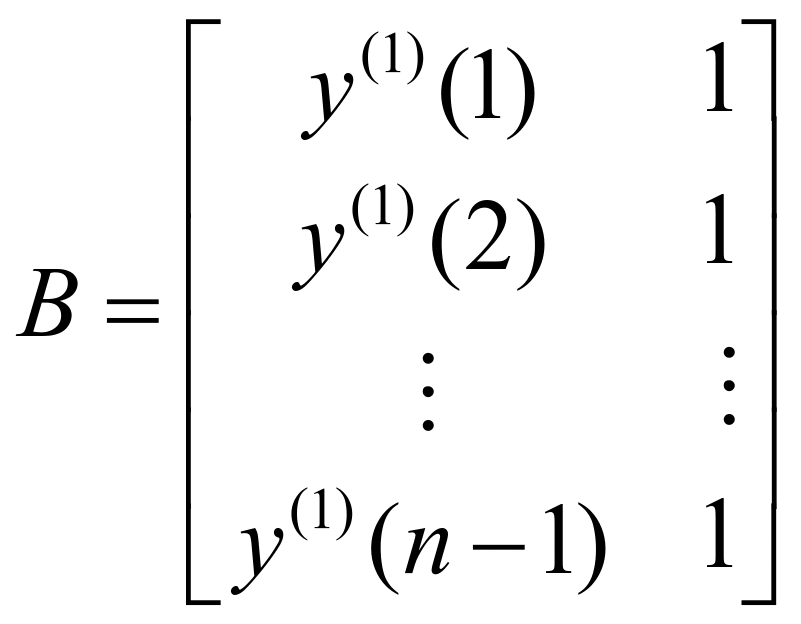
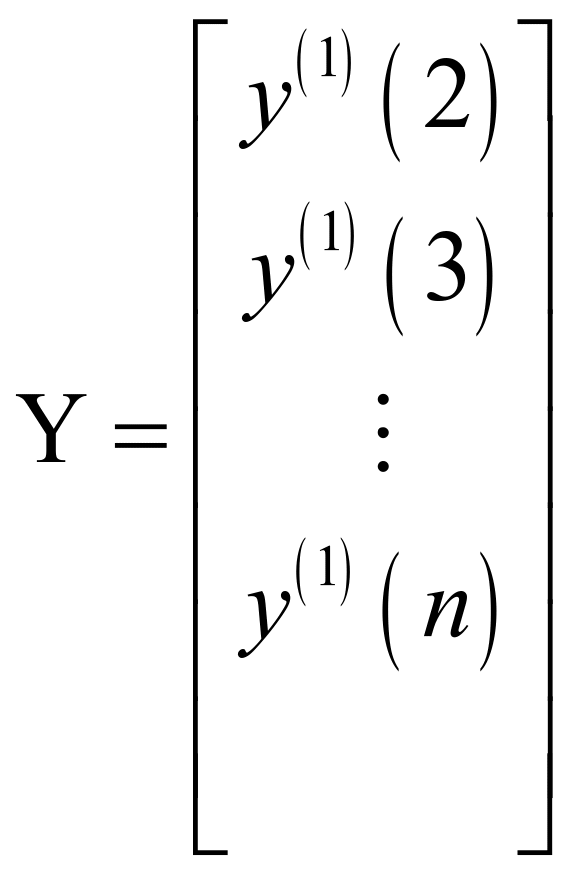
则，

取 则，

(1)

其累减还原式为，

(2)

设，

，

则， (3)

(4)

推出IDGM的表达式为，

(5)

3工程实例

3.1工程概况

马鞍山市智慧小镇配套服务中心项目位于慈湖高新区笔架山路以北，雨佳路以南，建设总建筑面积73819㎡，其中包含1栋12层研发楼、13层人才公寓、13层商务酒店及12栋3层总部办公，容积率1.74，绿地率31.5%，建筑密度29.9%。

3.2分析预测

为了保证预测的准确性以及评估IDGM（1,1）的预测性能，选取该工程周边地表沉降两个观测点1号与2号的等时距12期监测数据带入GM（1,1）与IDGM(1,1)模型中，其中前10期数据作为原始数据，后2期数据作为预测性能评价数据。

将表1、表2的数据分别带入传统GM（1,1）模型与IDGM（1,1）模型进行拟合预测计算。

传统GM（1,1）模型与IDGM（1,1）模型针对1号和2号测点的拟合值及预测值如表3、表4所示。

为了更加直观的比对出两种模型的预测性能，将拟合预测值与原始值的残差及相对误差绘制成散点图，如图1-4所示。

表1 1号测点沉降数据

由图1-4可知，不论是1号测点还是2号测点，利用IDGM（1,1）模型所拟合及预测的地表沉降量的残差及相对误差均小于GM（1,1）模型。IDGM（1,1）模型的散点分布更接近坐标轴，预测性能更好。

由表1可知，1号测点的IDGM（1,1）模型预测值与原始值的最大残差为0.026，最大相对误差为，0.79%。而GM（1.1）模型的残差与最大相对误差分别为0.367和5.75%远高于IDGM（1,1）模型。

由表2可知，2号测点的IDGM（1,1）模型预测值与原始值的最大残差为0.029，最大相对误差为，1.25%。而GM（1.1）模型的残差与最大相对误差分别为0.146和6.89%也远高于IDGM（1,1）模型。

表2 2号测点沉降数据

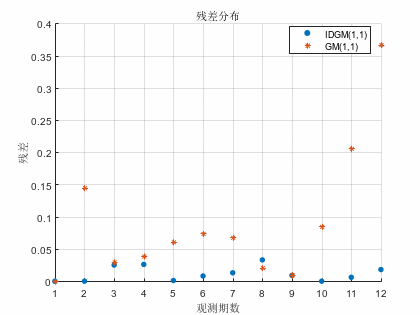
图1 1号测点两种模型测点残差分布图

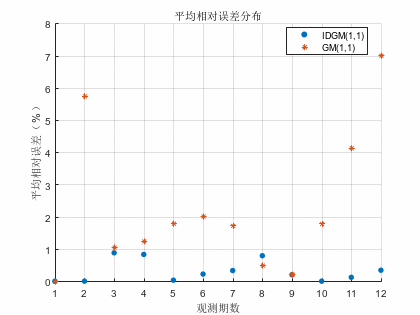
图2 1号测点两种模型相对误差分布图

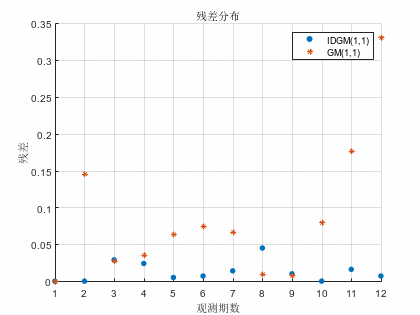
图3 2号测点两种模型残差分布图

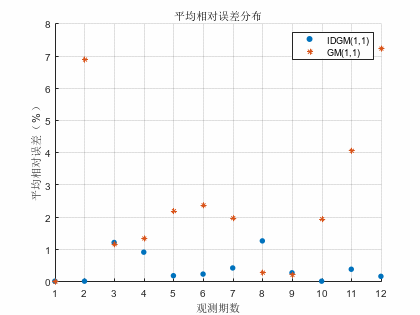
图4 2号测点两种模型相对误差分布图

表3 1号测点不同模型拟合预测值

表4 2号测点不同模型拟合预测值

4 结论

1)IDGM(1,1)模型通首先利用原始序列的累减数列生成再次累加数列，再进行反向数据还原，相比于传统GM（1,1）模型具有更好的预测精度及预测性能。

2)IDGM(1,1)模型建模简单，预测所需样本数量少，计算方便简单，便于工程人员在施工现场使用。

参考文献：

1. 刘念武,陈奕天,龚晓南,俞济涛.软土深开挖致地铁车站基坑及邻近建筑变形特性研究[J].岩土力学,2019,40(04):1515-1525+1576.

2. 宋楚平.一种改进的BP神经网络深基坑变形预测方法[J].土木工程与管理学报,2019,36(05):45-49+55.

3. 孙曦源,衡朝阳,周智,张剑涛.厦门地铁车站基坑施工诱发地表沉降的经验预测方法研究[J].土木工程学报,2019,52(S2):132-138.

4. 胡之锋,陈健,邱岳峰,李健斌.一种黏土层中深基坑开挖地表沉降预测方法[J].长江科学院院报,2019,36(06):60-67+72.

5. 刘伟,吴新宇,彭海燕.不同开挖顺序下软土深基坑受力与变形对比分析[J].工程质量,2019，37(06):19-25

+32.

6. 王晓曙,张延杰,高嘉丽,王锐麟,高春雷.南昌某地铁深基坑施工对周围地表沉降的影响因素分析[J].施工技术,2018,47(S4):1398-1401.

7. 邓聚龙.灰色预测与决策[M].武汉:华中科技大学出版社，2002.

8. 谢乃明, 刘思峰. 离散 GM (1, 1) 模型与灰色预测模型建模机理[J]. 系统工程理论与实践, 2005, 25(1): 93-99.

9. 曾波,刘思峰.近似非齐次指数增长序列的间接DGM(1,1)模型分析[J].统计与信息论坛,2010,25(08):30-33.

10. 刘思峰, 党耀国, 方志耕, 等.灰色系统理论及其应用[M].5版.北京:科学出版社,2010:176−17.

作者简介：张立城（1990-02），男，汉族，籍贯：河北省黄骅市，当前职务：副总工程师，当前职称：助理工程师，学历：本科，研究方向：工程技术