基于数值模拟的螺栓连接预紧力分析

基于数值模拟的螺栓连接预紧力分析

潘铖凌

南京康尼机电股份有限公司轨道事业总部技术中心 江苏南京 210013

摘要：为了对关键螺栓连接提供准确的预紧力，建立了螺栓连接三维有限元模型，对螺栓连接预紧过程进行了模拟仿真,得到了拧紧力矩和预紧力的关系曲线，和传统理论方法得到的曲线吻合较好，说明有限元数值模拟能够准确获得螺栓连接预紧力大小，为关键螺栓连接设计提供了理论依据。

关键词：螺栓连接；拧紧力矩；预紧力；数值模拟

1 引言

螺栓连结因其易于拆装而广泛应用于机械结构中。安装时必须拧紧螺母，以使在拉伸螺栓同时压缩被连接部件，这个螺栓预先受到的拉力称为预紧力。预紧的目的是加强连接的可靠性和紧密性，但预紧力过大会导致螺栓屈服甚至断裂，过小则可能导致被连接部件间松动导致连接失效^[1]。因此，合适的预紧力对螺栓连接非常重要。在装配过程中，预紧力测量比较困难，通常采用扭矩扳手来调节拧紧力矩。因此，确定拧紧力矩与预紧力之间的关系对于螺栓连接具有重要意义。

2 拧紧力矩和预紧力的关系

由机械设计手册可知^[2]，拧紧力矩T和预紧力F₀的关系为：

T=KF₀d （1）

上式中，d为螺纹的公称直径，mm；K为拧紧力矩系数，对于M10~M64粗牙普通钢制螺栓，K=0.1~0.3，通常取平均值K=0.2。

受接触面摩擦因子和螺纹副参数几何偏差的影响，在T一定时，F₀的离散性较高，无法准确预测F₀的大小，最大误差可达±40%^[3]，对关键螺栓连接的设计影响很大。因此，本文尝试利用有限元数值模拟预测拧紧力矩T和预紧力F₀之间的真实关系，以期获得准确的预紧力大小。

3 有限元数值模拟

3.1 有限元分析模型

有限元模型包含一个M12x50螺栓、螺母和一个被连接件，它是一个空心圆柱体，其内径13mm，外径39mm，如图1所示。

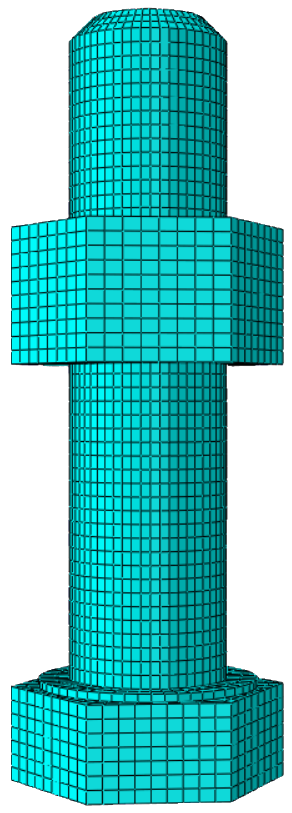
图1 螺栓连接有限元网格模型

考虑到接触分析要求及减少计算时间，采用六面体单元（C3D8R）进行网格划分^[4]，整个模型包含15888个单元，18623个节点。螺栓、螺母材料为42CrMo，弹性模量为206GPa，泊松比均为0.3；被连接部件材料为6082-T6，弹性模量为70GPa，泊松比为0.334。

模型中有以下几种接触：螺纹副间的接触，螺母和被连接部件间的接触，螺栓头部和被连接部件间的接触，定义接触行为属于小滑移，摩擦因子μ=0.15。

3.2 边界条件和载荷

限制螺栓头部底面边缘全部节点为固定。通过在六角螺母两个对应侧面施加大小相等、方向相反的表面分布力，将要施加的拧紧力矩加载到螺母上^[5]，如图2所示。拧紧力矩T=τSL，其中τ为均匀分布在螺母侧面的表面分布力，S为螺母侧面的面积，L为两侧面间的距离。本文目标拧紧力矩T为92Nm。

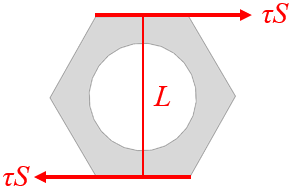
图2 在螺母上施加拧紧力矩

3.3 结果与讨论

通过有限元模拟得到了拧紧力矩T=92Nm时螺栓连接的应力分布云图，如图3所示。由图3判断出螺纹部分的最大应力出现在螺栓、螺母旋合开始位置，与螺栓连接的实际情况相符。在不同拧紧力矩下，进行模拟仿真，提取螺栓横截面上的预紧拉力F₀，得到拧紧力矩-预紧力曲线，如图4所示。拧紧力矩T=92Nm时，仿真分析得到预紧力F₀=40.3kN。

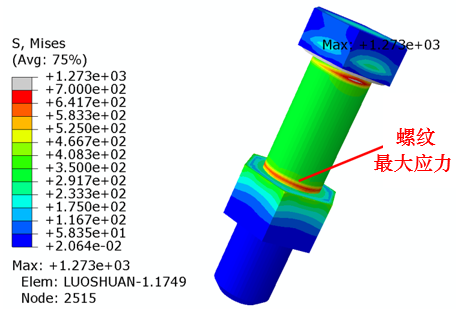
图3 螺栓连接应力云图

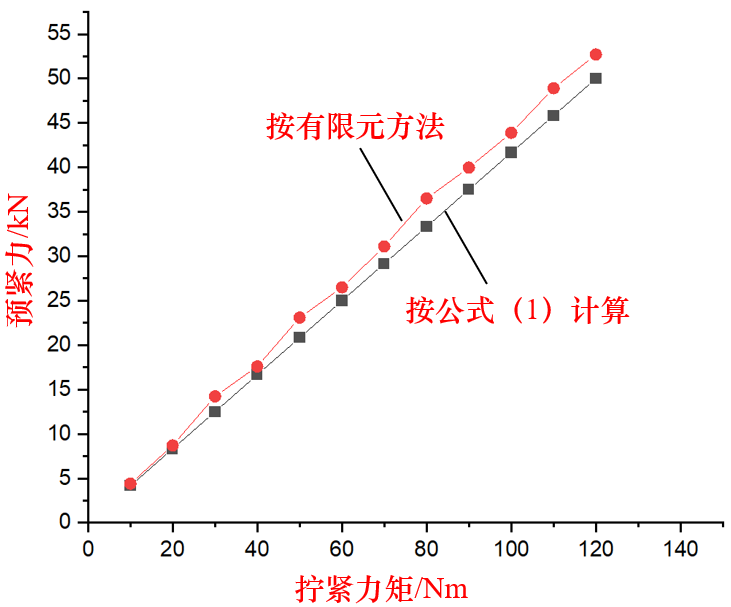
图4 拧紧力矩与预紧力关系曲线

由图4可知，基于有限元法的拧紧力矩与预紧力关系曲线和传统理论方法公式（1）得到的关系曲线是一致的，吻合程度较好。说明本文所采用的有限元分析方法能够准确地模拟螺栓连接的预紧过程和预紧力大小。

4 结束语

建立了螺栓连接三维有限元模型，对螺栓连接预紧过程进行了模拟仿真,得到了拧紧力矩和预紧力的关系曲线，该曲线和传统理论方法计算获得的曲线吻合较好，说明有限元数值模拟能够准确获得螺栓连接预紧力大小，为关键螺栓连接提供准确的预紧力提供了理论依据。

参考文献：

[1]濮良贵,陈国定,吴立言.机械设计(第九版)[M].北京:高等教育出版社,2013,5:68-70.

[2]成大先.机械设计手册[M].北京:化学工业出版社,2003.

[3]张振华,应秉斌,矫明.螺栓拧紧力矩的确定方法及相关探讨.化学工程与装备,2009,2:105-107+96.

[4] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2006.6:135-150.

[5]刘坤,刘文雨.基于ABAQUS的螺栓预紧分析.机械制造与自动化,2011,2:105-107.