陆军装甲兵学院士官学校
摘要:本文研究了基于卷积神经网络的超宽带通信系统室内密集多径信道模型识别。首先介绍了经典的超宽带室内密集多径信道模型,并对IEEE802.15.4a信道模型CM1~CM4这4种信道的冲激响应进行了仿真,进行为后续实现信道模型识别奠定了理论基础;随后本文提出了基于卷积神经网络对信道模型进行识别,针对不同的结构、不同的参数分别进行了试验,最终选择出较为合理的网络结构和参数,取得较好了效果。
关键词:卷积神经网络 超宽带 密集多径 信道识别
概述
随着超宽带通信系统应用越来越广泛,关于其信道模型的研究和测量也与时俱进,面对越来越多的不同场景的信道模型,传统的模型识别与参数估计方法不能很好适应新模型,识别和估计的针对性较差,准确率较低,这就为超宽带通信系统的设计和优化带来了一定的困难。
卷积神经网络作为常用的深度学习模型,其在特征提取方面具有极高的准确度,可以用于多分类问题,近年来得到广泛的关注和应用。与传统方法相比,其优势在于提取特征较为准确,分类精度高,且人为影响因素少;与其他神经网络相比,它最大的优点在于可以权值共享,从而大大降低了计算量,提高了网络效率。
超宽带通信系统密集多径信道模型
目前应用最广泛的超宽带密集多径信道模型是由Saleh和Valenzuela提出的,即S-V模型[6]。它具有簇和多径成分的概念,IEEE802.15.3a和IEEE802.15.4a模型[7]均是由该模型改良而来。这两个模型均是基于修正的S-V模型,在大量实测数据的基础上进行拟合,区分不同场景得到相应的信道模型。本文基于IEEE802.15.4a信道模型,选取其中信道复杂度较高的4种室内场景为研究对象。
表2-1 IEEE802.15.4a信道场景分类
信道编号 | 模型说明 |
CM1 | 室内视距传播居住环境(7~20m) |
CM2 | 室内非视距传播居住环境(7~20m) |
CM3 | 室内视距传播办公环境(3~28m) |
CM4 | 室内非视距传播办公环境(3~28m) |
通过仿真,分别取100个通道叠加得到的4种信道冲激响应如下图所示。
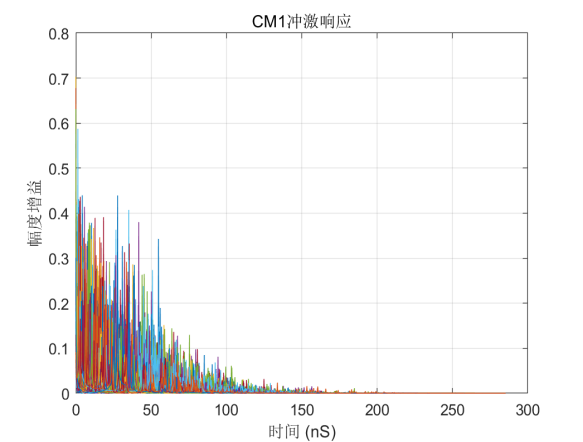
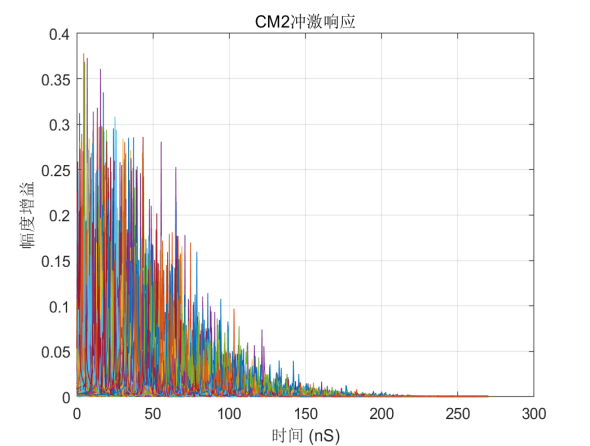
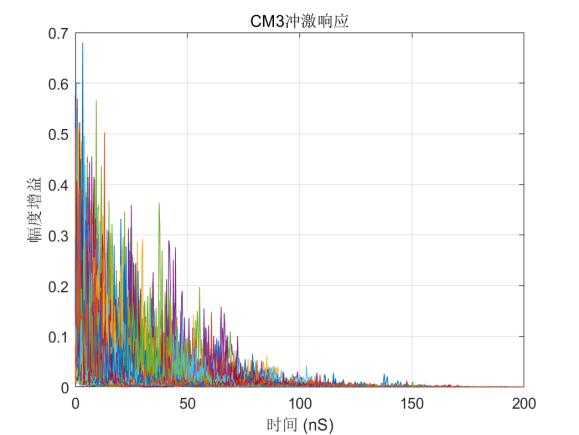
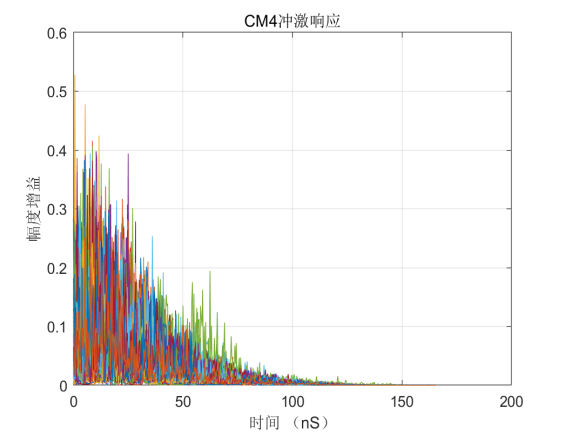
图2-1 IEEE802.15.4a信道4种场景冲激响应仿真
本文将超宽带接收信号经过预处理后获得的数据集样本为2502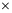 1
1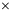 60400,数据集共分为4类,每类样本数为15100,由于卷积神经网络工具箱默认输入的数据集必须为四维数据,故对原250
60400,数据集共分为4类,每类样本数为15100,由于卷积神经网络工具箱默认输入的数据集必须为四维数据,故对原250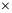 2
2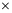 1
1 15100的数据集样本进行了升维。对于每一个接收信号矩阵来说,都可以视为是250
15100的数据集样本进行了升维。对于每一个接收信号矩阵来说,都可以视为是250 2的灰度图像。
2的灰度图像。
3、CNN模型设计及参数选取
3.1结构设计
表2-7为在不同网络深度下分类的准确率。实验中,输入的数据集完全相同,均为4种信道下每类样本数15100个,学习率为0.01,迭代100次,每层卷积层卷积核大小均为[3 1],卷积核个数均为30,激活函数为ReLU函数,池化层选择最大池化,卷积层与池化层数量相同、交替工作。由该表可以看出,在相同条件下,卷积神经网络深度越高,层数越多,其分类的准确率越高,并且在原层数越浅的情况下,每加深一层,测试准确率提高越显著。当网络层数相同时,增加卷积层对于准确率的提高效果比增加全连接层要显著。
表3-1 不同网络深度分类准确率
结构编号 | 卷积层数 | 全连接层数 | 测试准确率 |
1 | 2 | 1 | 63.58% |
2 | 3 | 1 | 87.62% |
3 | 2 | 2 | 64.12% |
4 | 3 | 2 | 93.63% |
基于以上实验,本文中设计的用于超宽带室内密集多径信道模型识别的卷积神经网络共包含10层:1个输入层、3个卷积层、3个降采样层,2个全连接层和1个输出层,其具体结构参数如表所示。
表3-2 卷积神经网络结构参数表
层序号 | 层类型 | 层参数 |
1 | 卷积层 | [3 1] |
2 | 池化层 | [3 1] |
3 | 卷积层 | [3 1] |
4 | 池化层 | [3 1] |
5 | 卷积层 | [3 1] |
6 | 池化层 | [3 1] |
7 | 全连接层 | 100 |
8 | 全连接层 | 4 |
3.2参数选取
神经元网络权值进行更新时,其系数称之为学习率。卷积神经网络的学习效果不仅与网络的结构有关,还与学习过程中的学习率和迭代次数等参数相关。根据已经调整好的网络结构,对不同的学习率和迭代次数进行实验,获取最佳参数。当迭代次数为5时,学习率的实验结果如表所示。
根据实验结果可以看出,在迭代次数相同的情况下,当学习率较小的时候,卷积神经网络的准确率比较高,当学习率大于0.6时,网络的准确率大幅下降,这说明在该学习率下,网络稳定性比较差,不能够较好的完成分类任务。这与选择的激活函数有关,当学习率较高时,部分神经元坏死,故而分类效果较差。同时,训练时间随学习率变化并不大,基本稳定在[33,34]之间,这说明学习率并不会影响训练时间,只会影响数据集的收敛。综合考虑训练时间和准确率,本网络的学习率确定为0.01。
表3-3 学习率与卷积神经网络特征提取准确率及时间的关系
学习率 | 准确率 | 训练时间 |
0.01 | 92.91% | 33s |
0.1 | 92.6% | 33s |
0.2 | 92.53 | 33s |
0.3 | 92.46 | 32s |
0.4 | 92.37% | 33s |
0.5 | 90.44% | 33s |
0.6 | 73.62% | 34s |
0.7 | 67.74% | 34s |
在已确定的网络结构下,当学习率为0.01时,迭代次数的实验结果如图3-1所示。当迭代次数为3次时,其训练准确率已经可以稳定在90%以上,说明该卷积神经网络在训练时收敛较快,得到的正确率比较高,网络结构设计和参数选取得比较合理。
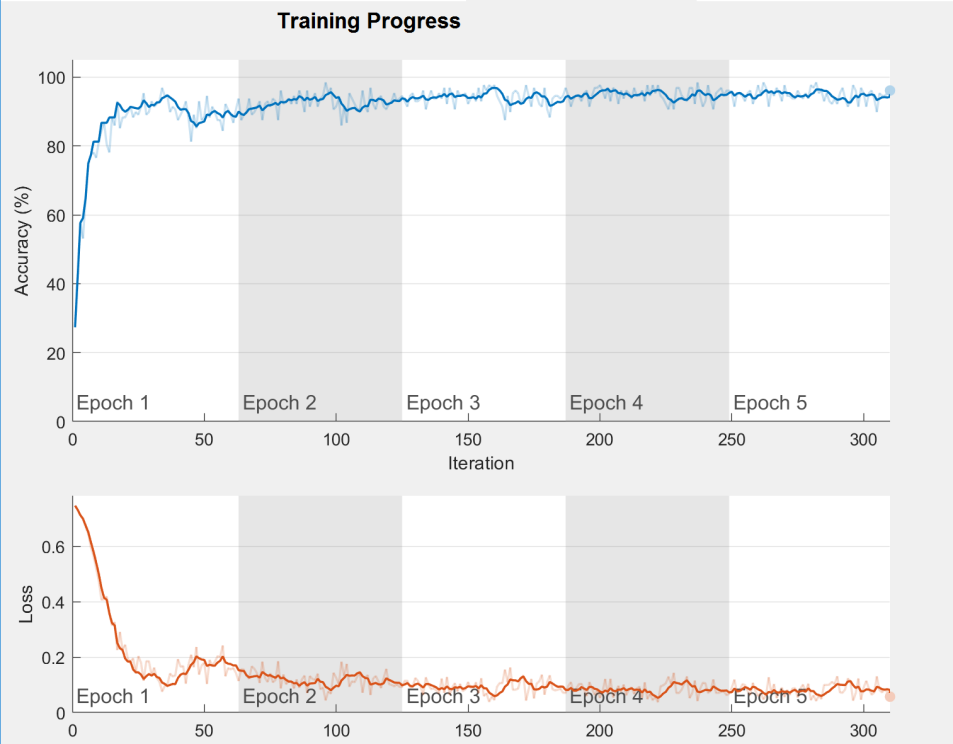
图3-1 迭代次数与卷积神经网络特征提取识别准确率的关系
4、仿真结果及与其他方法对比
选取训练集数量为15100 4、测试集数量为15100
4、测试集数量为15100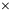 4的一组数据详细分析各类信道模型分类准确率,该网络训练的准确率为100%,测试准确率为93.63%,得到的分类结果如下图混淆矩阵所示。该矩阵纵轴为测试集样本的真实信道标签,横轴为经过卷积神经网络识别后得到的信道模型类别,每个方格中的数字为其所占的百分比,为确保分析结果精确,该矩阵中保留小数点后三位。由该矩阵图可以看出,CM2的识别准确率最高,为96.5%,CM4的准确率最低,为90.2%,并且CM1只会被错误的识别为CM2,而不会被识别为CM3或CM4,同样的,CM3只会被错误的识别为CM4,而不会被识别为CM1或CM2。之所以会这样,可以由表2-1得知,CM1和CM2均为室内居住环境,差别为是否为视距状态,因此,CM1和CM2的信道相似度比较高,与CM3或CM4的相似度比较低,故而提取后的特征差别较大。可见,卷积神经网络进行分类识别的结果及误差是与实际应用背景相符合的。
4的一组数据详细分析各类信道模型分类准确率,该网络训练的准确率为100%,测试准确率为93.63%,得到的分类结果如下图混淆矩阵所示。该矩阵纵轴为测试集样本的真实信道标签,横轴为经过卷积神经网络识别后得到的信道模型类别,每个方格中的数字为其所占的百分比,为确保分析结果精确,该矩阵中保留小数点后三位。由该矩阵图可以看出,CM2的识别准确率最高,为96.5%,CM4的准确率最低,为90.2%,并且CM1只会被错误的识别为CM2,而不会被识别为CM3或CM4,同样的,CM3只会被错误的识别为CM4,而不会被识别为CM1或CM2。之所以会这样,可以由表2-1得知,CM1和CM2均为室内居住环境,差别为是否为视距状态,因此,CM1和CM2的信道相似度比较高,与CM3或CM4的相似度比较低,故而提取后的特征差别较大。可见,卷积神经网络进行分类识别的结果及误差是与实际应用背景相符合的。
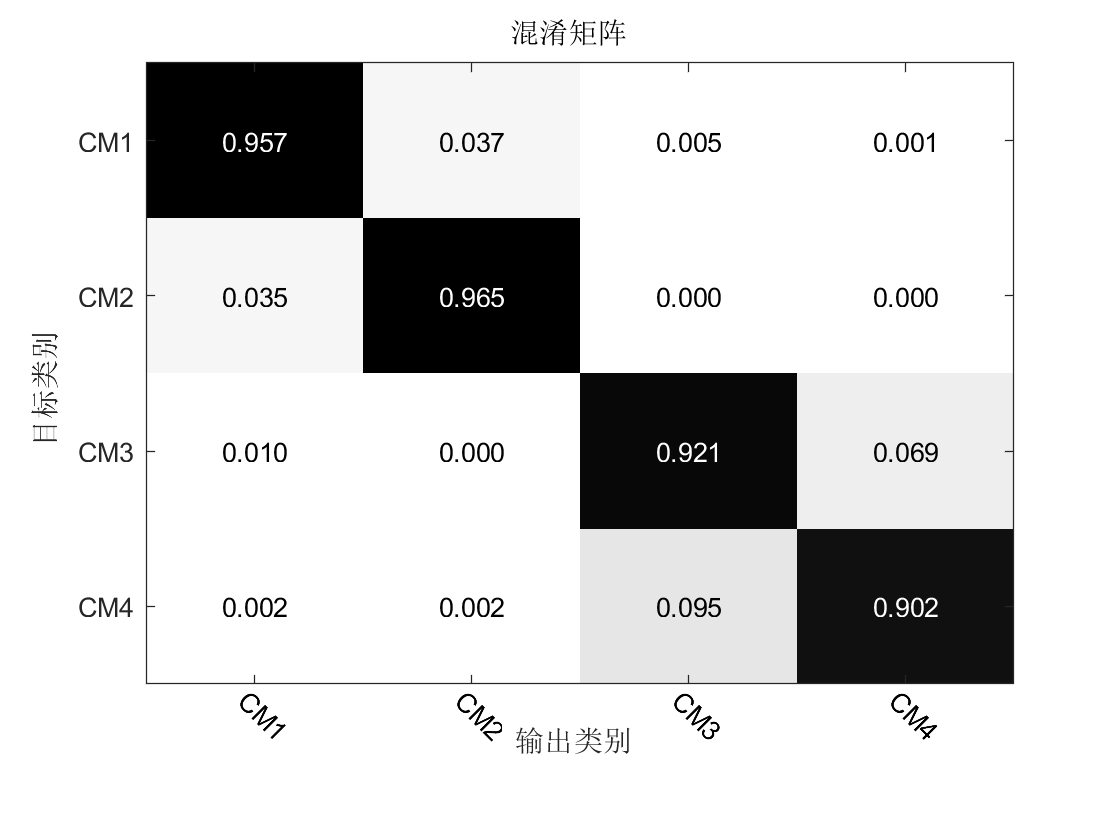
图4-1 各信道测试分类准确率混淆矩阵图
从准确率的角度来看,支持向量机的准确率远不如卷积神经网络网络,平均比卷积神经网络网络低15.46%。从训练时间的角度来看,SVM网络的训练时间较长,约为卷积神经网络的3倍。为了比较算法性能,分别选取支持向量机算法的最佳结构和最佳参数,为突出训练结果的对比性,卷积神经网络算法选取最佳结构,迭代次数仅选为3次,经过多次训练测试取平均值,得到的结果对比如表4-1所示。
表4-1 不同算法实现信道识别结果对比分析
算法 | 每类样本数 | 准确率 /% | 训练时间 次/s |
SVM | 15100 | 77.45 | 62 |
CNN | 15100 | 92.91 | 18.46 |
结论
本文设计了一种用于超宽带室内密集多径信道模型识别的卷积神经网络,该神经网络可以在20秒内实现准确率高达90%以上的信道模型识别,性能远优于传统的支持向量机实现信道模型识别。由此可见,卷积神经网络除了可运用于图像识别外,在无线信号识别方面也有不俗的表现。本文训练数据来源于冲激响应仿真,下一步可使用实测数据作为训练集和测试集,提升该方法的工程实践价值。
参考文献
[1]姚碧圆. 基于图论算法的无线信道特征提取与场景识别研究[D].海南大学,2017:12.
[2]姚凯凌,张玉立,孙有铭.基于时域特性信道指纹的场景识别[J].军事通信技术,2016,37(02):72-76.
[3]王瑞星,刘斌,杜健鹏,李明.基于两种算法的无线信道“指纹”特征识别[J].通信技术,2016,49(10):1271-1279.
[4]Weidong Wang,Junan Yang. A novel compressed sensing ultra‐wideband channel estimation method based on non‐convex optimization[J]. International Journal of Communication Systems,2015,28(3):42-45.
[5]Doaa E, El. Matary. Performance of Polar Codes for OFDM-Based UWB Channel[J]. Journal of Computer and Communications,2018,06(03):14-20.
[6]G. Routraya,P. Kanungo. Genetic Algorithm Based RNN Structure for Rayleigh Fading MIMO Channel Estimation[J]. Procedia Engineering, 2012,30:64-68.