中国船舶集团有限公司第七一○研究所,湖北 宜昌 443003
摘 要:针对磁计量仪器故障模式多样的特点,提出了一种基于改进的贝叶斯优化算法的故障模式聚类分析方法。该算法通过将免疫算法选择优良个体方法与先验信息运算算法这两种方法相结合对贝叶斯优化算法进行改进,既提高了优良种群的多样性同时又避免了信息浪费,从而综合提高了算法的全局性和快速收敛性。在理论上对贝叶斯优化算法在故障模式分析的应用进行了研究。
关键词:磁计量仪器;贝叶斯方法;亲和度;聚类分析
1 引言
贝叶斯优化算法(BOA,Bayesian Optimization Algorithm)使用概率模型来模拟种群中个体的分布情况,是一种基于概率进化的分布估算算法。由于传统的贝叶斯优化算法BOA采用由目标函数值确定的适应度作为优良个体选择依据,对于约束优化问题,采用由罚函数值确定的适应度作为依据。这样会导致优化进行到一定代数之后,所选个体相似度高,个体多样性差,抽样时难以生成更好的新个体,使得算法容易陷入局部最优。另外由于在常规算法中未考虑先验信息,结果又造成了信息浪费不能重复利用数据。
针对上述问题,本文对故障分析中的贝叶斯优化算法进行综合改进:首先是在优秀个体选择上引入了免疫算法中的亲和度和浓度概念,将个体适应度概率和个体浓度概率相结合,形成贝叶斯优化算法选择优良个体的依据。其次是在算法上结合先验信息修正贝叶斯网络,充分利用数据。最后应用改进的算法结合数据最优聚类分析方法,根据聚类分析的相似度和聚类目标函数进行故障判断。
2 贝叶斯优化算法
贝叶斯优化算法是一种基于概率分布的进化算法。BOA使用贝叶斯网络BN来模拟各变量之间相关性,这种相关性反映了模式理论中的模式。贝叶斯网络是一个有向无环图,用它来表示一组变量之间概率关系。在贝叶斯优化算法中,建立贝叶斯网络是算法的核心和关键。如图1所示。
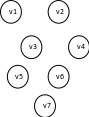
图1 7节点的贝叶斯网络
贝叶斯网络是联合概率分布的图形表示形式。一个贝叶斯网络由两部分组成:结构B和参数θ。结构B是一个有向无环图,其节点表示各个变量,节点之间的有向边表示变量之间的条件依赖关系,两个节点之间若没有有向边,则说明这两个随机变量是相对独立的。
对于有向边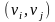 ,
,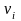 称为
称为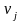 的父节点,而
的父节点,而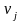 称为
称为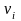 的子节点。参数θ是各变量条件概率分布表的集合,即
的子节点。参数θ是各变量条件概率分布表的集合,即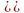 。其中
。其中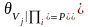 ,表示变量
,表示变量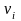 在其父节点集
在其父节点集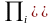 下的条件概率分布。由贝叶斯网络可以将个体的联合条件概率分布为:
下的条件概率分布。由贝叶斯网络可以将个体的联合条件概率分布为:
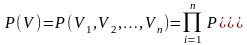 (1)
(1)
贝叶斯网络是用来描述所选择的优秀解的特征和分布,以此来指导新解的生成。为了能够快速构建贝叶斯网络结构,通常采用基于BD打分测度的贪婪算法构建贝叶斯网络。
3 改进的贝叶斯优化算法
通过查阅相关文献资料,发现已有的对贝叶斯优化算法的改进往往有一定的局限性,如只在优良个体选择上进行改进[2]或只在是否结合先验信息运算上进行改进[3],而在优良个体选择上改进后的算法中未考虑结合先验信息,同样在结合先验信息的改进贝叶斯优化算法在个体选择机制上又相对简单,而这两种改进方法恰好能起到长短互补的作用。因此本文提出的改进贝叶斯优化算法的基本思想是:在参考相关资料的基础上将上述两种对贝叶斯优化算法的改进进行优化结合,从而达到最优改进的目的。
首先在优秀个体选择上对贝叶斯优化算法进行改进[2],引入了免疫算法中的亲和度和浓度概念,将个体适应度概率和个体浓度概率相结合,形成贝叶斯优化算法选择优良个体的依据。设有N个个体,每个由S={0,1}中的M个基因组成(一个二进制的字符位串),则第j个基因的信息熵为

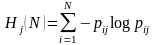 (2)
(2)
式中: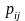 表示S中第i个字符(0或1)在第j个基因位上出现的概率。若在位置j上所有个体的字符都相同,那么
表示S中第i个字符(0或1)在第j个基因位上出现的概率。若在位置j上所有个体的字符都相同,那么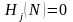 。平均信息熵
。平均信息熵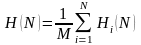 ,它反映了多样性。由此,得到个体u与v之间的亲和度
,它反映了多样性。由此,得到个体u与v之间的亲和度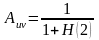 。
。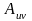 的取值范围为
的取值范围为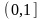 。
。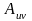 越大表示两个个体基因相似度越高,
越大表示两个个体基因相似度越高,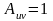 表示两个个体基因完全相同。个体浓度定义为:
表示两个个体基因完全相同。个体浓度定义为: 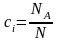 ,
,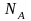 表示与个体
表示与个体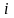 亲和度大于亲和度常数
亲和度大于亲和度常数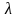 的个体数。
的个体数。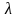 一般取值
一般取值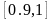 。这样每个个体的评价指标变为:
。这样每个个体的评价指标变为:
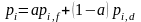 (3)
(3)
式中: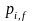 为个体适应度概率,对于最小化问题,目标值/罚函数值越小,
为个体适应度概率,对于最小化问题,目标值/罚函数值越小,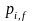 越大,且
越大,且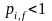 ;
;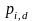 为个体浓度概率,个体浓度越小,
为个体浓度概率,个体浓度越小,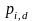 越大,且
越大,且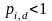 ;
;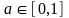 是常数调节因子;若
是常数调节因子;若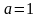 ,则只使用个体适应度概率作为选择依据。以每个个体的
,则只使用个体适应度概率作为选择依据。以每个个体的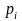 值作为选择依据,使用确定性选择方式,选择种群中
值作为选择依据,使用确定性选择方式,选择种群中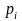 值大的那部分个体组成优良个体集合。这种选择依据能够有效地保持种群的多样性,提高算法的性能。
值大的那部分个体组成优良个体集合。这种选择依据能够有效地保持种群的多样性,提高算法的性能。
另外,通过分析发现,常规算法中没有考虑前一代种群提供的优秀解及构建的贝叶斯网络结构的特点,这样造成了信息浪费,影响构建网络的可靠性。因此可以把前一代网络构建的信息和结构作为后一代构建的先验知识,利用先验知识来修正贝叶斯网络。这样不但可以充分利用数据,而且可以提高所构建网络的可靠性,从而提高算法的收敛速度和全局收敛性。因此本文使用结合先验信息的BD(贝叶斯 dirichletmetric)打分法
[3]。
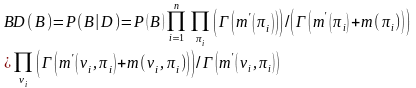 (4)
(4)
其中: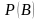 是网络结构B的先验概率;对
是网络结构B的先验概率;对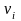 的连乘表示对节点
的连乘表示对节点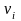 的所有取值进行乘积,对
的所有取值进行乘积,对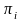 的连乘表示对节点
的连乘表示对节点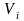 的父节点
的父节点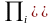 的所有取值的乘积;
的所有取值的乘积;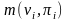 表示数据中
表示数据中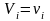 和
和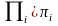 的例子数,
的例子数,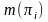 表示数据中
表示数据中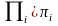 的例子数;
的例子数;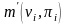 和
和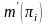 分布表示
分布表示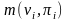 和
和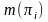 的先验信息,即
的先验信息,即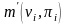 表示先验信息数据中
表示先验信息数据中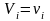 和
和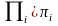 的例子数,其中参数为:
的例子数,其中参数为:
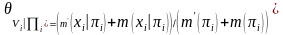 (5)
(5)
如果无先验信息,则令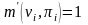 。
。
4 故障模式识别
这里采用文献[3]提出的故障模式识别方法,即根据故障监控状态下系统的测量值进行聚类分析来进行系统的故障诊断。采样数据向量定义如下:
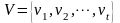
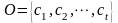 (6)
(6)
其中:vi∈Rd(1≤i≤T)为采样数据向量; ci∈Rd(1≤i≤C)是聚类中心向量。数据x和y之间的方向相似度S(x,y)定义为: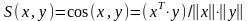
定义如下的聚类目标函数:
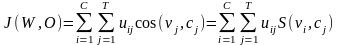 (7)
(7)
其中:W=uij为隶属矩阵。选择如下优化目标函数:
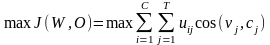 (8)
(8)
其中:s t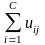 =1,
=1, 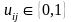 ,
,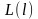 ≤
≤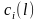 ≤
≤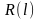 ,1≤
,1≤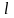 ≤d,1≤i≤C。
≤d,1≤i≤C。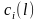 是聚类中心向量的第
是聚类中心向量的第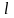 个元素;
个元素;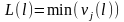 ,
,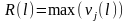 ,1≤j≤T。迭代终止条件为:
,1≤j≤T。迭代终止条件为: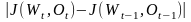 ≤
≤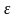 ,
,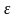 取任意小的正数。对采样数据V的聚类就是在上述约束条件下优化
取任意小的正数。对采样数据V的聚类就是在上述约束条件下优化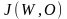 。那么故障模式分类问题就转换为求解带约束的最优化聚类问题。
。那么故障模式分类问题就转换为求解带约束的最优化聚类问题。
5 故障模式分类算法及运算过程
本文通过将上述两种对贝叶斯优化算法的改进融合起来形成一种新的改进后的贝叶斯优化算法,这种算法和常规的贝叶斯优化算法相比,既在优良个体选择上引入了免疫算法的亲和度和浓度的概念始终保持选择优良个体,又结合了先验信息提高了算法的快速收敛性。根据上文的聚类分析方法,以下就是本文提出的基于改进的贝叶斯优化算法的故障模式分类算法及运算过程:
根据系统实测数据,随机初始化种群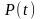 ,设置种群规模
,设置种群规模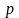 ,参数
,参数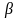 ,参数
,参数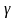 ,常数调节因子
,常数调节因子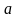 ,亲和度常数
,亲和度常数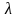 ,令进化代数
,令进化代数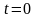 。
。
将个体适应度概率和个体浓度概率一起(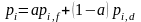 )作为评价依据。从
)作为评价依据。从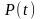 中选择部分优秀个体(
中选择部分优秀个体(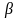 个),组成集合
个),组成集合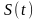 。
。
设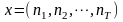 为算法的一个解,那么把它转换为隶属矩阵
为算法的一个解,那么把它转换为隶属矩阵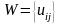 ,并且更新聚类中心向量:
,并且更新聚类中心向量: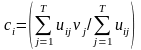 ;由式(7)计算聚类目标函数
;由式(7)计算聚类目标函数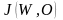 ,作为适应度函数。
,作为适应度函数。
由集合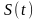 ,利用贪婪算法和结合先验知识的BD打分构建贝叶斯网络概率模型建立
,利用贪婪算法和结合先验知识的BD打分构建贝叶斯网络概率模型建立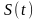 的概率分布。
的概率分布。
依据概率分布,即对构建出来的网络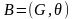 进行抽样,生成
进行抽样,生成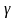 个新个体,组成集合
个新个体,组成集合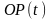 。
。
将个体适应度概率和个体浓度概率一起(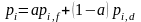 )作为评价依据。从
)作为评价依据。从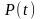 和
和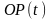 中选择
中选择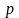 个优良个体,形成新的种群
个优良个体,形成新的种群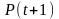 ,令
,令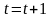 。
。
判断收敛条件是否满足,若满足,停止计算。否则转至2)。种群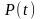 为所求解。
为所求解。
根据所得的聚类中心和相似度函数值,对测试数据进行测试,以判断所采集的数据属于哪一类,即进行故障模式分类。
由以上运算过程可知,本文对贝叶斯优化算法的改进主要体现在:在算法步骤2)和6)中引入了个体适应度概率和个体浓度概率作为选择优秀个体的评价依据,这种选择依据能够有效地保持种群的多样性,提高算法的性能。同时在构建贝叶斯网络的步骤4)中的BD打分运算时结合先验信息,充分利用数据,提高了构建网络的可靠性。
6 结束语
本文对故障分析中的贝叶斯优化算法进行了综合优化改进。算法既引入了免疫算法中的亲和度和浓度概念提高了选择种群分布的多样性,又具有结合先验信息运算的快速收敛性,最后结合聚类分析方法完成了故障模式分类。本文的方法对磁计量仪器的故障分析有一定的借鉴作用。
参考文献
[1] 宋蕾. 优化贝叶斯的数据融合算法[J].电子技术与软件工程,2019,6
[2] 曾国斌,冉兆春. 基于贝叶斯算法的神经网络优化方法研究[J].数码世界.2017,12
[3] 梁瑞鑫,张长水,郭国营,等. 一种混沌贝叶斯优化算法[J].计算机工程与应用.2004,36
[4] 周东华,叶银忠.现代故障诊断与容错控制[M]. 清华大学出版社: 2008.
[5] 钟小平,李为吉,等. 改进的贝叶斯优化算法及应用[J]. 机械科学与技术,2006,4.
[6] 刘小雄,武燕,等. 一种故障诊断的贝叶斯优化算法研究[J]. 计算机应用研究. 2009,1