陕西省合阳县第二高级中学 715300
【摘要】:不等式是贯穿高中数学的一根主线,高考对不等式的考察注重与函数相结合.运用函数思想、分类讨论思想、数形结合等思想对问题予以解决,此类问题往往多出现在解答题中,而在某一小问中又多于含参不等式恒成立问题中求参数取值范围形式为主,对此本文就此类恒成立问题中出现的常见方法做出了简单地归纳总结.
【关键词】:含参不等式 恒成立 构造函数法
1.二次函数法
例1.已知函数![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解:要使![]() 在
在![]() 上恒成立
上恒成立
由一元二次函数的性质可知:
![]() 或
或![]()
解得![]()
∴满足题意的实数![]() 的取值范围为
的取值范围为![]()
评注:与二次函数有关恒成立问题通常采用数形结合的方法求解,
一元二次不等式![]() 在
在![]() 上恒成立
上恒成立![]() ,
,
一元二次不等式![]() 在
在![]() 上恒成立
上恒成立![]() ,
,
不等式在给定区间上恒成立则
![]()
![]()
2.分离变量构造函数法
例2.已知函数![]() .
.
求(1)![]() 的最小值;
的最小值;
(2)若对所有![]() ,
,![]() 恒成立,实数
恒成立,实数![]() 的取值范围.
的取值范围.
解:(1)由题意![]()
令![]() 得
得![]()
列表如下:
| | | |
| - | 0 | + |
| | 极小值 | |
∴由上表得![]()
(2)![]() 在
在![]() 上恒成立
上恒成立
即![]() 在
在![]() 上恒成立
上恒成立
∴![]()
令![]()
![]()
列表如下:
| | | |
| - | 0 | + |
| | 极小值 | |
由表得![]()
∴实数![]() 的取值范围为
的取值范围为![]()
评注:由不等式恒成立求解参数取值范围的问题也常采用分离参数求最值的方法予以解决,即要使![]() 恒成立,只需
恒成立,只需![]() 即可;要使
即可;要使
![]() 恒成立,只需
恒成立,只需![]() 即可,但应参数便于分离,并且构造的函数便于求最值.
即可,但应参数便于分离,并且构造的函数便于求最值.
3.直接构造函数法
例3.(渭南市16级高三市一模)已知函数![]() ,设
,设
![]() ,当
,当![]() 时,
时,![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
解:由题意得对任意的![]() ,
,![]() 恒成立
恒成立
设![]()
∴![]() 在
在![]() 上恒成立
上恒成立
即![]()
![]()
当![]() 时,
时,![]()
![]() 时,
时,![]() ,
,
∴![]() 在
在![]() 单调递减,故
单调递减,故![]() 满足题意
满足题意
当![]() 时,
时,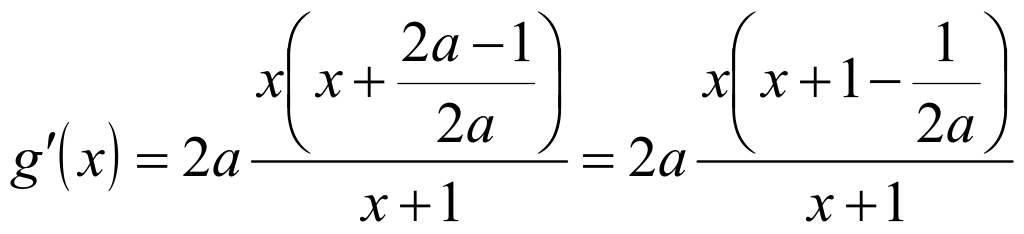
当![]() 时,
时,![]()
![]()
∴![]() 在
在![]() 单调递减,故
单调递减,故![]() 也满足题意
也满足题意
当![]() 时,若
时,若![]() ,即
,即![]() ,
,![]() 在
在![]() 上递减,在
上递减,在
![]() 上递增,故
上递增,故![]() 无最大值,不满足题意
无最大值,不满足题意
若![]() ,即
,即![]() ,
,![]() 在
在![]() 上递增,
上递增,![]() 无最大值,故也不满足
无最大值,故也不满足
题意
综上所述:实数![]() 的取值范围为
的取值范围为![]()
评注:在解决某些含参不等式恒成立问题时,若分离参数会遇到讨论的麻烦或参数容易分离但构造的函数的最值不易求出,此时也可直接构造函数,结合条件求其最值进而确定参数的取值范围.
4.变换主元法
例4.已知函数![]() ,若
,若![]() .
.
(1)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的范围;
的范围;
(2)当![]() 时,不等式
时,不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
解:(1)不等式变形为![]()
令函数![]()
![]()
要使![]() ,则由一次函数性质可知:
,则由一次函数性质可知:![]()
解得![]() 的取值范围为:
的取值范围为:![]()
(2)∵![]()
∴![]()
∴不等式可化为![]()
又∵![]()
∴![]()
即![]() 的取值范围为
的取值范围为![]()
评注:解决含参不等式恒成立问题时,若能适时的把主元变量和参数变量进行“换位”思考,往往会使问题简化.
解决不等式恒成立问题时,通常要借助于函数思想构造出适当的函数,利用函数的性质转化为求函数的最值来求解参数的取值范围.
参考文献:
[1] 黄艳珍.有关不等式恒成立问题的探析[J].考试(教研版):2008(01).
[2] 顾冬梅.不等式恒成立问题的常用解法[J].新课程学习(基础教
育):2010(01).
[3] 朱峰.不等式恒成立问题中参数范围的求法[J].中学数学研究:2010(02).