丽水中学 323000
前苏联著名学者AK加斯切夫曾说过,数学,常被称为“关于无限的科学”,没有无限概念是不可能走进数学的.
无穷与极限的思想是中学数学中的重要思想,它从数量上描述了变量在运动过程中的变化趋势,用无限与逼近的方式从有限中认识无限,从近似中认识精确,从量变中认识质变.虽然极限知识在现行教材中已经淡化,但无穷与极限的思想仍贯穿高中数学的各个部分.在解决问题时有不可忽视的作用.本文就结合高中教材,略谈无限思想在教学中的渗透.
一.通过“几类不同增长的函数模型”教学,培养学生把握函数的整体形态.
在人教版必修一《几类不同增长的函数模型》这节教学时,常见的做法是通过计算机结合图象比较一次函数,幂函数,指数函数,对数函数随着自变量增大时增长速度的不同.学生对此的理解可能只停留在定性直观感知上,不够深刻。若如我们循序渐进配上例题,往往能较好的培养学生整体把握函数形态.
例1.(2009江西理12)已知函数![]() ,若对一切实数x,f(x)与g(x)的值至少有一个为正,则m的取值范围为______________.
,若对一切实数x,f(x)与g(x)的值至少有一个为正,则m的取值范围为______________.
解析:当m=0时,不满足,当m≠0时,x→![]() ∞,g(x)为一正一负,而f(x)确同号,故只能同正,从而m>0.即只需f(x)在区间
∞,g(x)为一正一负,而f(x)确同号,故只能同正,从而m>0.即只需f(x)在区间![]() 恒正即可.对称轴为
恒正即可.对称轴为![]() ,所以
,所以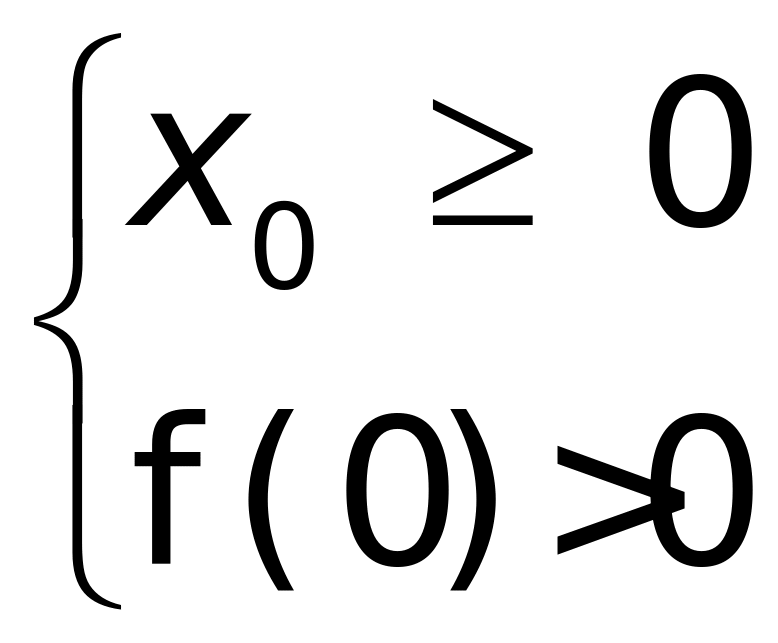 或者
或者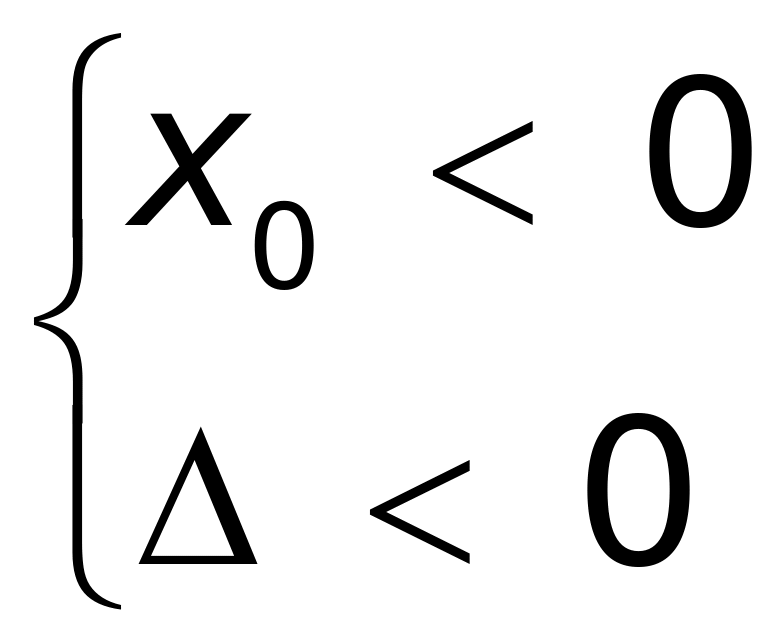 .解得0
.解得0
例2.(2013新课标理21)设函数![]() ,若当x≥-2时,
,若当x≥-2时,
f(x)≤kg(x),求k的取值范围.
解析: f(x)≤kg(x) ![]() .
.
![]()
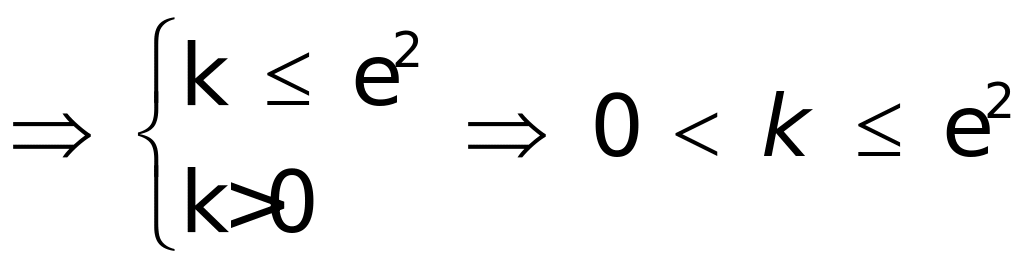
![]() ,x=-lnk≥-2.于是h(x)在
,x=-lnk≥-2.于是h(x)在![]() 上递减,在(-lnk,+ ∞)上递增.
上递减,在(-lnk,+ ∞)上递增. ![]() ,解得1≤k≤e2
,解得1≤k≤e2
二.通过“为什么![]() 是双曲线
是双曲线![]() 的渐进线”教学,培养学生在无限变化的过程看图形的变化规律.
的渐进线”教学,培养学生在无限变化的过程看图形的变化规律.
人教版选修2-1 P62页的“探究与发现”部分,介绍了为什么![]() 是双曲线
是双曲线![]() 的渐进线.用极限知识生动解释了渐进的含义. 双曲线的渐近线是双曲线退化的极端情形.材料后面凸显的是用动态的观点看曲线图形的变化规律.通过以下例子让学生养成在无限变化的过程看图形变化规律.
的渐进线.用极限知识生动解释了渐进的含义. 双曲线的渐近线是双曲线退化的极端情形.材料后面凸显的是用动态的观点看曲线图形的变化规律.通过以下例子让学生养成在无限变化的过程看图形变化规律.
例3. (2012浙江高考理8)如图1,F1,F2分别是双曲线C:![]() (a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则C的离心率是(B )
(a,b>0)的左、右焦点,B是虚轴的端点,直线F1B与C的两条渐近线分别交于P,Q两点,线段PQ的垂直平分线与x轴交于点M,若|MF2|=|F1F2|,则C的离心率是(B )
A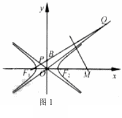
![]() B
B ![]()
C ![]() D
D ![]()
解析:设PQ中点N(x0,y.0),M(3c,0),
直线PQ的斜率![]() ,从而直线MN的斜率
,从而直线MN的斜率![]()
N是直线PQ与两渐近线![]() 的交点中点,利用点差法,类似双曲线有
的交点中点,利用点差法,类似双曲线有![]() .从而有方程
.从而有方程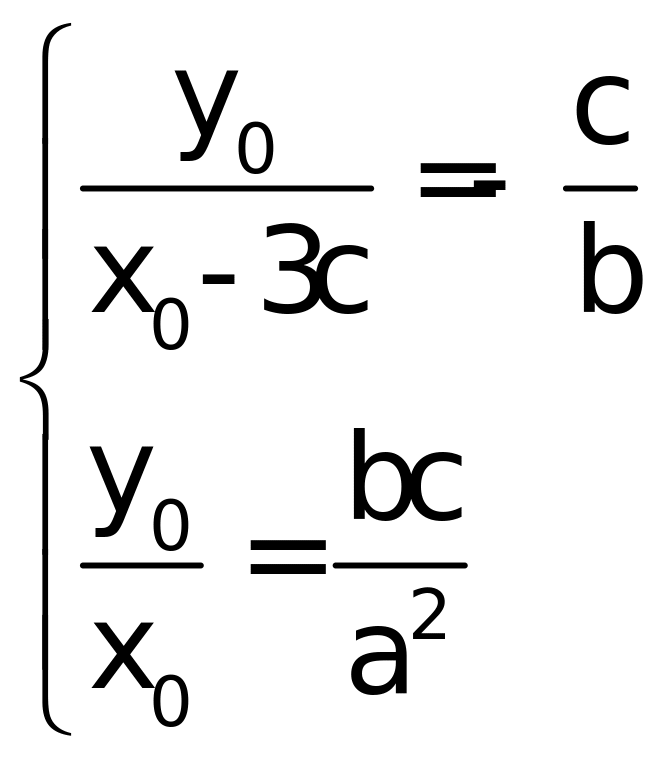 ,解得
,解得![]() .
.
又点N、B、F1三点共线.有![]() ,得3a2=2c2,
,得3a2=2c2, ![]() .
.
例4. (2014浙江高考理16)设直线![]() 与双曲线
与双曲线![]() 的两条渐近线分别交于点A、B,若点
的两条渐近线分别交于点A、B,若点![]() 满足
满足![]() ,则该双曲线的离心率是______________.
,则该双曲线的离心率是______________.
解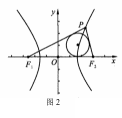 析:方法同例3.求得
析:方法同例3.求得![]()
例5.如图2 F1、F2分别是双曲线C:![]() (a,b>0)
(a,b>0)
的左、右焦点,P为右支上的一点,则△PF1F2的内切圆的圆心
横坐标为
A a B b C c D a+b-c
解析:当P延双曲线向右顶点无限接近时,内切圆逐渐变小
直至一个点,此点为右顶点.故选A
三.通过“柱体、锥体、台体体积公式”的教学,培养学生通过动态的看待空间几何体,几何量,养成猜想、验证、合情推理的能力.培养学生的创新精神.
人教版必修2 P26页,在得出柱、锥、台的体积公式后,安排了一个“思考”.目的是引导学生思考柱体、锥体、台之间的关系,培养学生地看待动态几何体.几何体作为直观、形象的数学模型,学生在用观察、操作、猜想、设计、作图等手段探索研究的过程中获得视觉上的愉悦,增强好奇心,激发出潜在创造力,形成创新意识.以下例子就有很好的作用.
例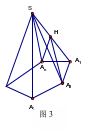 6. 正
6. 正![]() 棱锥中,相邻两侧面所成的二面角的取值范围是( )
棱锥中,相邻两侧面所成的二面角的取值范围是( )
A(![]() ) B(
) B(![]() )
)
C(![]() ) D(
) D(![]() )
)
解析:如图3 当正棱锥的顶角无限接近底面时,两侧面所成的二面角无限接近![]() .当正棱锥的高无限增大时,两侧面所成的二面角无限接近正
.当正棱锥的高无限增大时,两侧面所成的二面角无限接近正![]() 多边形的一个内角,即为
多边形的一个内角,即为![]() ,因此,所求二面角的范围应为(
,因此,所求二面角的范围应为(![]() )
)
例7.(2005全国卷三理8)如图4设三棱柱ABC—A1B1C1的体积为V,P、Q分别是侧棱AA1,CC1上的点且满足PA=QC1,则B—APQC的体积为( )
A ![]() B
B![]() C
C ![]() D
D ![]()
解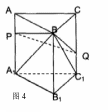
 析:本题体积为定值,可考虑P与A重合,Q与C1重合时,三棱锥B—ACC1的体积为
析:本题体积为定值,可考虑P与A重合,Q与C1重合时,三棱锥B—ACC1的体积为![]() .故选A
.故选A
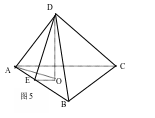
例8.(2017高考模拟卷题9) 如图5,已知三棱锥D-ABC,记二面角C-AB-D的平面角是θ,直线DA与平面ABC所成的角是θ
1,直线DA与BC所成的角是θ2,则
A.θ≥θ1 B.θ≤θ1 C.θ≥θ2 D.θ≤θ2
解析:根据最小角定理,线面角是这条斜线与这个平面内的任一直线所成角中的最小角, 所以有θ1≤θ2,而二面角是所有线面角中最大的.因而有θ≥θ1 .
例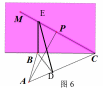 9.(2014浙江卷理17)如图6,某人在垂直于水平地面
9.(2014浙江卷理17)如图6,某人在垂直于水平地面![]() 的墙面前的点
的墙面前的点![]() 处进行射击训练.已知点
处进行射击训练.已知点![]() 到墙面的距离为
到墙面的距离为![]() ,某目标点
,某目标点![]() 沿墙面的射击线
沿墙面的射击线![]() 移动,此人为了准确瞄准目标点
移动,此人为了准确瞄准目标点![]() ,需计算由点
,需计算由点![]() 观察点
观察点![]() 的仰角
的仰角![]() 的大小.若
的大小.若![]() 则
则![]() 的最大值 .(仰角
的最大值 .(仰角![]() 为直线AP与平面ABC所成角)
为直线AP与平面ABC所成角)
解析:AP是平面AMC内的动直线,因此当直线AP与平面ABC
所成角与二面角M—AC—B相等时线面角最大.所以本题只需过点B,
分别在墙面和地面内作BC和AC的垂线,交MC,AC于E,D两点.则
∠EDB为二面角的平面角.可求得BC=20,BE=![]() ,BD=12.
,BD=12.
故tan![]() 的最大值为
的最大值为![]() .
.
极限思想在很多的问题的思考中,也许算不上是一种严密的方法,但它至少可作为一种猜想或验证结论的工具.在越来越重视合情推理的今日数学教学中,培养学生用极限思想去分析思考问题是必要的.
参考文献:1.[美]M.克莱因《古今数学思想》 上海科学技术出版社.
2. 顾泠沅.《作为教育任务的数学思想与方法》 上海教育出版社.
5