青岛农业大学 理学与信息科学学院
摘要:本文研究了微积分的思想和方法在托里拆利小号问题中的应用,并对相应结论进行了讨论和延伸,为高等数学的教学方式和其他领域的研究提供启发。
研究背景
微积分蕴含着极其深刻丰富的哲学原理与数学思想,微积分学的创立,被恩格斯誉为十七世纪数学领域最伟大的三大发现之一。恩格斯曾这样评价过微积分:“在一切理论成就中,未必再有什么像微积分的发现那样般的人类精神的最高胜利了。”微积分既有重要的理论意义,还在很多实际问题中有着广泛的应用价值[1,2,3]。该理论既为我们通过有限的数量关系来认识无穷提供了有力的思想和方案,也为我们分析和解决自然科学、工程技术、社会科学中出现的诸多实际问题给出了解决方法。
在微积分的教学中,定积分是其中非常重要的一部分内容,它蕴含着重要的微元法、极限、探讨无穷的思想、方法与哲理。我们在定积分的教学中,既要突出教学大纲中的重点、难点,使学生掌握定积分的定义与各类计算方法,同时还要激发学生的学习热情,以避免学生在面对大量的题目时会丧失学习兴趣和动力,在茫茫的数学题海中消耗学习激情和求知热情。在课堂教学中创设情境,适当地提出好问题,是一种值得探索的教育模式。通过引入少而精的引人入胜的有趣问题实例,促使学生深度思考、解放思想,充分发挥想象力和创造力,勇于用创新思维去思考问题、分析问题、解决问题、总结问题,这样才能使学生在快乐中学习,更有效地掌握好相关内容[4,5]。
基于这方面考虑,我们在教学过程中尝试把托里拆利小号问题[5]和定积分的思想及应用结合起来,使学生切身体验到思考、应用定积分过程中的乐趣,进而激发起学生热切的求知欲和浓厚的学习兴趣,化被动学习为主动学习,培养学生运用数学思维来思考问题、分析问题的逻辑思维习惯,提高学生用数学知识来构建实际问题的数学模型、用数学的定量方法来解决问题的素质和能力。
托里拆利小号问题与微积分的应用
托里拆利是17世纪意大利著名的物理学家、数学家,是伽利略的学生和助手,接替了伽利略的物理学和数学教授职位,并被任命为当时意大利的宫廷首席数学家。在科学史上,托里拆利以发明水银气压计而闻名于世,而且他还有非常高的数学造诣和贡献。
在数学方面,托里拆利曾提出过一个非常有趣的问题,名为“托里拆利小号问题”:考虑XOY直角坐标平面上的双曲线 ![]() (当
(当![]() 时的部分),将该曲线绕x轴旋转一周得到的立体记作Ω,注意到该立体形状极其像是一个小号,因此被称为托里拆利小号。我们来探讨托里拆利小号Ω的体积和表面积的计算,其解答过程涵盖了高等数学里的定积分(无穷限的反常积分情形)、空间立体几何、二重积分等多个方面的内容和方法,通过该题目的练习,可以考察学生对积分学知识的理解程度和综合应用能力。另一方面,从该题目的解答结果中还可以发现一些非常有趣的现象,引发我们的深度思考,激发学生进一步的求知欲和学习热情。
时的部分),将该曲线绕x轴旋转一周得到的立体记作Ω,注意到该立体形状极其像是一个小号,因此被称为托里拆利小号。我们来探讨托里拆利小号Ω的体积和表面积的计算,其解答过程涵盖了高等数学里的定积分(无穷限的反常积分情形)、空间立体几何、二重积分等多个方面的内容和方法,通过该题目的练习,可以考察学生对积分学知识的理解程度和综合应用能力。另一方面,从该题目的解答结果中还可以发现一些非常有趣的现象,引发我们的深度思考,激发学生进一步的求知欲和学习热情。
定积分方法
注意到Ω是平面曲线绕坐标轴旋转一周生成的旋转体,计算旋转体的体积与表面积是定积分的两个重要应用。根据绕x轴的旋转体体积与表面积的定积分计算公式,我们可以得到
Ω的体积V =![]() , (1)
, (1)
Ω的表面积A =![]() , (2)
, (2)
其中,(1)的结果是由幂函数的基本积分公式与无穷限反常积分的计算公式得到的;
(2)则通常可以由两种方法来计算:第一种方法是结合正切函数换元x = tan t与无穷限反常积分的计算公式求得,第二种方法是通过无穷限反常积分的比较审敛法可证明该反常积分的发散性。
二重积分方法
首先,利用空间解析几何给出的旋转曲面方程的表示方法,我们可以得到托里拆利小号正是如下空间直角坐标点集表示的立体:
![]() ,
,
其中![]() 是空间立体Ω在YOZ直角坐标平面上的投影区域。因此,根据空间立体的体积与曲面面积的二重积分计算公式可得
是空间立体Ω在YOZ直角坐标平面上的投影区域。因此,根据空间立体的体积与曲面面积的二重积分计算公式可得
![]() 的体积V =
的体积V =![]() , (3)
, (3)
![]() 的表面积A =
的表面积A =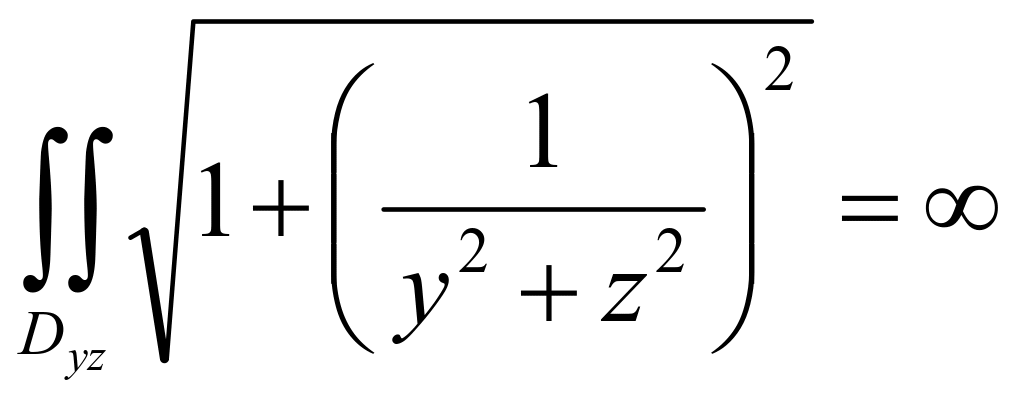 。 (4)
。 (4)
讨论与启发
托里拆利小号问题涉及到的知识点
托里拆利小号问题的计算过程综合运用了微积分的以下多个方面知识:(1) 旋转体体积与表面积的计算方法;(2) 无穷限情形的反常积分的计算与审敛法;(3) 不定积分的求法:比如三角换元法;(4) 旋转曲面方程与空间立体的点集表示;(4) 空间立体体积与曲面面积的二重积分计算公式;(5) 二重积分的极坐标变换计算方法。
该题目涵盖了空间立体几何、定积分与二重积分的多方面内容,可以帮助学生更深刻地
理解和熟练运用各种积分方法,还能训练学生养成逻辑推理分析、定量思维习惯以及理论联系实际的数学计算与解决问题的能力,进而达到素质教育的目的。
结果讨论
以上计算结果揭示了一个非常有趣的现象:托里拆利小号是一个有限体积、但表面积无穷大的立体,这违背了我们的直观认识!即便是有限长度的托里拆利小号,比如开口直径是d,长度是L的托里拆利小号,其中L远大于d,也会出现体积小于![]() 、而表面积却特别大的现象,这也与我们的直观相违背。原因在于,当我们用油漆去刷这样的托里拆利小号时,刷小号表面所消耗的油漆量(由小号的表面积A 决定),会远远多于小号内部所能容纳的油漆量(由小号的体积V所决定),这不符合我们的直观认识。
、而表面积却特别大的现象,这也与我们的直观相违背。原因在于,当我们用油漆去刷这样的托里拆利小号时,刷小号表面所消耗的油漆量(由小号的表面积A 决定),会远远多于小号内部所能容纳的油漆量(由小号的体积V所决定),这不符合我们的直观认识。
这给我们如何认识体积、面积提出了问题,这能激发学生的深度思考和热烈讨论,使得数学课堂生动有趣。体积和面积这两个基本、初等的概念里蕴含着非常丰富深刻的思想,比如维度、量纲等理论,引人深思。
问题延伸
托里拆利小号问题给我们提供了进一步的遐想和深度思考的空间,是否还存在其它形状的立体也具有这种类似的有趣特性:立体的容积有限,而表面积却可以任意大?
这类问题有着以下实际应用前景:如何在有限体积的空间内,构造表面积可以足够大的封闭曲面。比如人体的大脑、肠道都是这种局限在有限体积的空间内,却具有比较大表面积的器官组织。因此,托里拆利小号问题产生的思想和方法在生命科学、工程技术的研究中也将会有很多用武之地,亟待我们去挖掘和探索。
参考文献
同济大学数学系. 高等数学(第七版上册)[M]. 北京: 高等教育出版社, 2014: 270-293.
陈秀荣, 陈建毅, 修宗湖. 恒温洗浴热水添加策略研究[J]. 数学建模及其应用, 2016, (2): 25-36.
李秀珍. 微积分及其应用(上册)[M]. 北京: 机械工业出版社, 2014: 199-214.
崔文善, 王殿坤, 吴自库. 加强“高等数学”优质课程[J]. 山西财经大学学报, 2009, (S2): 271-272.
王锐, 姜艺佼. “互联网+”技术对提升大学课堂教学成效的推动作用[J]. 文教资料, 2018, (11): 194-195.
M. Carroll, S. Dougherty, D. Perkins. Infinitesimals and a Tale of Seventeenth-Century Mathematics[J]. Math. Mag. 2013 (86): 239-254.
课题名称:青岛农业大学思想政治教育研究课题