贵州省遵义市余庆县平场小学 贵州 遵义 564407
摘要:小学数学学科一直是小学教学之中极为重要的一个学科,其中分数应用题教学更是重点,而在分数应用题的学习中,其难度也会逐渐增加,这对于学生而言是一个极大的挑战,只有加强学生的解题技巧,就可以帮助学生轻松解决复杂分数应用题,而这也是众多小学数学教育者面临的问题。
关键词;复杂分数应用题;小学数学;解题方法
数学是一门逻辑体系严密的学科,严谨是数学科学理论的基本特征之一。小学分数应用问题教学是小学数学教学的核心内容,数字之间的关系是抽象而复杂的,是教学中的一个难点。在小学数学教学中,分数应用题是学生学习过程中的一个难点。而在实际的教学之中也发现,掌握复杂分数应用题的解题技巧,可以降低题目难度,确保学生解题准确性,增强学生数学学习效果[1]。本次旨在对小学数学中复杂分数应用题的答题方式进行教学,帮助学生掌握简单且有效的解题技巧。详细研究内容见下文:
理论知识教学
分数意义
所谓“分数”,就是将单位“1”平均分成几份,代表这样一份或几份的数量,称为分数。这个概念要注意:1.单位“1”,把所有需要平均分的东西作为一个整体,用单位“1”表示,也被称为整体“1”。整体“1”被分为三种情况:一个对象,一个计量单位或由几个物体组成的整体。2. 平均分数,是以平均分为基础的,也就是说,分的每份数都是相等的。因此,有必要加强分数意义的教学,使学生能彻底理解分数的意义。在教学中,应集中训练学生解释分数意义概念中的关键点。
数乘分数意义
学好分数乘法是非常重要的,分数乘整数的意义与整数乘法的意义相同,就是求几个相同加数的和的简便运算。一个数与分数相乘,可以看作是求这个数的几分之几是多少。分数乘整数时,用分数的分子和整数相乘的积做分子,分母不变。能约分的要先约分;分数乘分数,用分子相乘的积做分子,分母相乘的积做分母,能约分的先约分[2]。
分数除法意义
与整数除法相同,分数除法是“通过知道一个因数和其中一个因数的小数求出一个因数的运算”。乘法和除法彼此相反。在教学中,教师应根据分数乘法的含义加深学生对分数除法的理解,使学生清楚地了解分数乘法与除法的区别和联系。
具体解题方式教学
1、基础技能训练
在教学中,找出应用题中的量是分析量关系的前提,这对于学习困难的学生尤为重要。指导学生用“圈”、“画”等方法找出问题中的数量,并阐明问题中所包含的数量;该折线图在理解考分应用题时具有直观直观的特点,有助于学生进一步理解数量关系。有利于提高分析能力的方法。要正确解决分数乘法和除法的应用问题,必须学会画线图;寻找等价关系的训练必须与学生的实际情况密切相关,学生必须首先阅读问题,明确它是系综合关系还是比较关系。
2、单位“1”两个基本公式解题方式
数学学习讲究从易到难,循序渐进。学习复杂分数应用题也是如此,始终离不开单位“1”的问题——判断单位“1”是否已知,最后决定用乘或除法解题的策略。若单位“l”的数已知时,用乘法解题,即单位“1”的量× (所求量占单位“1”的对应分率)=所求量;若单位“1”的数未知(要求单位“1”)时,则用除法解题,即已知量÷
(所求量占单位“1”的对应分率)=所求量;若单位“1”的数未知(要求单位“1”)时,则用除法解题,即已知量÷ (已知量占单位“1”的对应分率)=单位“1”的量。掌握上述两个公式,遵守上述原则,将为解决复杂分数应用问题奠定基础。只有当主体稍微复杂一点时,相应的数量比例不是一目了然,而是隐含在主体的数量关系中,需要进一步分析才能得出[3]。
(已知量占单位“1”的对应分率)=单位“1”的量。掌握上述两个公式,遵守上述原则,将为解决复杂分数应用问题奠定基础。只有当主体稍微复杂一点时,相应的数量比例不是一目了然,而是隐含在主体的数量关系中,需要进一步分析才能得出[3]。
例题:书店卖出一批书,第一天卖出总数的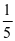 ,第二天卖出去剩下的
,第二天卖出去剩下的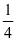 ,第三天卖完剩下的60本,那么这批书共有多少本呢?
,第三天卖完剩下的60本,那么这批书共有多少本呢?
思路与解题方式:我们知道,单位“1”不统一的分率是不能直接相加减的,需要转化单位“1”,让它们统一起来。题中两个分率单位“1”不同,以总数为单位“1”,把“第二天卖出余下的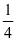 转化为总数的(1一
转化为总数的(1一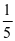 )×
)×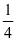 =
=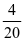 =
=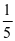 ,最后找到60的对应分率为(1一
,最后找到60的对应分率为(1一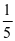 一
一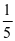 ),列式为80÷(1一
),列式为80÷(1一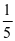 一
一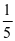 )=100(本)。
)=100(本)。
例题:学校开展课外兴趣小组活动,文艺组与体育组的人数比是4:3,后来文艺组又增加了4人,这时体育组人数是文艺组人数的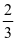 ,文艺组现在有多少人?
,文艺组现在有多少人?
思路与解题方式:对于单位“1”的量不统一的分数应用题,题目中的一些量也在不断地发生变化,但无论其他量怎么变,其中一个量是固定不变的。我们从中找到这个不变量,以它为单位“1”,便能快速找到解题方法。此题的体育组人数始终都不变,我们就以它为单位“1”。变化前文艺组占体育组的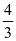 ,变化后,文艺组占体育组的
,变化后,文艺组占体育组的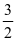 ,这样就找到4人的对应分率是(
,这样就找到4人的对应分率是(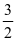 一
一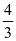 ),列式为4÷(
),列式为4÷(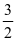 一
一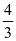 )=24(人),文艺组现有24×
)=24(人),文艺组现有24×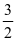 =36(人)。
=36(人)。
结论
综上所述,小学数学教学过程中,对于复杂分数应用题的教学难度较大,为了帮助学生更好的解决此类题型,需要教师对复杂分数应用题的解题方法进行归纳总结,寻找到更为简便有效的解题方法对学生进行指导,并在教学过程中,对学生的学习兴趣进行激发,促使学生积极主动探索数学知识内容,从而有效提高小学数学学习效果和质量。
参考文献
[1]王芳.小学数学稍复杂分数应用题的教学策略[J].关爱明天,2016,(4):248-249.
[2]陈清平.如何进行有效的探究性学习 ——以"稍复杂分数应用题"的教学为例[J].西部素质教育,2017,3(1):235.
[3]柳军民.巧抓不变量解分数应用题——稍复杂分数应用题解题方法初探[J].新课程·下旬,2017,(11):101.