广东省 深圳市龙岗区横岗高级中学,广东 深圳 518115
摘要:本文针对学生不易掌握导数含参数问题中参数该如何分类的问题,通过对几个典型问题的探究,结合流程图来对参数的分类方法和含参数问题的求解步骤来进行总结,形成解决此类问题的模式化解题方法。用流程图来体现参数的分类方法,直观明了,易理解,将解题思想流程化,易操作。
关键词:流程图 导数 含参数问题 参数的分类
一、问题的提出
在高考压轴题的导数综合问题里,我们几乎一定会遇到含参数问题。在这些问题中,有些可以通过分离参数来求解,但有些必须通过对参数进行讨论来求解,而如何对参数进行分类讨论,对学生来说却是一个很难把握的问题。
对此,我们有必要进行一个系统化的归纳和总结。为了学生便于掌握,我想结合流程图来对参数的分类方法和含参数问题的求解步骤来做个总结,形成解决此类问题的模式化解题方法,推翻横在学生面前的大山。
二、问题的剖析
分析和整理近年来的大量高考题,我发现导数含参数问题的表现形式虽然多种多样,包括考察函数单调性问题、不等式恒成立问题、存在性问题、零点个数问题等。归根结底,主要考察函数的零点、函数的单调性、函数的极值、函数的最值等相关知识,而运用导函数来研究原函数图像的特征,是解决一切问题的关键。所以,我们在解决问题时要牢牢把握一个关键--导函数值的正负决定原函数的增减性。要研究导函数值的正负,就要关注导函数的零点,因为除驻点外的导函数的零点是原函数单调区间的分界点。大部分时候,我们要讨论的就是导函数的零点是否存在,或导函数各零点之间的大小关系等。
为了逐步深化对问题的认识,也为了使考试利益最大化,对参数进行分类讨论的基本原则是:先易后难,先简单后复杂。也就是先讨论原函数为单调函数的情况,再讨论原函数不单调的情况;分别对应于导函数恒大于等于0(或者恒小于等于0),导函数在定义域的某些区间上值大于0而在另一些区间上值小于0。这样我们就有了对参数进行分类的依据。
三、问题举例及解决方案提出
1、问题举例
下面我将结合具体问题来对参数的分类方法加以阐述。
问题:设函数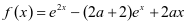 。 (1)当
。 (1)当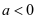 时,讨论函数
时,讨论函数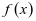 的单调性;(2)若
的单调性;(2)若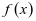 有两个零点,求实数
有两个零点,求实数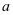 的取值范围。
的取值范围。
解:(1)略(2)解: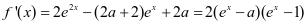
当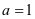 时,
时,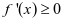 ,
,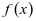 在
在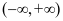 为增函数,
为增函数,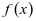 至多一个零点,不合题意;
至多一个零点,不合题意;
当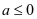 时,
时,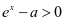 ,由(1)知
,由(1)知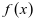 在
在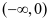 为减函数,在
为减函数,在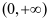 为增函数,故
为增函数,故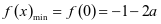 。若
。若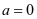 ,则
,则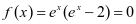 ,
,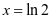 ,
,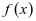 只有一个零点; 若
只有一个零点; 若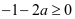 ,即
,即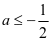 ,则
,则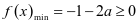 ,此时
,此时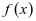 至多一个零点,不合题意; 若
至多一个零点,不合题意; 若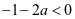 ,即
,即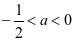 ,则
,则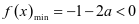 ,又
,又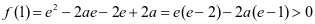 ,且
,且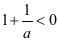 ,
,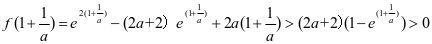 ,说明当
,说明当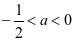 时,
时,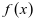 有两个零点;当
有两个零点;当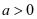 时,令
时,令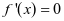 ,则
,则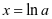 或
或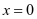 。若
。若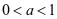 ,则
,则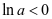 ,
,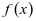 在
在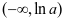 和
和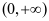 为增函数,在
为增函数,在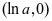 为减函数,
为减函数,
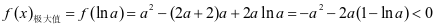 。此时
。此时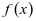 至多一个零点,不合题意;若
至多一个零点,不合题意;若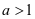 ,则
,则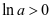 ,
,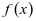 在
在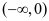 和
和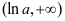 为增函数,在
为增函数,在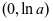 为减函数,
为减函数,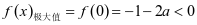 ,
,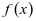 至多一个零点,不合题意; 综上,若
至多一个零点,不合题意; 综上,若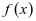 有两个零点,实数
有两个零点,实数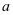 的取值范围为
的取值范围为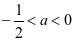 。
。
2、解决方案提出
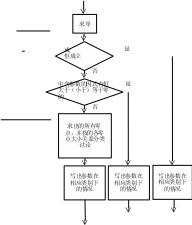 我们将以上解决问题的思维过程归纳为以下几个步骤:
我们将以上解决问题的思维过程归纳为以下几个步骤:
第一步:求导(能直接分解因式则分解因式)
第二步:判断是否有 的情况,当
的情况,当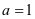 时,
时,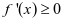 ,……
,……
第三步:判断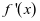 中含参数的因式是否有恒大于等于零(或恒小于等于零)的情况。当
中含参数的因式是否有恒大于等于零(或恒小于等于零)的情况。当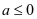 时,
时,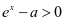 ,……
,……
第四步:求出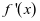 的所有零点,并讨论
的所有零点,并讨论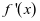 的各零点之间的大小。当
的各零点之间的大小。当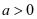 时,令
时,令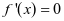 ,则
,则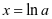 或
或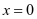 。若
。若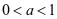 ,则
,则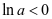 ,……。若
,……。若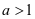 ,则
,则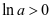 ,……
,……
第五步:综合各种分类情况,写出结果。
根据上面问题的解决流程,我们绘制如右的思维流程图:
四、方法应用
根据以上总结的解题流程,我们来试解一道高考题。
(2017年新课标Ⅰ理科卷)已知函数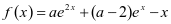 。(1)讨论
。(1)讨论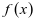 的单调性;(2)若
的单调性;(2)若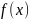
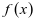 有两个零点,求
有两个零点,求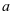 的取值范围。
的取值范围。
解:(1) 第一步:求导(能分解因式则分解因式)
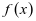 的定义域为
的定义域为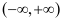 ,
,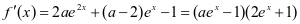
第二步:判断是否有 的情况。若
的情况。若 ,则
,则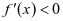 ,所以
,所以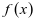 在
在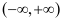 单调递减。
单调递减。
第三步:判断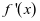 中的因式是否有恒大于等于零(或恒小于等于零的情况)。本题中含参数因式恒小于零的情况无需讨论,在第二步中已有考虑,直接跳过。
中的因式是否有恒大于等于零(或恒小于等于零的情况)。本题中含参数因式恒小于零的情况无需讨论,在第二步中已有考虑,直接跳过。
第四步:若能求出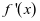 零点则求出所有零点,并讨论
零点则求出所有零点,并讨论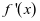 的各零点之间的大小,写出原函数的单调区间;本题中
的各零点之间的大小,写出原函数的单调区间;本题中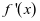 只有一个零点,无需讨论,可直接写原函数的单调区间。若
只有一个零点,无需讨论,可直接写原函数的单调区间。若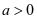 ,则由
,则由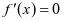 得
得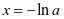 。当
。当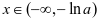 时,
时,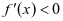 ;当
;当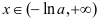 时,
时,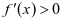 ,所以
,所以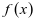 在
在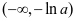 单调递减,在
单调递减,在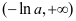 单调递增。
单调递增。
(2)第一步:求导(能分解因式则分解因式)
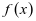 的定义域为
的定义域为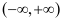 ,
,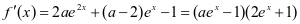 。
。
第二步:判断是否有 的情况,若
的情况,若 ,
,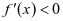 ,所以
,所以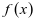 在
在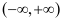 单调递减,
单调递减,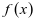 至多有一个零点。
至多有一个零点。
第三步:判断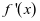 中的因式是否有恒大于等于零(或恒小于等于零的情况)。本题中含参数因式恒小于零的情况无需讨论,在第二步中已有考虑,直接跳过。
中的因式是否有恒大于等于零(或恒小于等于零的情况)。本题中含参数因式恒小于零的情况无需讨论,在第二步中已有考虑,直接跳过。
第四步:若能求出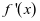 零点则求出所有零点,并讨论
零点则求出所有零点,并讨论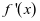 的各零点之间的大小,写出原函数的单调区间;若
的各零点之间的大小,写出原函数的单调区间;若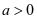 ,由由
,由由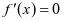 得
得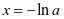 ,
,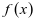 取得最小值,最小值为
取得最小值,最小值为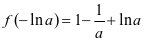 。
。
①当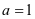 时,由于
时,由于
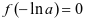 ,故
,故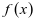 只有一个零点;
只有一个零点;
②当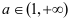 时,由于
时,由于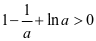 ,即
,即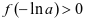 ,故
,故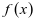 没有零点;
没有零点;
③当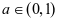 时,
时,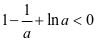 ,即
,即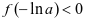 。
。
又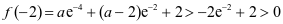 ,故
,故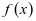 在
在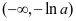 有一个零点。
有一个零点。
而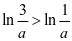 ,且
,且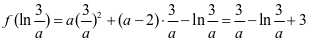
由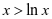 可得
可得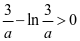 ,则
,则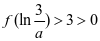 ,故
,故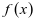 在
在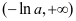 有一个零点。
有一个零点。
综上可得,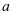 的取值范围为
的取值范围为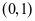 。
。
通过以上问题的解决,我们看到,依据所绘制的思维流程来对参数进行分类,可以非常顺利地使问题得解,而且这样的分类方法,无论是针对函数的单调性讨论问题,还是针对函数的零点存在性问题,都具有很好的适应性。
五、解决方案改进
接下来,我们再来看一道高考题,用上面总结的方法来试解:
(2010年新课标理科卷)设函数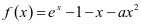 。(1)若
。(1)若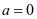 ,求
,求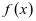 的单调区间;(2)若当
的单调区间;(2)若当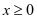 时
时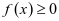 ,求
,求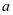 的取值范围。
的取值范围。
解:(1)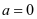 时,
时,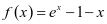 ,
,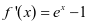 。当
。当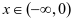 时,
时,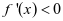 ;当
;当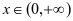 时,
时,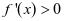 。故
。故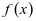 在
在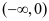 上单调递减,在
上单调递减,在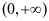 上单调递增。
上单调递增。
(2)第一步:求导(能分解因式则分解因式)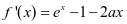 。
。
第二步:判断是否有 的情况。当
的情况。当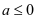 时,
时,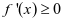 ,
,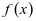 在
在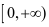 上单调递增,而
上单调递增,而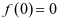 ,故
,故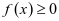 ,满足条件。
,满足条件。
第三步:判断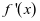 中的因式是否有恒大于等于零(或恒小于等于零的情况)。本题中无分解因式的情况,无需讨论,在第二步中已有考虑,直接跳过。
中的因式是否有恒大于等于零(或恒小于等于零的情况)。本题中无分解因式的情况,无需讨论,在第二步中已有考虑,直接跳过。
第四步:若能求出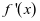 零点则求出所有零点,并讨论
零点则求出所有零点,并讨论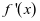 的各零点之间的大小,写出原函数的单调区间;否则回到第一步。本题中
的各零点之间的大小,写出原函数的单调区间;否则回到第一步。本题中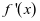 的零点无法直接求出,所以回到第一步,重复执行流程(二次求导,重复进行分类讨论流程)。
的零点无法直接求出,所以回到第一步,重复执行流程(二次求导,重复进行分类讨论流程)。
第一步:求导(能分解因式则分解因式) 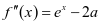 ,
,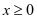 。
。
第二步:判断是否有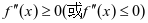 的情况。 当
的情况。 当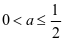 时,
时,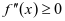 ,
,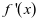 在
在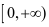 上单调递增。 而
上单调递增。 而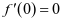 ,故
,故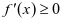 , 又
, 又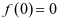 ,故
,故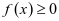 ,满足条件。
,满足条件。
第三步:判断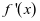 中的因式是否有恒大于等于零(或恒小于等于零的情况)。本题中无分解因式的情况,无需讨论,直接跳过。
中的因式是否有恒大于等于零(或恒小于等于零的情况)。本题中无分解因式的情况,无需讨论,直接跳过。
第四步:若能求出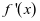 零点则求出所有零点,并讨论
零点则求出所有零点,并讨论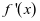 的各零点之间的大小,写出原函数的单调区间;否则回到第一步。当
的各零点之间的大小,写出原函数的单调区间;否则回到第一步。当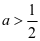 时,
时,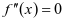 则
则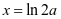 。若
。若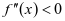 ,则
,则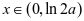 ,即
,即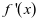 在
在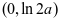 上单调递减,而
上单调递减,而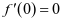 ,故在
,故在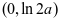
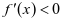 。又
。又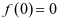 ,故在
,故在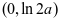
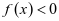 ,不满足条件。
,不满足条件。
第五步:综合各种分类情况,写出结果。
综上可得,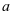 的取值范围为
的取值范围为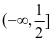
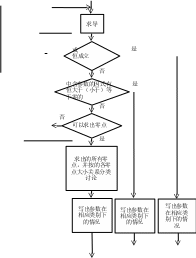 以上问题与前述问题相比,分类更为复杂,因为
以上问题与前述问题相比,分类更为复杂,因为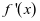 的零点不能直接求出,所有要进行二次求导。从思维流程上来讲,要再一次执行之前的流程,也就形成了循环流程,所以在前述流程图基础上,要进一步修正为有循环体的流程图,如图:
的零点不能直接求出,所有要进行二次求导。从思维流程上来讲,要再一次执行之前的流程,也就形成了循环流程,所以在前述流程图基础上,要进一步修正为有循环体的流程图,如图:
掌握了这个流程图,今后我们就可以结合这个思维流程图来对导数含参数问题中的参数进行准确分类,使问题顺利得到解决。
参考文献:
[1]郝保国。多视角破解高考数学压轴题:函数与导数。杭州:浙江大学出版社,2018。10(2019。3重印):47-48,157-158