基于实测模态的混凝土拱桥有限元模型修正

基于实测模态的混凝土拱桥有限元模型修正

王志兰 1，王潮通讯作者 2,3

1.东南大学建筑设计研究院有限公司，南京 210096； 2.东南大学土木工程学院，南京 210096； 3.pision of Structural Engineering, Luleå university of Technology, Luleå, Sweden

摘要

本文针对混凝土铁路拱桥的特点，提出了一种基于实测模态的有限元模型修正方法。该方法采用精细化壳单元建模，并结合手动修正及非线性算法对模型进行修正。本文引入五种目标函数对模型参数进行优化，基于实测及模拟结果吻合度挑选出其中修正效果较好的目标函数。本文以位于瑞典北部的一座混凝土铁路桥梁—Långforsen桥为例，探讨了该修正方法的准确性和可行性。研究发现，该修正方法提高了有限元模型计算结果与实测响应的吻合度。

1. 概述

据统计，美国境内57.5万座桥梁中约41 %存在明显的结构缺陷，平均每年约有150~200座桥梁被部分或全部破坏。在法国、德国和挪威，存在缺陷的桥梁比例分别为39%、37%和26%^[1]。为针对性对既有桥梁结构进行加固修复，需对其损伤状况进行评估，由于既有桥梁之间差异性，因此寻求有效的评估方法是当务之急。

有限元单元法是一种理论数学模型建立方法，通过建立精确的有限元模型可以准确计算结构的静动态特性，从而对桥梁结构进行健康状态评估。采用有限元单元法进行桥梁评估一般存在误差，因此需要引入修正技术来减小模型误差，以达到应用有限元模型准确评估桥梁健康状态的目的。为准确评估既有桥梁结构的健康状态，本文结合实测模态，提出了一种针对混凝土拱桥的模型修正方法。本文以一座混凝土铁路拱桥—Långforsen桥为例建立了初始有限元模型，并基于本文提出的方法进行修正，将实测响应与修正后有限元计算结果进行对比，验证了混凝土拱桥修正方法的实用性和有效性。

2. 有限元建模

有限单元法是公认的仿真分析方法，但由于建模过程中存在单元选择及简化等各种问题，创建完善的模型仍然是一个难题。为更准确、全面地研究桥梁结构的静动力特性，在综合考虑桥梁结构几何尺寸、材料和边界条件的基础上，本文针对混凝土铁路拱桥提出了一种利用商业软件ABAQUS进行建模的方法。

有限元建模主要包含三方面误差^[2,3]：(1)模型阶次误差，由于有限单元离散造成；(2)模型参数设置误差，如材料属性和杆件几何尺寸误差等；(3)模型结构误差，通常由建模时的简化和假设造成。目前，大多数学者都采用梁单元进行桥梁结构建模。为了提高有限元模型的分析精度，本文采用壳单元建立桥梁结构模型。与空间梁格模型相比，壳单元模型离散度明显减小，可大大减少模型的阶次误差。

3. 模型修正方法

有限元模型修正是基于动静态响应修正模型参数(如刚度、质量、边界条件等)，使模型预测值接近试验值的方法。因此，目标函数的确定、待修正参数的选择是参数化模型修正的三个关键问题。采用精细化壳单元和手动修正可以避免一些误差，但并不能完全消除。为进一步减小模型误差，从而准确的评估桥梁结构的健康状况，本文提出一种基于实测模态的修正方法，首先建立初始模型，随后手动修正得到先验模型，通过灵敏度分析后选取修正参数，再经由目标函数进行参数修正，最终得到修正后模型。

1. 初步手动修正

由于理想化的有限元模型的预测与实测之间的差异，在模型非线性修正之前可以进行初步的人工调整。例如，通过比较实测和预测的多阶特征频率的吻合度，对模型刚度分布进行初步修整，得到先验模型。

2. 模型参数选择

参数的选择是模型修正的决定因素，修正参数的选择主要有两种方法，一种是依靠工程经验，另一种是基于参数的灵敏度分析。选取的参数必须具有较高的灵敏度，灵敏度较低的参数会产生额外的模型误差。

灵敏度从数学上可以理解为多元函数自变量的偏导数，一阶敏感性对应一阶偏导数或一阶微分。它可以表示为：

其中λ为特征值，p为模型参数。

混凝土铁路拱桥的模型参数一般包括拱和立柱的边界条件、主拱的弹性模量、混凝土构件的密度、主跨和边跨的约束等。具体选择需要参照上述原则。

3. 目标函数

目标函数是反映有限元预测值与实测值之间差异的误差函数，模型参数优化是使目标函数值最小化的过程。在基于动力响应的有限元模型修正过程中，可以根据预测的和理论的固有频率、位移、加速度、应变等建立目标函数。通常用两个数据集之间的差异来表示误差，但考虑到普适性，目标函数应该是无量纲的，随后出现了相对差之和或相对差之平方的函数形式，如和，Q. W. Zhang等^[4]发现分母对相对差的影响很大，因此建议用标准差代替，如和。如下所示：

式中，和分别为是第j个时间点或位置点的预测和实测响应，n是测量响应的个数，是实测与预测响应的方差，。

4. 案例分析

1. 工程概况

Långforsen桥位于瑞典北部，如图1所示，该桥建于1960年。由于铁路运输的需要，需将轴重由22.5t升级至更高轴重，因此本文以该桥为研究对象，采用FEM评估该桥的实际承载能力。为了测得Långforsen桥在移动列车作用下的模态，验证桥梁有限元模型的合理性，瑞典铁路局和瑞典吕勒奥理工大学合作进行了桥梁模态关键点加速度的现场实测

^[5,6]。

图1. Långforsen桥

2. 有限元模型

为了更准确、全面地研究Långforsen桥的动力特性，本文基于有限元软件Abaqus建立了Långforsen桥的有限元模型^[7]，如图2所示。该桥的有限元模型中16根立柱与轨道采用梁单元建立，道砟采用离散的质量点建立，柔性边界条件采用弹簧单元建立，主体部分包含桥面板、主拱等全部采用壳单元建立。初始有限元模型中混凝土弹模根据取芯试验测得，混凝土弹性模量的平均值为32500 MPa；钢筋混凝土密度取为2.6 t/m3；土壤变形模量根据经验取为25 kg/cm³。

图2. 有限元模型

3. 有限元模型修正

在采用目标函数修正前，通常需要通过初步估计来进行手动修正，以获得合理的近似值，避免后期修正时迭代过程发散，从而得到先验模型。为了提高与实测响应的吻合度，可以在比较预测和测量本征频率的基础上进行手动细化。

本文采用子空间迭代法提取初始模型的前七阶模态特征值，见表1。通过对前7个模态的实测值与初始分析值的比较，得出频率值均低于实测值的结论。由于特征频率与刚度或质量之间的关系，在手动修正的过程中，弹性模量可以增加，密度也可以减小。

表1. Långforsen桥实测和初步模型计算特征值

本案例选取了桥梁结构的模态作为修正依据，确定了以弹簧刚度表示的边界条件、主体结构弹性模量、混凝土密度、立柱刚度作为初步优化参数。经过灵敏度分析发现桥墩的弹簧刚度和立柱的刚度对修正结果的影响较小，因此后续修正中不予选择该参数，弹性模量、混凝土密度、土壤变形模量和桥墩的弹簧刚度的敏感性分析结果如图3所示。立柱的刚度与弹簧的结果相似桥墩的刚度，因此未做赘述。

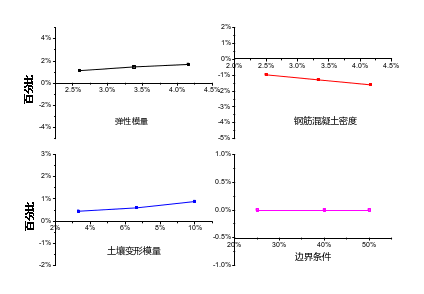
图3. 参数的灵敏度分析

本文分别用上述5种目标函数对参数进行优化，并进行误差分析，表2中总结了五种目标函数修正后平均误差。结果表明，按～进行优化可减小动态响应的平均误差，但存在差异。通过以上分析可以得出结论：当目标函数以相对差的形式用时程响应进行优化时，由于局部响应的数量级不同，且这种形式仅限于分母，可能导致优化的不确定性；同一目标下，高阶优化比低阶优化效果好。可以明显看出，目标函数的优化效率优于其它目标函数。

表2. 有限元模型平均误差

经由上述修正后，实测与预测模态特征值的对比如表3所示，证明了针对混凝土铁路拱桥有限元模型修正方法的准确性。

表3. 实测模态与修正后模型计算值对比

5. 结论

本文提出了一种基于实测模态的混凝土铁路拱桥有限元模型修正方法，并以Långforsen大桥为例进行了验证。整个修正过程强调初步的手动和基于目标函数的参数优化。前者主要基于工程判断，后者涉及模型参数及目标函数选择等。本文采用五种目标函数对参数进行优化，最终选出适用于本文桥梁结构的最优目标函数。本文选取前七阶模态的预测值与实测值对比，通过灵敏度分析选取3结构参数用于有限元修正。修正后的混凝土铁路拱桥有限元模型预测结果与实测值吻合度较好，为既有桥梁结构的承载力评估、损伤检测和健康监测提供了可靠的方法。

参考文献：

[1] Woodward R, Cullington D, Daly A, et al. Bridge management in Europe (BRIME)-Deliverable D14-Final Report[J], 2001.

[2] Mottershead J E, Friswell M I. Model Updating In Structural Dynamics: A Survey[J]. Journal of Sound & Vibration, 1993, 167(2): 347-375.

[3] Brownjohn J M W, Dumanoglu A A, Severn R T. Ambient vibration survey of the fatih sultan mehmet (second Bosporus) suspension bridge[J], 1992, 21(10): 907-924.

[4] Zhang Q, Chang T-Y P, Chang C C. Finite-element model updating for the Kap Shui Mun cable-stayed bridge[J]. Journal of Bridge Engineering, 2001, 6(4): 285-293.

[5] Wang C, Zhang J, Tu Y, et al. Fatigue assessment of a reinforced concrete railway bridge based on a coupled dynamic system[J]. Structure and Infrastructure Engineering, 2020, 16(6): 861-879.

[6] Sabourova N, Grip N, Tu Y, et al. Railway Concrete Arch Bridge over Kalix River at Långforsen: Dynamic Properties and Load-Carrying Capacity. Luleå University of Technology, 2019.

[7] Wang C, Wang Z, Zhang J, et al. FEM based research on the dynamic response of a concrete railway arch bridge[C]. 19th IABSE Congress Stockholm, 21-23 September 2016, 2016: 2472-2479.