陆军航空兵学院 100000
摘要
中小型企业贷款还款能力低,信用风险大等特点降低了银行在中小企业贷款方面的积极性。为了使银行在贷款风险足够小的情况下,得到最高的回报。银行需要对企业进行量化分析,针对企业的信誉度、规模、发展前景等众多因素,最终制定最优的信贷策略。本文通过数学建模,依据现有的数据,并参考实际的情况,为银行制定最优的信贷策略。
针对所给的材料(附件1、附件3)对数据进行处理与分析。对附件1中的企业进行统计分析,从横向与纵向对比企业的规模实力、近年来的发展趋势以及企业发展的稳定性。建立主成分分析模型对企业的各个指标进行客观的分析,得出各个指标对银行向企业贷款的权重,从而得到企业的综合评分。根据各个企业的综合评分,为银行制定相应的信贷策略。
关键词:银行信贷,统计分析,目标规划模型,退火算法。
1问题重述
某银行对确定要放贷企业的贷款额度为![]() 元;年利率为4%~15%;贷款期限为1年。附件1~3分别给出了123家有信贷记录企业的相关数据、302家无信贷记录企业的相关数据和贷款利率与客户流失率关系的2019年统计数据。该银行请你们团队根据实际和附件中的数据信息,通过建立数学模型研究对中小微企业的信贷策略,主要解决问题:对附件1中123家企业的信贷风险进行量化分析,给出该银行在年度信贷总额固定时对这些企业的信贷策略。
元;年利率为4%~15%;贷款期限为1年。附件1~3分别给出了123家有信贷记录企业的相关数据、302家无信贷记录企业的相关数据和贷款利率与客户流失率关系的2019年统计数据。该银行请你们团队根据实际和附件中的数据信息,通过建立数学模型研究对中小微企业的信贷策略,主要解决问题:对附件1中123家企业的信贷风险进行量化分析,给出该银行在年度信贷总额固定时对这些企业的信贷策略。
2模型假设
假设所给数据客观真实,具有可靠性;
假设所给数据中各企业每年的发票数是完整的;
3符号说明
| 2017年公司净利润 |
| 2018年公司净利润 |
| 2019年公司净利润 |
| 2017、2018及2019年公司净利润之和 |
| 方差 |
| 利润增长率 |
| 原始的数据 |
| 协方差矩阵 |
| 特征值 |
| 特征向量 |
4问题分析
4.1 问题一的分析
问题一要求对附件1中123家企业的信贷风险进行量化分析,给出该银行在年度信贷总额固定时对这些企业的信贷策略。针对所给的材料(附件1、附件3)对数据进行处理与分析。首先,查看数据的完整度并剔除掉数据中的奇异值、剔除掉对企业实力、信誉度无任何影响的数据(例如,各个企业中的作废发票),从而简化模型。其次,对附件1中的企业进行统计分析,从横向与纵向对比企业的规模实力、近年来的发展趋势以及企业发展的稳定性。最后,建立主成分分析模型对企业的各个指标进行客观的分析,得出各个指标对银行向企业贷款的权值,从而得到企业的综合评分。根据各个企业的综合评分,为银行制定相应的信贷策略。
5模型建立与求解
5.1 问题一模型建立与求解
5.1.1 数据预处理
在问题一的求解中,通过对附件1数据的分析,首先,由于银行内部根据企业的实际情况人工评定,银行对信誉评级为D的企业原则上不予放贷。因此,在对附件1进行分析时,首先将信誉评级为D的企业进行了数据的剔除,从而得到信誉等级为A、B、C的企业。另外,一部分企业在为交易活动开具发票后,因故取消了该项交易,使发票作废,或为交易活动开具发票后,企业已入账记税,之后购方因故发生退货并退款,此时,需开具的负数发票。这一部分数据会对整体的数据分析造成干扰,因此,剔除了附件1中123个企业存在作废发票以及负数发票的数据。
由于需要评估制定银行在年度信贷总额固定时对这些企业的信贷策略。因此,考虑了企业信誉评级、企业营业规模、企业发展稳定性、企业利润增长率4个因素,从而方便银行在对这些企业进行信贷时制定策略。其中,企业信誉评级分别为:
![]() (1)
(1)
企业营业规模的评判标准为:
![]() (2)
(2)
求解2017年至2019年净利润的方差,从而量化企业发展稳定性指标:
![]() (3)
(3)
企业利润增长率为:
![]() (4)
(4)
且由于附件1中存在![]() ,因此,针对这一类特殊情况,采用以下公式对企业利润增长率进行求解:
,因此,针对这一类特殊情况,采用以下公式对企业利润增长率进行求解:
![]() (5)
(5)
根据公式(1)—公式(5),分别量化了企业信誉评级、企业营业规模、企业发展稳定性、企业利润增长率4个评判指标,其量化指标如附件二所示。
5.1.2 建立主成分分析(PCA)数学模型
步骤一:对原始数据进行标准化处理;
基于附件二中预处理数据,为了方便计算机的处理计算,首先对原始数据进行标准化处理;
![]()
步骤二:计算协方差矩阵C;
对标准化后的数据x求协方差矩阵,即:
![]()
步骤三:计算协方差矩阵C的特征值和特征向量;
根据下式求得矩阵C的特征值![]() ,再将特征值
,再将特征值![]() 由大到小排列,根据4个指标的具体情况,选择最大的前m个,同时选择最大的前m个特征值对应的特征向量,组成
由大到小排列,根据4个指标的具体情况,选择最大的前m个,同时选择最大的前m个特征值对应的特征向量,组成![]() 的矩阵。
的矩阵。
![]()
步骤四:原始数据的降维;
根据标准化后的数据以及特征向量组成的矩阵k,利用下式可求得降维后的数据。
![]()
5.1.3 PCA模型求解及结果分析
为了更加直观的反应银行在对企业进行信贷时的策略,将利用PCA对附件2中的四个量化指标进行主成分分析,结果分析如下:
表5.1.1 四个指标相关性分析
指标相关性 | 企业利润增长率 | 企业发展稳定性 | 企业信誉评级 | 企业营业规模 |
企业利润增长率 | 1.0000 | 0.0036 | 0.1214 | -0.0049 |
企业发展稳定性 | 0.0036 | 1.0000 | -0.0600 | 0.5082 |
企业信誉评级 | 0.1214 | -0.0600 | 1.0000 | -0.0667 |
企业营业规模 | -0.0049 | 0.5082 | -0.0667 | 1.0000 |
如表5.1.1所示,企业营业规模与企业发展稳定性的数据具有较大的相关性,相关性系数为0.5082,因此,结合实际情况可得,若企业在长期的经营中净利润不断上升,则意味着该企业经营模式的优越性以及公司在面对风险时具有的稳定性。
表5.1.2 四个指标主成份分析
编号 | PC1 | PC3 | PC2 | PC4 | 累计贡献率 |
1 | -0.0431 | -0.6850 | 0.7272 | 0.0102 | |
2 | 0.6944 | 0.0698 | 0.1167 | -0.7066 | |
3 | -0.1779 | 0.7216 | 0.6690 | 0.0070 | |
4 | 0.6959 | 0.0724 | 0.0995 | 0.7075 | |
贡献率 | 38.11% | 27.79% | 21.81% | 12.29% | 100% |
针对问题一的分析,分别采取了企业信誉评级、企业营业规模、企业发展稳定性、企业利润增长率4个指标进行量化分析。如表5.1.2所示,上述4个量化指标可以由4个主成分表示,其中第一主成分贡献率为38.11%,该成分的主要贡献主要来自于第四个指标,即企业营业规模,因此,进一步说明,企业营业规模(净利润)将在银行对其进行信贷决策时占有较大的比重,同时,第一主成分也与企业发展稳定性具有很大的关系。因此,可以说明当银行在对企业进行信贷决策时,一个企业的企业营业规模(净利润)以及长期发展的稳定性将占有38.11%的比重。第二主成分贡献率为27.79%,其主要贡献来自于第三个指标(企业信誉评级),通过分析可以得出,当银行对企业的企业营业规模评估完成后,企业信誉评级其比重为27.79%。即银行通过将企业的信誉按照27.79%的占重比进行评估。第三主成分的贡献率为21.81%,其主要贡献来自于第一个指标(企业利润增长率),即当银行对企业的营业规模以及企业信誉评估完成后,企业利润增长率将作为第三个重要评估因素,决定银行对企业进行信贷的额度。在实际的银行信贷中,银行同样在对企业近年的营业状况以及企业的信誉评估完成后,同样会考察企业近年来的增长率,从而来间接的评估企业未来的发展空间。从而使得银行在信贷中收益最优,且客户流失率最低。第四主成分的贡献率为12.29%,其主要贡献来自于企业发展稳定性。根据主成分分析,银行在评估企业稳定性时将按照12.29%的权重进行评估。
综上所述,银行在年度信贷总额固定时,首先按照38.11%的比重对企业营业规模(净利润)进行评估,其次,按照27.79%、21.81%的占重分别评估企业信誉评级和企业利润增长率,最后,银行将按照12.29%的比重评估企业发展稳定性。银行根据以上的评分权重,将对各个企业的信贷风险p进行评分,为银行制定相应的信贷策略。
5.1.4建立双目标规划模型
1)数据拟合
为了得到客户流失率关于贷款年利率的拟合数据,采用二次拟合,对题目附件3中的数据进行拟合。
2)建立双目标规划模型
首先考虑信贷风险 p以及银行的收益最大化,使如下式子达到最大:
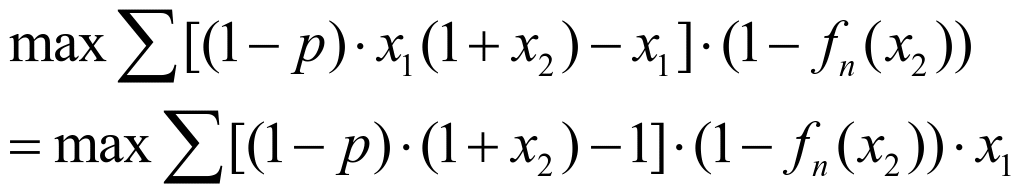 (6)
(6)
![]() (7)
(7)
其中:
![]() :为达到不会违规的概率,
:为达到不会违规的概率,![]() :违规概率;
:违规概率;
![]() :对每一个企业的投资金额;
:对每一个企业的投资金额;
![]() :对每一个企业投资的利率;
:对每一个企业投资的利率;
![]() :求出的客户流失率关于贷款年利率的拟合函数。
:求出的客户流失率关于贷款年利率的拟合函数。
![]() :挽留的客户比例,失去的那一部分表示不赚钱。
:挽留的客户比例,失去的那一部分表示不赚钱。
由于公式(7)是关于![]() 的函数,因此,在保证
的函数,因此,在保证![]() 一定的情况下,只要使该式最大,即可保证公式(6)达到最大时。
一定的情况下,只要使该式最大,即可保证公式(6)达到最大时。
通过建立模拟退火算法,求解公式(7),算法原理图如图5.1.4所示,其建立步骤为:
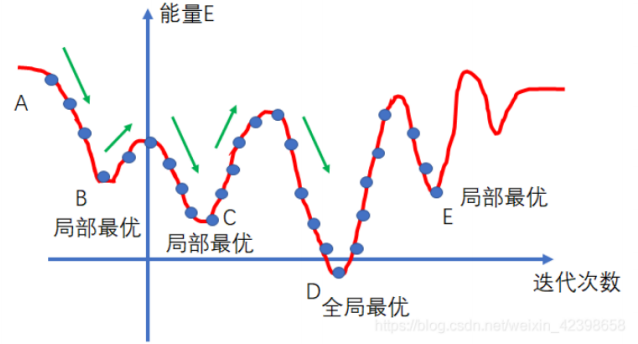
图5.1.4 模拟退火算法原理图
![]() ,在解空间中随机生成一个初始解
,在解空间中随机生成一个初始解![]() ,作为搜索起始点
,作为搜索起始点![]() ,计算搜索点S对应的目标函数值
,计算搜索点S对应的目标函数值![]() ;
;
![]() ,在 S 附近随机生成一个新解
,在 S 附近随机生成一个新解![]() ,计算
,计算![]() 对应的目标函数值
对应的目标函数值![]() ;
;
若![]() ,则搜索点S移动到解
,则搜索点S移动到解![]() 的位置,然后重复步骤b;
的位置,然后重复步骤b;
若![]() ,与爬山算法不同,搜索点此时并没有完全拒绝解
,与爬山算法不同,搜索点此时并没有完全拒绝解![]() ,而有一定的概率p接收新解。利用程序生成一个
,而有一定的概率p接收新解。利用程序生成一个![]() 之间的随机数r,如果
之间的随机数r,如果![]() ,说明这个概率为p的把握成立,则搜索点S移动到
,说明这个概率为p的把握成立,则搜索点S移动到![]() 的位置,反之S不移动,然后重复步骤b。
的位置,反之S不移动,然后重复步骤b。
利用MATLAB即可求得(7)式,因此,将公式(6)转化为![]() ,其中c由模拟退火算法可求得。
,其中c由模拟退火算法可求得。
6模型评价与推广
对附件1中的企业进行统计分析,从横向与纵向对比企业的规模实力、近年来的发展趋势以及企业发展的稳定性。最后,建立主成分分析模型对企业的各个指标进行客观的分析。同时,考虑到银行收益的最大化,对附件3进行拟合分析,建立目标规划模型,并利用模拟退火算法进行求解。最终得到银行对附件1中各个企业贷款的年利率。保证了银行的有效收益。
优点在于: 通过对附件1中的各个企业进行统计分析,并建立主元分析模型,可以很清晰的看出企业的各项指标对信贷的影响。并且通过建立目标规划模型,可以有效的得到银行对各大企业设定的年利率,并制定最优的信贷策略,保证银行的效益。
缺点在于: PCA算法无参数调节,可能会的得不到预期的结果,另外,仅仅通过特征值分解有一定的局限性。
参考文献
李强,赵伟.MATLAB数据处理与应用[M],国防工业出版社.2001
李毅. 中小企业信贷融资信用担保缺失研究[J]. 当代经济研究, 2008, 000(010):53-57.
糜仲春, 申义, 张学农. 我国商业银行中小企业信贷风险评估体系的构建[J]. 金融论坛, 2007(3).
萧嵘, 王继成, 张福炎. 支持向量机理论综述[J]. 计算机科学, 2000, 27(3):1-3.
杨珩, 崔洋. 基于Elman神经网络的上海港货物吞吐量预测研究[J]. 交通科技, 2012, 000(004):133-136.
李晓黎, 刘继敏, 史忠植. 基于支持向量机与无监督聚类相结合的中文网页分类器[J]. 计算机学报, 2001(01):62-68.
5