浅析洛必达法则及其应用

杨付贵

广州工商学院通识教育学院 广东 佛山 528138

摘要：洛必达法则是高等数学中求不定式极限的一种行之有效的简便方法，大部分未定式极限用洛必达法则求解非常方便，但并非所有的未定式极限都能用洛必达法则求解，同时有部分非未定式极限也可以考虑用洛必达法则的推广求之。本文主要阐述使用洛必达法则应注意的事项，以及点滴体会。为读者能够较正确深入，清晰的理解和掌握洛必达法则及其应用，提供一些思路，方法和参考。如有不当之处，望读者给予批评指正。

关键词: 洛必达法则；求极限方法；不定式极限；洛必达法则推广

我 们知道，如果在自变量的某一个变化过程中，函数 都趋向于零或无穷大，

这时 可能存在，也可能不存在，通常，把这种形式的极限叫做未定式，并分别记作

或 型，洛必达法则就是为解决这类极限而提供的一种行之有效的简便方法。

洛 必达法则：（1）当 （或 ）时， 都趋向于零或无穷大；（2）在

的某去心邻域内（或当 时）， 可导，且 ；（3） 存在或为无穷大。 则

。

注1：此定理的证明见教材[2]

注2：如果 仍为 或 型，而 存在或为无穷大，则

，以此类推，但在整个求解过程的每一步求导前，都要检查一下是否为 或

型，切勿乱用。

例1： （不再是未定式，不能再使用洛必达法则，否则将导致错误）

注3：要及时化简极限号后面的分式，尽可能的利用等价代换和已知的几个重要极限。

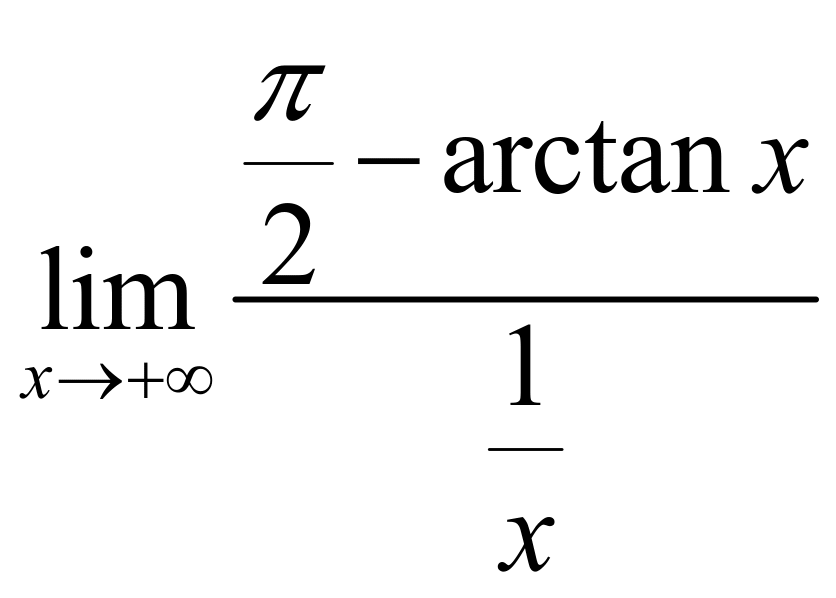
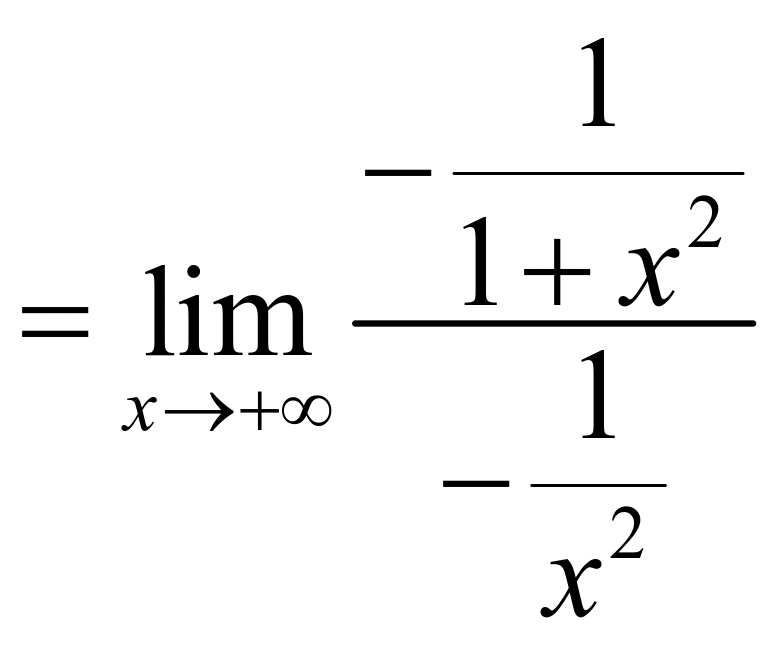
例2： （利用已知 的重要极限）

例3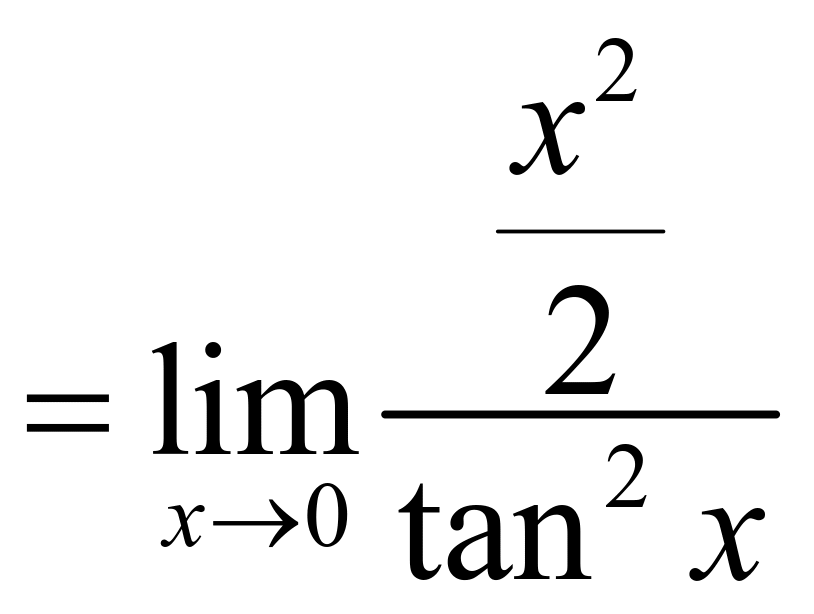： （虽然极限仍是 型未定式，但我们没有接着用洛必达法则，而是利用了等价无穷小量代换，简化了计算过程） （利用已知 的重要极限）

注 4：洛必达法则只对 或 型极限适用，对于其它类型的不定式，应先化成这两种形式之一，再用。

例 4： （此极限是 型未定式，应先化成 或 型，再用洛必达法则）

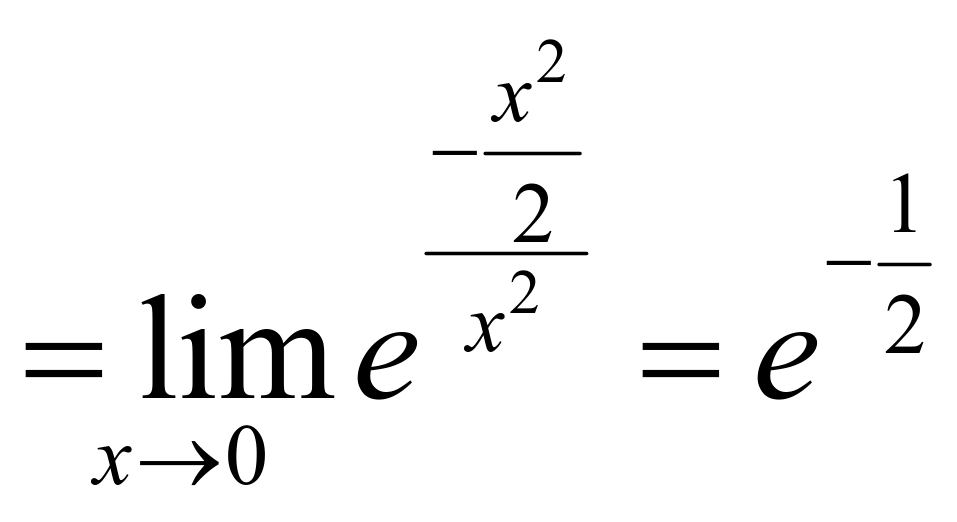
注 5：洛必达法则（ 型未定式极限）的推广：（1）当 （或 ）时， 趋向无穷大；（2）在 的某去心邻域内（或当 时）， 可导，且 ；（3）

存在或为无穷大。 则 。

洛必达法则的推广与洛必达法则相比，对分子上的函数的限制条件减弱了， 它可以有极限，也可以无极限，因此其应用亦拓宽了。它的证明见《数学分析选讲》（刘三阳、于力、李广民编）。

例5：_{（对于，是否趋于无穷大，情形不明，但由广义洛必达法则可得）}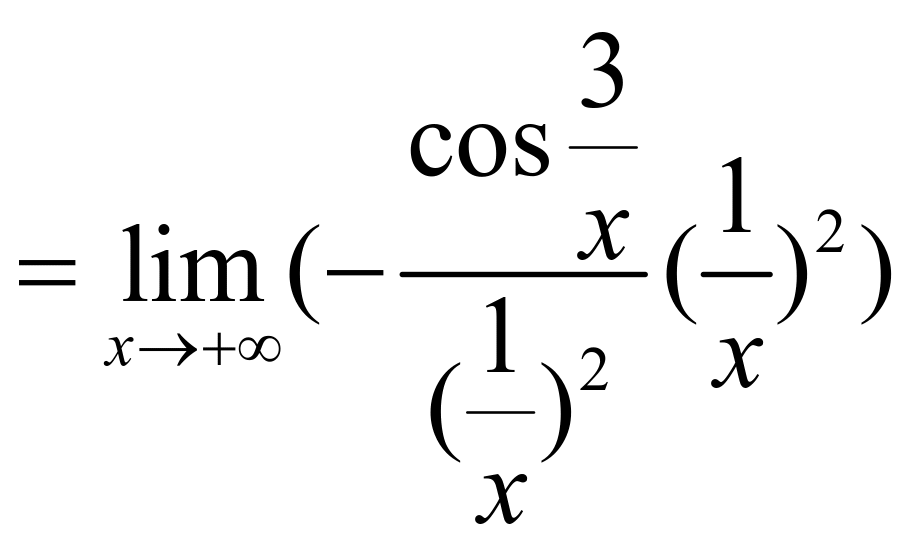

注6：洛必达法则（包括洛必达法则的推广）的条件仅是结论成立的充分条件，不是必要条件。

例6：误解：因为 不存在，所以 不存在。

正确解法如下：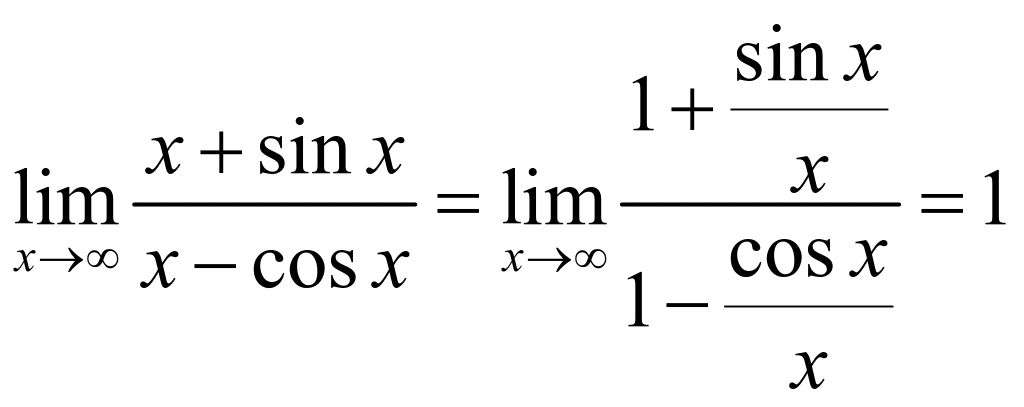

注7：洛必达法则使用误区

（1）由于用洛必达法则求未定式极限非常方便，有时不是未定式极限也用洛必达法则求之。

例7：误解：

正确解法如下：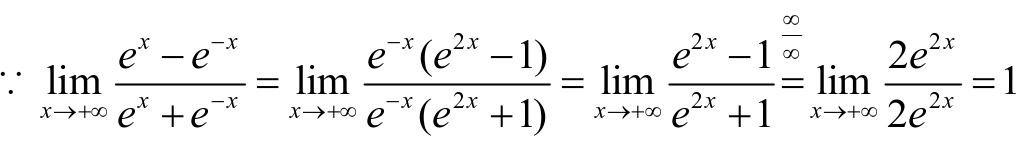

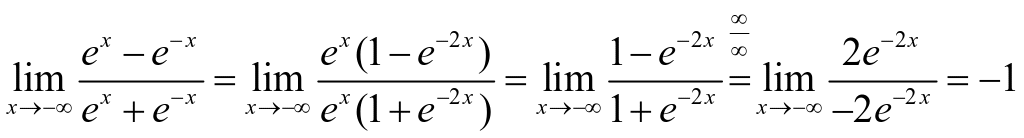
不存在。

（2）洛必达法则是将极限 转化为极限 来求，而有时会误将极限

转化为 来求。

（3）洛必达法则求极限有时会出现循环现象，使问题陷入误区，无法求解。

例8： （回到原题，出现循环.正确解法见例7）。

（4）数列极限用洛必达法则直接求之也是洛必达法则使用过程中的一大误区。

例9：误解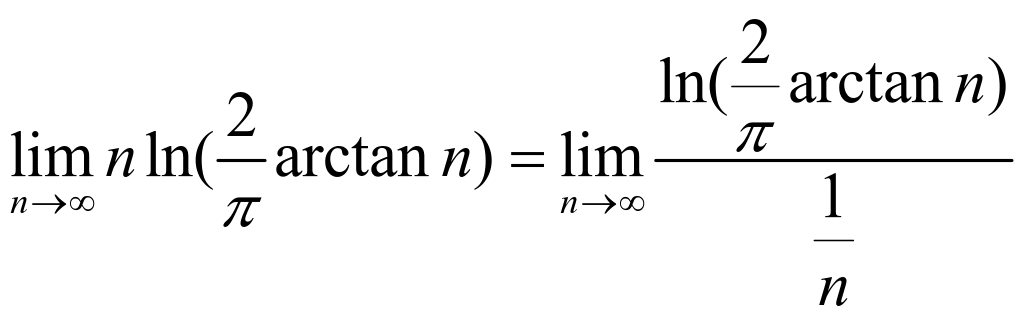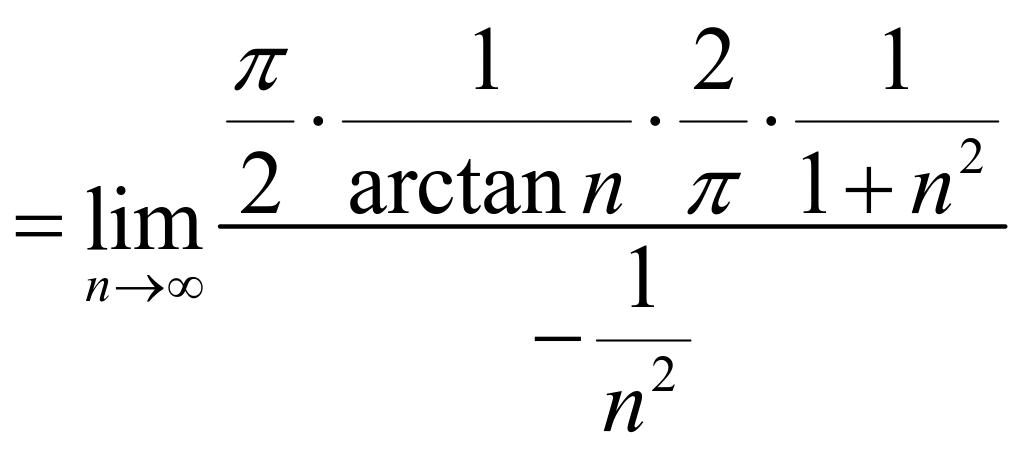： （*） （误解错在(*)式，极限虽然是 型极限，但n是离散变量，不能求导，虽然结果正确，但解题过程不对）。

正确解法：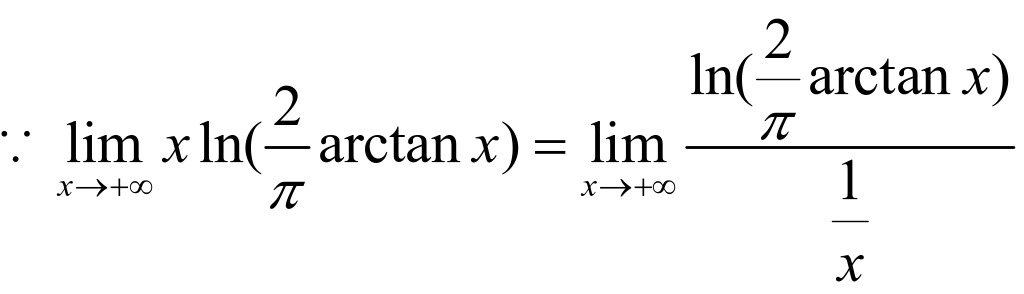

, .

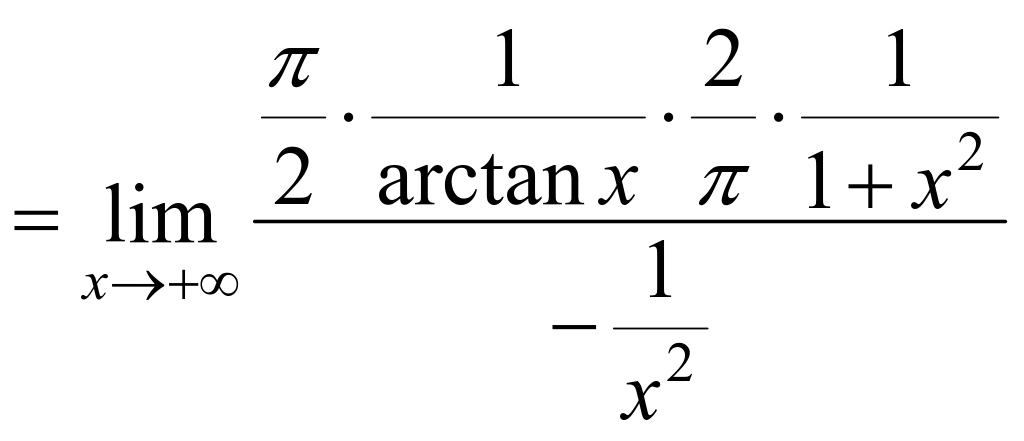
参考文献

[1] 赵秀.洛必达法则及其推广的应用[J].科教导刊

[2] 刘三阳,于力,李广民.数学分析选讲.科学出版社,2007.

[3] 《高等数学》（第七版）上、下册，同济大学数学系编，高等教育出版社

[4] 《高等数学例题与习题》 同济大学高等数学教研室编，同济大学出版社

作者简介：杨付贵（1957.5.26）男，天津人，副教授。从事最优化方法研究。