浅谈利用牛顿运动定律解决弹簧类问题

浅谈利用牛顿运动定律解决弹簧类问题

忻永立

宁波市五乡中学 浙江 宁波 315000

摘要：由于弹簧类问题涉及的知识点较多，综合性也较强，因此一直是高考中考查的重点和难点之一。但无论是哪一种类型的弹簧问题，弹簧的形变量或位移，往往是解决问题的突破口。

关键词：牛顿运动定律、弹簧

在高考试题中，我们碰到的弹簧一般都是“轻弹簧”，而“轻弹簧”是一种常见的理想化物理模型。由于“轻弹簧”质量不计，其所受的弹力一定处处大小相等，均等于弹簧两端的受力。

例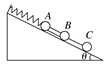 1、如图所示，A、B、C三个小球的质量均为m，轻质弹簧一端固定在斜面顶端，另一端与A球相连，A、B间固定一个轻杆，B、C间由一轻质细线连接．已知倾角为θ的斜面光滑且固定在地面上，弹簧、轻杆与细线均平行于斜面，初始时系统处于静止状态．则细线被烧断的瞬间，下列说法正确的是(　　)

A．B球的受力情况未变，加速度为零

B．A、B两个小球的加速度方向均沿斜面向上，大小均为gsin θ

C．A、B间杆的拉力大小为mgsin θ

D．C球的加速度方向沿斜面向下，大小为gsin θ

[解析]细线烧断前，对A、B、C组成的整体进行受力分析，可求得弹簧弹力F＝3mgsin θ，细线烧断的瞬间，弹簧弹力不变，对A、B组成的整体进行受力分析，有3mgsin θ－2mgsin θ＝2ma_AB，a_AB＝gsin θ，方向沿斜面向上，对B进行受力分析，有F_T－mgsin θ＝ma_AB，轻杆拉力F_T＝mgsin θ，故A、B错误，C正确；对C进行受力分析，由牛顿第二定律得：mgsin θ，mgsin θ＝ma_C，a_C＝gsin θ，方向沿斜面向下，D正确．

点评 本题的关键是物体的加速度不变，利用牛顿第二定律解决弹簧的瞬时加速度问题。

例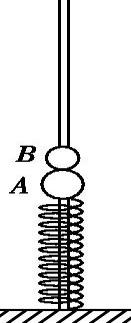 2、足够长的光滑细杆竖直固定在地面上,轻弹簧及小球A、B均套在细杆上,弹簧下端固定在地面上,上端和质量为m₁=50 g的小球A相连,质量为m₂=30 g的小球B放置在小球A上,此时A、B均处于静止状态,弹簧的压缩量x₀=0.16 m,如图所示.从t=0时开始,对小球B施加竖直向上的外力,使小球B始终沿杆向上做匀加速直线运动.经过一段时间后,A、B两球分离;再经过同样长的时间,B球距其出发点的距离恰好也为x₀.弹簧的形变始终在弹性限度内,重力加速度g取10 m/s².求:

(1)弹簧的劲度系数k;

(2)整个过程中小球B加速度a的大小及外力F的最大值.

[解析] (1)根据共点力平衡条件和胡克定律得 (m₁+m₂)g=kx₀

解得k=5 N/m.

(2)设经过时间t,小球A、B分离,此时弹簧的压缩量为x, 对小球A,有

kx-m₁g=m₁a x₀-x=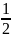at²

对小球B,有 x₀=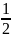a(2t)²

当B与A相互作用力为零时,F最大,设为F_m

对小球B,有F_m-m₂g=m₂a

解得a=2 m/s²,F_m=0.36 N.

点评 胡克定律F=kx中x为弹簧的形变量，与物体相连时x在某些情况下亦即物体的位移，这是解题的关键。

例3如图所示，劲度系数为k的轻弹簧的一端固定在墙上，另一端与置于水平面上质量为m的物体接触（未连接），弹簧水平且无形变。用水平力F缓慢推动物体，在弹性限度内弹簧长度被压缩了x₀，此时物体静止。撤去F后，物体开始向左运动，运动的最大距离为4x₀。物体与水平面间的动摩擦因数为μ，重力加速度为g。则

A．撤去F后，物体先做匀加速运动，再做匀减速运动

B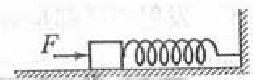 ．撤去F后，物体刚运动时的加速度大小为 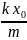－μg

C．物体做匀减速运动的时间为2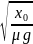

D．物体开始向左运动到速度最大的过程中克服摩擦力做的功为μmg（x₀－ ）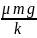

解析 撤去F后，在物体离开弹簧的过程中，弹簧弹力是变力，物体先做变加速运动，离开弹簧之后做匀变速运动，故A错；刚开始时，由kx₀-μmg=ma可知B正确；离开弹簧之后做匀减速运动，减速时间满足3x₀=a₁t₂/2，a₁=μg则t=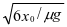 ，从而C错；速度最大时合力为零，此时弹簧弹力F=μmg=kx，x=μmg/k，所以物体开始向左运动到速度最大的过程中克服摩擦力做的功为 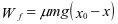= 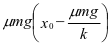，D正确。

点评 本题就是根据物体速度最大时弹力等于摩擦力，根据此时弹力的大小来确定弹簧的压缩量，求出物体运动的位移，从而求出克服摩擦力做的功。

总之，利用牛顿运动定律解决弹簧类问题，要始终抓住了：两个状态———初态和末态；一个过程———弹簧的压缩量不断恢复的过程中。“两个状态,一个过程”,是分析这类题目的关键，把握住这一点，一切都会迎刃而解。