:慈溪市宗汉锦纶初级中学
一、试题呈现
如图1，BC=2，A为半径为1的⊙B上一点，连结AC，在AC上方作一个正三角形ACD，连结BD，则BD的最大值__________。
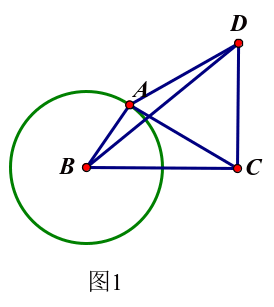
图1
这是九年级区域数学检测中的一道试题。此题是某一动点到已知定点距离的最值问题，涉及点的轨迹。常规思路是运用描点实验法得到猜想，再进行逻辑论证。
解法探究
实验猜想，逻辑论证
如图2，由描点实验法得到D1、D2、D3猜测点D的轨迹是一个圆，假设圆心为O，连结OB、OD、OC，不难发现△OBC与正△ACD构成全等三角形。根据猜测构图，以BC为边，在其上方作正△OBC，连结OD，易证△ABC≌△DOC，则DO=AB=1，其中O为定点。由此可知，动点D在以O为圆心，半径为1的圆上，由此可得BD最大值为3。
同理在BC下方作正△OBC， 或在AB左侧作正△OBA， 或在AB右侧作正△OBA， 都可利用构造两个三角形全等得解。
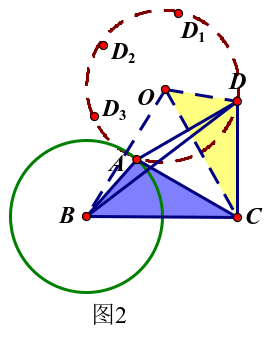
图2
引申推广
推广1：把试题条件正△ACD改为正方形ACDE、正五边形ACDEF正n边形ACDEF…（图3），其余条件保持不变，求BD的最大值？情形又如何呢？
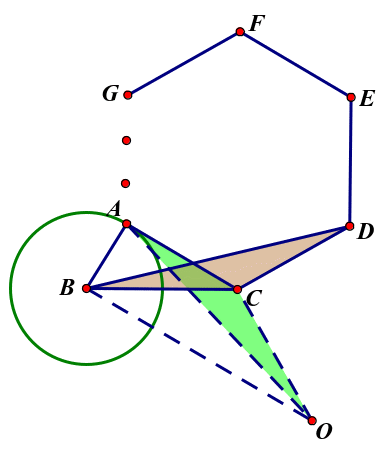
当出现正n边形ACDEF…时，如图8，在BC下方作等腰Rt△BCO,使CO=BC=2，∠BCO=
，连结AO，得BO=4Sin
，易证△ACO≌△DCB，得BD=AO，由此AO最大值为4Sin
+1，即 BD最大值为4Sin
+1。
小结：推广1的问题还是利用构造两个三角形全等解决。
图3
推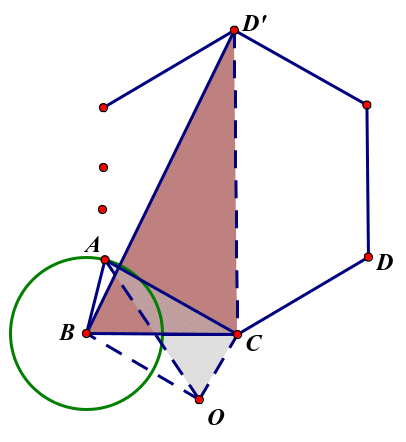
广2：把试题问题求BD的最大值改为求正n边形ACDEF…（图11）的任一顶点的最大值？探究如下：
如图4，D′是正n边形上任一顶点，求B D′的最大值？设∠ACD′=θ，
，作△BCO，使∠BCO=θ， 
，易得△ACO∽△D′CB， ，AO最大值为BO+1，由此 B D′最大值为
，同时可得最小值为
，其中
。 图4
小结：推广2的问题利用构造两个三角形相似解决。同时在此基础上把试题条件作进一步改变：由“AC上方作一个正n边形ACDEF…”，改为“AC下方作一个正n边形”，D′是正n边形上任一顶点，求B D′的最大值？探究发现最值是一样的，证明方法类似，在此省略。
结束语：本题的条件背景从正三角形变化到正多边形，试题问题从一个点到任意点，解题方法从构造全等到构造相似，都体现了特殊与一般的关系。
客服QQ：30444492琼网文【2021】1550-113号
增值电信业务经营许可证：琼B2-20210322
出版物经营许可证：新出发龙华出字第(2021)009号
广播电视节目制作经营许可证：(琼)字第00779号
版权所有 ©2002-2024 期刊网 琼ICP备2021005105号
