发展课内阅读，深探数学之美

发展课内阅读，深探数学之美

古永贵

广东省东莞市厚街湖景中学 523946

【摘要】 中学生学习能力强，精力充沛，好奇心强，根据他们的学习特点，很有必要拓展数学阅读，以此深探数学之美，提高学生学习数学的兴趣，引领学生树立远大志向，用学到的知识回馈社会。

【关键字】 课内阅读；数学阅读；数学美

1 问题的提出

《初中数学课程标准》中提到情感与态度目标：能积极参与数学学习活动，对数学有好奇心与求知欲。在数学学习活动中获得成功的体验，锻炼克服困难的意志，建立自信心。初步认识数学与人类生活的密切联系及对人类历史发展的作用，体验数学活动充满着探索与创造，感受数学的严谨性以及数学结论的确定性。形成实事求是的态度以及进行质疑和独立思考的习惯。

当代数学教学节奏快，容量大，重复练习多，这样不但没有提高数学学习的效率，反而大量消耗了学生的学习精力，事倍功半。中学生学习能力强，精力充沛，好奇心强，根据他们的学习特点，很有必要发展数学课内阅读，以此深探数学之美，提高学生学习数学的兴趣，引领学生树立远大志向，用学到的知识回馈社会。

2 初中阶段，哪些方面适合开展数学阅读

2.1 学习新的知识模块时，适合开展阅读

数学教学活动必须建立在学生的认知发展水平和已有的知识经验基础之上。如果是一个新的知识模块，在学习新课时学生没有经验可寻，课后就会出现知识混乱。这时，如果教师在教学过程中设置一节跟新知有关的阅读课，让学生弄懂新知的来龙去脉，或理解新知的内涵，加深学生对新知的理解，这样，更有利于学生接受新知。

例1.1 在《实数》的学习中，课本简单提到在进行实数运算时，有理数的运算法则及运算性质等同样适用。但学生在实际的学习中是不理解这句话的内涵的，所以在实数范围内的计算的过关情况就不够理想。教师可以设置一节阅读课《为什么说 不是有理数》，学生通过阅读，了解无理数的起因和发展，知道简单的证明方法，知道无理数是实际存在的不能写成分数形式的数，它和有理数一样，都是现实世界中客观存在的量的反映。

例1.2 在《锐角三角函数》的学习中，通过引进锐角三角函数，建立直角三角形中边角之间的关系。这与前面所学的由边求边，知角求角的知识不同，并且锐角三角函数是用三个学生不熟悉的符号sin，cos，tan联系直角三角形中角与边的关系，学生对这样的符号感到陌生，这种陌生感会直接阻碍学生接收新知识。由此，教师可以在新课学习时设置阅读《一张古老的“三角函数表”》，让学生了解三角函数的产生和发展，帮助学生更好地理解锐角三角函数是一种函数，它建立了锐角与它的边的比之间的对应关系。

2.2 易错点、常考点，适合开展阅读

在数学的学习过程中，有些常规知识，虽然出现的频率很大，但学生总是避免不了要犯错。究其原因，是跟学生没有理解知识的内涵有关。因此，教师可以在易错点教学时设计合理的阅读，使学生充分理解知识的内涵，从而真正掌握知识。

_{例2.1 在学习全等三角形的判定时，我们知道能够判定两个三角形全等的方法有SSS，SAS，ASA，AAS，HL。对于SSA，课本设置了一个思考栏目，用做实验的方式探讨满足两条边和其中一条边的对角分别相等，不能保证两个三角形全等，从而得出SSA不能用来判定两个三角形全等。这个反例很直观，但学生在使用这些方法时，还是会不经判断就选用了这个错误的判定方法。在这里，教师可以设置阅读《为什么SSA不能证明两个三角形全等》，学生通过阅读和动手操作，深刻理解并验证这个判定方法是不可行的，这样，就不会在今后的练习中轻易出错。}

例2.2 如图，已知菱形OABC的边OA在x轴上，点B的坐标为（8,4），点P是对角线OB上的一个动点，点D（0,2）在y轴上，当CP+DP最短时，点P的坐标为_________.

在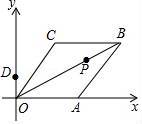 解决这类题目时，我们用到的是“将军饮马”问题中的解题原理，先作C点关于OB对称的点A，再根据“两点之间，线段最短”，连接AD，与对称轴OB的交点就是所要找的点P。为了解析清楚这个原理，教师可以安排阅读“将军饮马”这个故事，并要求学生动手画一画。这样，学生在阅读故事的过程中掌握了一种解题方法，以后遇到这类问题，直接用“将军饮马”来解析即可。

2.3 提升学生的审美观，适合开展阅读

很多人认为，学习数学是枯燥的，只有领悟了数学的真谛的人，才能从心里感受到数学的美。一道道简单的数学算式，一幅幅非凡的几何图形，一个个有趣的智力游戏，蕴含了不一样的数学美。教师应充分挖掘体现数学美的教学资源，精雕细琢，在课堂上让学生体验数学之美。

例3.1 人教版八年级数学上册 的《杨辉三角》

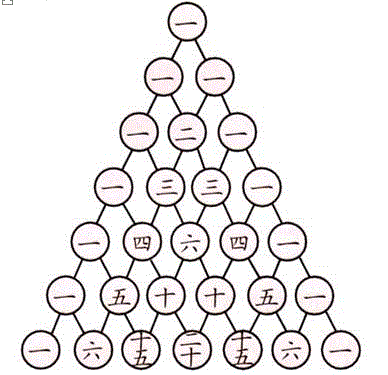
教师在课程设计时，除了安排学生阅读课本上的阅读资料，还可以引导学生查阅资料，深入探究与杨辉三角有关的知识：杨辉的先进教育思想；他在中国数学教育史上的重要地位；与“杨辉三角”相关的“贾宪三角”“帕斯卡三角”。这样，不仅激发了学生的学习兴趣，而且拓宽了学生的视野，为进一步学习数学奠定了基础。

例3.2 游戏“24点”，从简单的“3,3,6,10”，“2,3,3,7”到稍微复杂一点的“5,5,5,1”，“1,3,4,6”，各个年龄段，都能挑战，可谓是老少咸宜的一个游戏。教师在设计这样的游戏课堂时，还可以布置学生课后查找资料，寻求解决游戏的通用方法，引领学生求知索源，吸收更多更广的知识。许多包含数学知识的小游戏，最能激发学生的学习兴趣，激活学生的数学思维。如能在班级定期举行这样的游戏活动，定能大大提高学生学习数学的兴趣。

2.4 引领学生树立远大理想，适合开展阅读

泰戈尔说过：“理想是指引方向的航标灯。”欧几里得，黎曼，笛卡尔，杨辉，华罗庚，陈景润……这些伟大的数学家，就像一盏盏明灯，照亮着天下学子的求知之路。现在的学生，很多都没有明确的学习、生活目标，更谈不上为追求远大理想而努力奋斗。教师可以在教学过程中，适当安排学生阅读一些名人成长的励志故事，在潜移默化中使学生吸取正能量，引领学生树立正确的人生价值观。

3美好愿景

希望通过数学课内阅读课，提高学生学习数学的兴趣，拓宽学生在数学方面的视野，培养学生刻苦专研、求知索源的良好学习习惯。希望通过数学课内阅读课激发学生的学习积极性，向学生提供充分从事数学活动的机会，帮助他们在自主探索和合作交流的过程中真正理解和掌握基本的数学知识与技能、数学思想和方法，获得广泛的数学活动经验。

【参考文献】

［1］中华人民共和国教育部. 义务教育数学课程标准[M]. 北京: 北京师范大学出版社, 2011.

［2］欧几里得著，兰纪正等译. 几何原本. 西安: 陕西科学技术出版社, 1990.

［3］吴文俊主编. 世界著名数学家传记（上册）. 北京: 科学出版社, 1995.

［4］吴文俊主编. 世界著名数学家传记（下册）. 北京: 科学出版社, 1995.