“牛喝水” 衍生的最值问题

“牛喝水” 衍生的最值问题

付丽 蔡正涛

陕西省汉中市 勉县致远中学

陕西省汉中市勉县勉阳初级中学

“牛喝水”问题的实质是轴对称问题，其衍生的最短距离问题是初中阶段典型的几何最值问题。直线、角、三角形、四边形、圆、抛物线等几何图形均可作为这个模型的载体，勾股定理、函数等知识也与它联系紧密，尤其是结合图形变换后，这类问题对学生分析问题、解决问题的能力要求更高。在教学过程中，不能只强调解题技巧，要引导学生剖析问题本质及解题原理，设计分层拓展训练，渗透转化、化归、迁移等数学思想，促使学生在积累解题经验的同时提升认知水平。下面说说教学中遇到的动点最值几种常见题型。

引例 如图，牵牛从点A出发，到河边l喝水，再到点B处吃草，求最短路径。

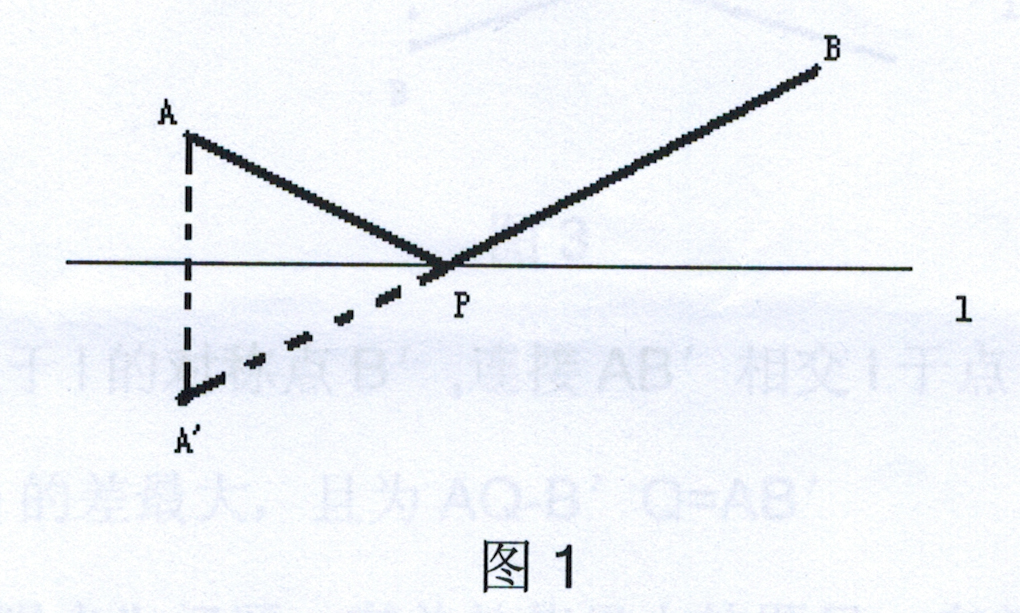
作点A关于l的对称点A＇，连接A′ B，与l的交点P，即牵牛沿AP走到P处喝水，再PB沿到B处吃草，这样走的路径最短，即AP+BP最小。

1. 两定一动型

如图 1 ，在 △ ABC 中， AC = BC = 2 ，∠ACB =90°, D 是BC 的中点， E 是 AB 边上一动点，则 EC + E D的最小值是

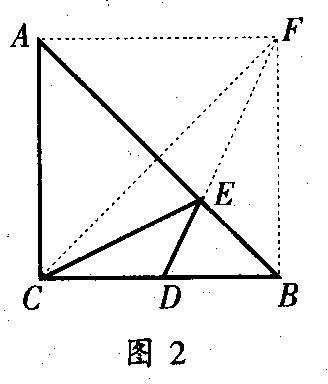图1

解析： C 、D 是两定点， E 图 1 是在直线 AB 上移动的一动点，以 CA 、 CB 为边作正方形 A C BF ，则 C 关于 AB 的对称点一定是 F ，连接 DF 交 AB 于 E ，则这时 EC + ED 最小，因为 D 是 BC 的中点，在直角三角形 FBD 中，则 EC + ED= ED + EF = DF = 。

二、一定两动型

如图2，点P是∠AOB内一定点。分别在OA、OB边上找点M、N，使△PMN的周长最小。

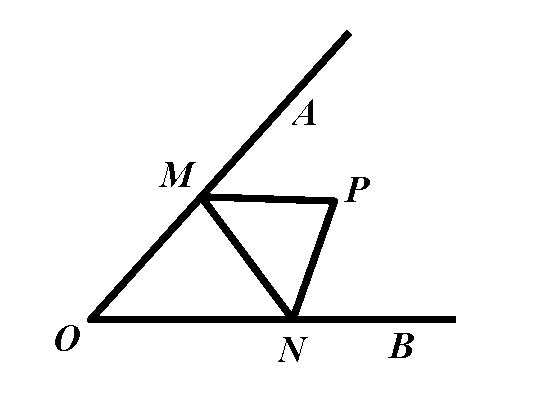
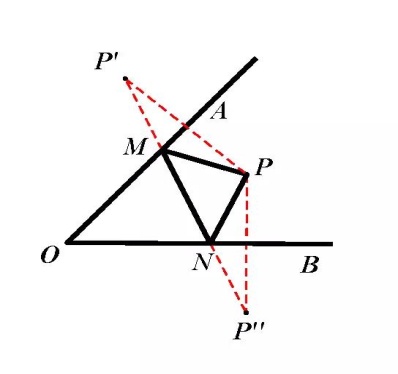图2

解析：△PMN的周长=PM+MN+NP，可以利用作轴对称，把这三条线段转化为同一直线上的线段。如图2，分别作点P关于OA、OB的对称点P＇、P＇＇，连接P＇P＇＇，分别交OA、OB于点M、N，连结PM、PN，此时PM=P＇M，PN=P＇N，

三、两定两动型（两个动点分别在两条直线上）

已知：点P、Q是∠AOB内部两定点，分别在直线OA、OB上找点M、N，使四边形PMNQ的周长最小。

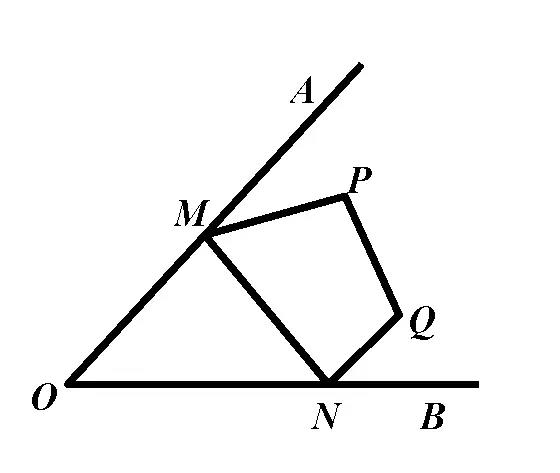
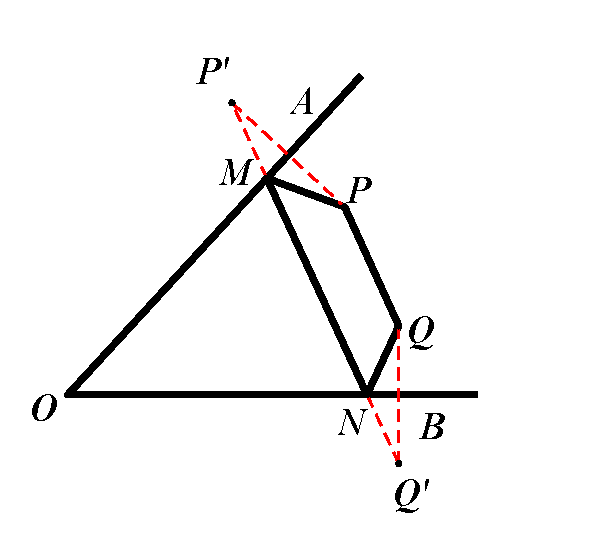图3

解析：因为PQ的长度是定值，要使四边形PMNQ的周长最小，就是要使PM+MN+NQ的值最小。作点P关于OA的对称点P’，作点Q关于OB的对称点Q’，连结P’Q’，分别交直线OA、OB于点M、N，连结PM、MN、NQ，因为PM=P’M，QN=Q’N，所以四边形PMNQ的周长=PM+MN+NQ=P’Q’+PQ，因为PQ是定值，而PM+MN+NQ的最小值为P’Q’的长度，所以此时四边形PMNQ的周长最小。

三、两定两动型（两个动点在一条直线上）

如图4 在平面直角坐标系中，矩形OACB, OA = 3 ,OB=4 , D 为边 OB 的中点。若点 E 、F 为边 OA 上的两个动点，且 EF = 2 ，当四边形CDEF的周长最小时，求点 E 、F 的坐标。

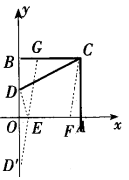图4

解析： 现在要找两个点 E 、F ，使四边形CDEF的周长最小，由于 E 、F 间的距离是定值，通过平移使 F 点与 E 点重合，化两动点为一动点问题，即同时平移 F 、C 使得 F 与E重合， C 平移到 G（平移的距离均为 EF 的长），这时就转化为原型：在 x 轴上找一点 E ，使得 ED +EG的值最小，四边形 CDEF的周长＝DE +CD +CF + EF ，因EG=CF, 而CD 和 EF 的长是定值，所以当 ED + EG的值最小时，四边形CDEF的周长最小。将 C向左平移两个单位得到 G ( 1 , 4 ) ，作D关于 x 轴的对称点D’（ 0 ，- 2 ) ，连结D’G交 x 轴于 E , 由点D’,G的坐标，求得直线 CD’的解析式：y=6x-2,当y=0时，x= ，所以E点为( ，0 ) ，因为 EF=2所以F点为( ，0)

“两定两动一线”型对学生的思维能力，知识迁移能力的要求更高，通常要通过平移，将两动点转化为一动点的问题，这就要求学生深刻领悟，灵活转化。

四、三动型

所谓“三动型”是指三个点均为动点的条件下求最值问题，即直线l同侧有两个动点 A 和 B ，在直线 l 上求一动点P，使 PA + PB 最小。

如图5，菱形ABCD中， AB = 2 ，∠BAD=60°， E 、F 、P 分别是 AB 、BC 、AC 上的动点，求 PE + PF 的最小值。

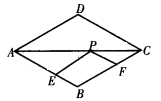
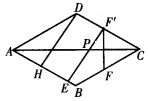图5

解析： 解答本题需要分二步： ① 根据轴对称变换，将 PF 进行转化，确定P点位置； ② 由于 E 、F 为动点，当 EF’ ⊥ AB时，EF’的长度最短，此时EF’的长度为 PE + PF 的最小值。在菱形 ABCD 中，对角线AC平分∠ BCD ，作 FF’ ⊥ AC，即F’、F 关于 AC对称，连接 F’E交 AC 于 P ，当F’E ⊥ AB 时，F’E的长度最小，过点D作 DH ⊥ AB 于 H ，因为 AD = AB =2,∠BAD=60°所以 DH =

，即PE + PF 的最小值为 。本题由于是三个动点，虽然解题思路不变，但是除了按照常规思路确定P点以外，还要确定何时F’E 的最小，即F’ E 为垂线段时值最小。

数学思想引领方法,数学课堂固然应该教会学生更多的数学知识与解题技巧，但更重要的是让学生在学习与应用这些知识与技能的过程中获得数学思想。在解决最短距离问题时，化曲为直是数学转化思想的直观体现,轴对称是常见的解题方法，常用依据为“两点之间线段最短”与“垂线段最短”两大公理。

— 4 —