广东省茂名市第一中学
摘要:基于当前高中教学来看,主要侧重于理论知识学习和试题解答,忽略了学生的生理差异以及学习能力。本文提出的探究式教学法,通过设置情境、有效设问、分组讨论,能够有效完成中数学教学的目标与任务,有利于提高学生的学习热情,促进学生的全面素养发展。
关键词:高中数学;探究式教学;运用
数学作为高中阶段的重要科目,一直以来受到传统教育的束缚。多数学生在数学学习的过程中无法感受数学知识的乐趣,难以与现实的生活进行有效的联系。在新课程标准中,越来越多地强调培养学生的全面素养以及学习方法的重要性。数学知识学习是一个发现问题、解决问题的过程,而探究式教学法通过引导学生对于数学问题展开探讨,有利于提升学生的思维创新能力以及提高学生的学习热情[1]。本文提出将探究式教学法应用到高中数学教学,并结合自己的教学经验提出了建议,希望能为一线的数学教师提供参考。
从理论层面而言,探究式教学法指的是在教学过程中,学生自主参与到问题探索之中,降低学生对于教师的依赖,是处于一种探究式的情境下开展学习活动。学生在这个学习的过程中不仅学习到了知识,同时还发展了数学思维。不仅如此,开展探究式教学法,教师通过将学生分成学习小组,让学生在组内分析数学规律以及推导数学公式,能够进一步提升学生的实践能力以及培养学生的组织协作能力[2]。
如何培养学生的思维能力,问题导入是其中最为有效的环节,因此在探究式教学中注重问题导入环节对于探究式教学的意义十分重大。大部分的数学问题是从生活现象中抽象形成,通过情景教学法还原问题的本来面目有利于提升学生的理解能力。另外教师在设置情境时还需要注重培养学生发现问题、分析问题以及解决问题的能力。例如复数教学,教学情境创建过程如下。教师开场白:16世纪,在意大利有个伟大的数学叫做卡尔达诺,有一天他遇到一个难题:“有两个数,它们的和是10,积为40。”经过推导后他发现这两个数是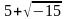 和
和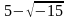 ,这是因为:
,这是因为: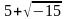 +
+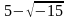 =10,(
=10,(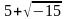 )*(
)*(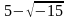 )=40。从上述结果我们可以看出
)=40。从上述结果我们可以看出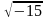 也是一个存在的数,那么
也是一个存在的数,那么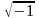 应该也是一个存在的数。后来数学家们将
应该也是一个存在的数。后来数学家们将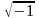 =i,那么
=i,那么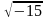 =
=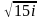 ,由此就引入了一个新数i,通过建立故事的情境增加学生复数学习的兴趣,进一步提出问题:形如▁叫做复数,常用字母▁表示,即复数的代数形式为▁,其中▁叫做复数的实部,▁叫做复数的虚部,全体复数构成的集合叫做▁,常用字母▁表示。教师通过结合数学史的资料进行提问,有利于拓展学生的思维,培养学生的综合素养。
,由此就引入了一个新数i,通过建立故事的情境增加学生复数学习的兴趣,进一步提出问题:形如▁叫做复数,常用字母▁表示,即复数的代数形式为▁,其中▁叫做复数的实部,▁叫做复数的虚部,全体复数构成的集合叫做▁,常用字母▁表示。教师通过结合数学史的资料进行提问,有利于拓展学生的思维,培养学生的综合素养。
当学生形成了问题意识,此时教师应当引导学生对于问题进行猜想。任何伟大的发现都是基于猜想的基础上而展开,对于高中生而言,猜想不仅是一种学习方法,更是创造性思维的体现。因此在探究式教学中猜想可分为以下三步:首先引导学生观察与发现,通过已经学习的数学知识来思考问题的关键;其次教师需要引导学生进行总结和归纳相应的数学规律;最后引导学生对于数学问题展开合理假设大胆猜想并尝试进行验证。
例1:在线段[0,a]上随机地投三个点,试求由点O至三个点的线段能构成一个三角形的概率。”
设事件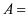 “三线段能构成一个三角形”,设三线段长分别为
“三线段能构成一个三角形”,设三线段长分别为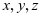 ,则
,则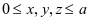 ,
,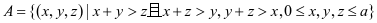
则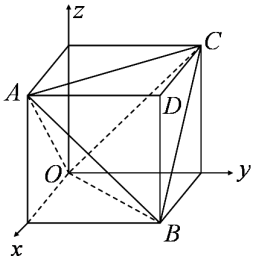 总事件几何区域是
总事件几何区域是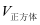 ,事件
,事件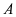 的几何区域是
的几何区域是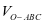
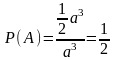
这种方法的难点在于如何将事件的几何区域描述出来。有一些学习程度好的学生提出“有没有简易一些的办法?”因此在教学过程本人引导学生进行思考:这里涉及到三个变量,是“三维”的,因而将其转化为体积比求概率。在本人的启发下学生提出数学中的‘降维’思想。然后学生他们尝试了 “二维”、“一维”的方法,将其转化为面积比、长度比求解,并进行了验证总结。在探索验证的过程中,解题能力得到了提高,同时也培养了学生的思维创新性。
在探究式教学中教师必须要引导学生的思维上升为理性思维,促使学生的数学思维更加深刻。而在数学领域中推导求证是理性思维的重要体现,也是探究式教学的关键。在高中数学中对命题的推理和论证是高中数学教学的重要内容,不仅需要学生具备严谨的思维,同时还需要学生具备一定知识应用能力。从而使得证明推导的过程有逻辑性和条理性。例如在《直线与平面平行的判定》的定理运用,问题探究环节“想一想”中。
(1)判断下列命题的真假?说明理由:
①如果一条直线不在平面内,则这条直线就与平面平行
②过直线外一点可以作无数个平面与这条直线平行
③一直线上有二个点到平面的距离相等,则这条直线与平面平行
(2)若直线a与平面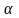 内无数条直线平行,则a与
内无数条直线平行,则a与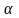 的位置关系是:A、a ||
的位置关系是:A、a ||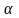 B、a
B、a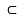
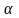 C、a ||
C、a ||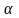 或a
或a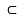
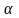 D、
D、
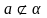
上述题目中①②大多数同学能运用定理判断出真假,但③部分学生存在疑问。因此教师进行引导提问:不在平面内的一条直线与平面的位置关系有哪些?请你们作出相应的图形。
在这个过程中,本人通过引导学生对自己的推理过程进行反思,同时引导学生通过数形结合思想来证明的自己的观点,从而培养学生思维的深刻性。
综上所述,探究式教学通过建立起问题情境,吸引学生的注意力,鼓励学生对数学问题猜想,引导学生进行推理论证,有利于深化高中数学课堂的教学内容。同时希望广大的高中数学教师能够深入探索探究式教学的内容,并建立共享平台促进探究式教学的推广。
参考文献
袁国颖.浅析高中数学教育中探究性教学[J].高中数理化, 2019(2).
向克民.论探究式教学在高中数学教学中的应用策略[J].数学学习与研究:教研版, 2019(10):13-13.
刘调芳.谈职业高中数学探究式教学方法[J].内蒙古教育, 2019(12).
王丽君.问题探究 活跃课堂——论高中数学探究式教学模式[J].科技资讯, 2020, v.18;No.585(12):131-132.