河堤极限承载力的有限元分析研究

河堤极限承载力的有限元分析研究

赖耀平

深圳市宝安排水有限公司 广东省深圳市 518000

摘要：水资源承载力是指某个区域的特定时段内支撑经济社会发展并能保障生态系统正常运转的水资源系统最大规模，它是一个反映该区域水资源是否能够承载该地区经济社会发展的重要评价指标，对研究区的水资源承载力的评价、区域水资源的合理利用以及地区经济的健康发展有着重要的作用。

关键词:有限元方法；极限承载比；阈值优化；计算误差；河道堤防

引言

环境容量是在特定时空内有效可交换水体的同化能力，以及在规定环境目标下所能容纳污染物的量。换言之，排入海域污染物浓度不超过环境管理标准的前提下所能允许的最大排放量，是海洋环境容纳污染物的最大容量[1]。河口海域水体污染物成分往往是人为因素影响在自然本底值上的加合，这种加合超过一定限度时，就会改变环境质量。因此，环境容量是环境质量评价、环境监测和环境承载力预警的基础，也是河口海域资源开发利用的环境依据。关于环境容量的研究，目前国内外学者已进行了很多工作，海域环境容量的研究也越来越受到重视。

1研究方法

将有限元和传统弹性模量方法进行耦合对其承载比进行计算

式中:ηe，i为承载比极限值;Se，i为有限元计算相同时效的堤防承载力，kPa;Se，0为不同有限计算单元的承载比极限值，其中Se，i的计算方程为:

式中:σ为不同计算有限元的应力值，kPa;σs为强度折减系数。在进行承载比极限值计算基础上，对其均匀度进行计算:

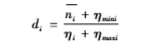
式中:d为承载比极限值对应的均匀度;ηi为有限计算单元平均承载比;ηmax，i和ηmin，i分别为有限计算单元的承载比最大和最小值;ηmax，i和ηmin，i的计算方程分别为:

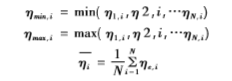
式中:N为有限计算单元的总个数。有限元分析方法对各计算单元的承载比阈值进行优化计算:

式中:η0，i为堤防承载比的标准值。对承载比阈值优化后的弹性模量能量和耗能方程分别进行调整:

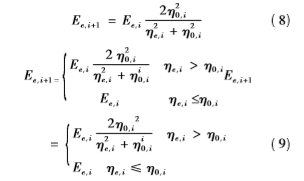
式中:Ee，i+1、Ee，i分别为第i个和第i+1个计算有限单元的静力荷载，kPa。对上述两个方程进行有限元迭代求解计算:

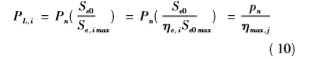
式中:PL，i为模型求解的河道堤防的极限承载力，kPa;Pn为荷载基准值。

2模型应用

2.1水质模型

鉴于本文研究的海域为近岸浅水区，表层和底层物理、化学和生物性质差别较小，水平方向和垂直方向上的变化可忽略[15]，因此采用深度平均。二维流体动力学方程和水质控制模型方程如下：

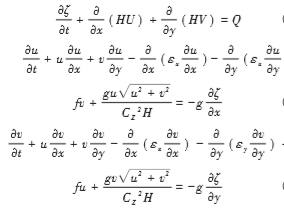
式中：ζ为平均海平面以上的瞬时水位高度，单位：m；H为水深，单位：m；Q为径流量；g为重力加速度，单位：m/s2；U和V分别为垂直平均流速在x和y轴上的分量，单位：m/s；f为柯氏参数，f=2ωsinφ，ω为地转角速度，φ为地理纬度；C为谢才系数，C=1nH16；n为曼宁系数（取0.025～0.035）；t为时间；x和y平面取在未扰动的平均海平面上，z轴垂直向上，构成右手坐标系（见图1）。式（1）—（3）的初始条件从静止水状态开始，U=V=ζ=0。边界条件分两类：沿岸闭边界，取法向流速等于零（Vn=0）；开边界各点水位为时间的已知函数，即ζ=ζ(t)。

2.2计算步骤及加载方式

运用ABAQUS中自带的Geostatic分析步进行模型初始地应力场平衡，平衡过程中“杀死”桩单元；提取地应力数据作为模型的初始地应力场，同时“激活”桩单元及桩土接触面，进入荷载分析步对桩顶施加水平荷载。桩顶水平荷载采用单向分级的方式进行施加，依据《建筑基桩检测技术规范》[13]中对单桩水平静载试验的要求：单向分级加载时，分级荷载不应大于水平极限荷载或最大试验荷载的1/10，当桩顶水平位移超过30~40mm时终止加载。本次模拟计算中，通过预估最大与最小加载量，设置分级加载大小为60kN，当桩顶水平变形超过40mm时，终止加载。

3极限承载力试验结果

对于河道堤防极限承载力的测定试验主要通过螺旋桩抗拔进行测定，当螺旋桩顶部位移以及荷载变化点达到最高点位时，河道堤防处于极限承载状态。从河道极限承载力试验测定结果可看出，当1#螺旋桩的钻孔深度达到4.16m时，其极限位移处于最高点为1.55m，极限承载力为75.99KN，2#螺旋桩的钻孔深度达到4.61m时，其极限位移处于最高点为1.65m，其极限承载力测定值为80.33KN，从各螺旋桩的极限承载力测定结果可看出，钻孔深度对其顶部位移和荷载变化影响相对较小，判定的河道堤防的极限承载力只和其顶部位移具有较为直接的联系。3#和4#螺旋桩钻孔深度均高于5.0m，其相比于1#和2#螺旋桩，较容易出现失稳现象，其极限承载力也要小于1#和2#螺旋桩的极限承载力。河道堤防计算的极限承载比和试验测定的极限承载比的总体误差要低于15%，误差产生的原因主要为堤防基准面和实际基准面之间存在一定的差异，使得计算的极限承载比和实际测定的承载比存在一定的误差。

3.1基于入湖河流生态环境流量需求下的流域水环境承载力

通过外流域补水多口分流和本区多水源工程（包括上游水库下泄、河道区间汇流、提标尾水回用等）的优化配置，不仅可为湖周入湖河流的生态环境用水提供良好的水源保障，同时亦可改善草、外海的水动力条件，让更多的清洁水量从水质相对较好的外海东岸入湖，并经外海北部的水体置换通道和海口河排出，从而可有效提升滇池水环境容量（见图6）并促进滇池草外海水质持续性改善。在入湖河流生态环境流量保障方案下，扣除湖面降雨降尘、内源释放及湖面蒸发浓缩挤占的环境容量后，滇池流域3指标（TP、TN、CODMn）可利用的水环境容量分别为125.3t/a、2961t/a、6661t/a，分别较入湖河流环境流量无保障方案增加了4.4%、5.0%、8.6%，其中草海各指标的水环境容量增幅很大（分别为23.5%、14.7%、32.3%）；外海尽管分流了部分水量进入草海，但随着入湖水量的空间优化，其水环境容量仍较分流入草海前有所增加，外海3指标的容量亦分别增加1.7%、3.7%、5.5%。基于入湖河流生态环境流量需求下的入湖水量及过程的空间优化调整，可较大程度地提高滇池流域的水环境承载力，可为滇池流域产业结构调整、空间管控规划、流域总量控制预留一定的安全余量及全面推进河湖长制和流域水环境质量持续性改善提供科学的技术支持。

3.2塔墩承载能力评估

１）结构强度检算。该塔墩塔柱及横梁为钢筋混凝土结构，受力形式为偏心受压构件，在基本组合下塔墩纵向最大轴压力为４３　８８３ｋＮ，对应的弯矩为４２６　００１ｋＮ·ｍ。考虑损伤后塔墩底部矩形截面偏心受压的正截面设计轴力为６５５　７９７ｋＮ，设计弯矩为２　７１８　８２１ｋＮ·ｍ，基于偏心距及结构重要性系数，正截面轴力效应值为４６８　６０１ｋＮ，弯矩效应值为１　９２３　４８３ｋＮ·ｍ，损伤后的正截面设计值均大于正截面效应值，说明考虑结构损伤后塔墩正截面强度仍满足规范要求。２）塔墩变形检算。根据原设计规范，在汽车荷载（不计冲击力）作用下塔墩变形限值ｆＬ＝Ｚ１Ｌ（已考虑承载能力检算系数）。依据计算模型，塔墩在汽车荷载作用下的最大变形为７５ｍｍ＜４３７ｍｍ（桥塔高度为１１８．２ｍ），故塔墩变形仍满足规范要求。３）裂缝宽度验算。根据原设计规范，在正常使用极限状态下，塔墩裂缝为０．１３６ｍｍ＜０．２５×１．１１ｍｍ＝０．２７８ｍｍ，故塔墩裂缝仍满足规范要求。

3.3生态承载力

尽管国内外学者对生态承载力进行了很多研究，但生态系统的复杂性使得生态承载力的内涵至今没有较为统一的界定。有的学者认为，生态承载力是一个包括自然、经济、社会环境等内容的综合评价指标；也有学者认为，生态承载力应该更突出生态系统在提供物质供给和废物吸纳方面的承载力。第一类观点虽然能够全面评价生态承载力，但因包含多方面评价因素，对承载力的“生态性”体现不够充分。生态承载力集中体现了系统对自然界物质的承载能力，同时因旅游服务的特殊性还要兼顾考虑游客感知体验的承载力。因此，生态承载力是指在不降低系统废弃物吸纳能力和动植物群落恢复能力前提下，确保不降低游客旅行体验的最大游客数。生态承载力受海岛自身资源和生态环境状态所限，是自然界的一种客观存在。海岛生态系统脆弱、生态修复难度大，在开展旅游业的过程中更应严格保护脆弱的海岛生态环境，不突破生态承载力底线。

3.43障碍度分析

为了甄别黄河流域九省水资源承载力障碍因素，根据障碍度模型，对其障碍因素进行分析。如图5所示，研究期内，水资源子系统平均障碍度11.55%，远高于社会经济子系统的5.67%和生态环境子系统的6.60%，说明水资源子系统对于水资源承载力的影响巨大，是提升区域水资源承载力的更重要的障碍因子。从各年平均障碍度来看，在水资源子系统中，水资源量和年均降水量是主要的障碍因子，多年平均障碍度分别为24.73%和14.02%；在社会经济子系统中，耕地灌溉率和人均GDP是主要障碍因子，多年平均障碍度分别为11.65%和10.01%；生态环境子系统中，生态环境用水率和森林覆盖率是主要障碍因子，多年平均障碍度为13.94%和4.62%。从各指标上看，人均水资源量、年均降水量、生态用水率、耕地灌溉率和人均GDP是障碍因子平均障碍度排序前五的指标，其中排名前两名的均为水资源子系统，说明水资源子系统是限制水资源承载力水平提升的最为重要的指标层。从时间层面来看，这五个指标在2008至2017年间的每一年都排名前五，只是每一年障碍度排序略有变化，说明限制水资源承载力水平提升的主要障碍因子均无太大变化。

3.5经济承载力

有学者结合旅游产业评价了经济承载力水平。认为旅游经济承载力是指在不损害生态环境和游客体验的条件下，当地经济对旅游产业发展的可接受水平。测度可接受水平的方法包括单指标和综合评价两种。常见的单指标有经济规模、特定区域承载人数等，综合评价是从人口、资源、社会、生态、基础设施等多方面构建综合指标体系。上述两种测算方法默认经济承载力是个固化的概念，未充分体现在生态承载力刚性约束下发展旅游经济的最大能动性

结束语

旋桩顶部位移和荷载变化点达到最高点时，水流坝处于极限荷载状态。河流坝计算极限荷载比与试验确定的极限荷载比之间的总误差小于15%，主要原因是大坝库与实际库之间存在一定差异，导致计算极限荷载比与实际月荷载比之间存在一定误差2)有限元法通过离散计算单位调整和优化负荷率参数阈值，从而加快了模型解决方案的收敛程度，使其计算误差优于传统弹性模量计算方法。

参考文献

[1]刘建梅,谢丽莉,刘宇.广东省雷州半岛水资源承载能力分析[J].广东水利水电,2019(11):47-51+55.

[2]孙桂英.改进弹性补偿有限元法的堤防承载力计算——以赣江南昌段为例[J].黑龙江水利科技,2019,47(10):114-116+147.

[3]赵元秀.重力式挡土墙加高方式探讨[J].江淮水利科技,2019(04):8-9.

[4]李铁林.泉州后渚油库码头部分塌陷原因探讨[J].福建交通科技,2019(03):135-136.

[5]何光景.本溪市水资源承载力评价[J].黑龙江水利科技,2019,47(02):9-12.

[6]潘奇兵.加强城市治理增强承载能力[J].城乡建设,2019(04):48-50.

[7]李树森,李想,魏美竹,刘世轩,李树.对通辽市科左后旗马莲河关地窝堡段河道地质条件的探讨[J].内蒙古水利,2019(01):70-72.