浅谈连接体问题动力分配原理

浅谈连接体问题动力分配原理

冯鹏元1

新疆克拉玛依市高级中学，新疆 克拉玛依 834000

摘要：通过一般性模型的分析，推导了在水平面、斜面和竖直面上做匀加速直线运动的连接体物体之间相互作用力与恒定外力的定量关系。得到的一般性结论，从多个方面对连接体问题做了拓展和延伸，有助于深入理解连接体问题相互作用力的分析。

关键词：连接体；匀加速直线运动；牛顿第二定律；动力分配；等效动力

连接体是指物体之间通过轻绳、轻弹簧相连接或者直接接触而构成，此模型是一个相互联系、相互制约的体系^[1]，对于在恒定外力作用下做匀加速直线运动的连接体问题，特别是在求相互作用力时，一般方法是先用整体法求加速度，再用隔离法求相互作用力^[2]。从常规方法出发，相互作用力的大小与恒定外力和物体质量之间遵循一定的规律，我们称之为动力分配原理。利用动力分配原理可以快速地解决连接体中物体间的相互作用力的问题，还可对各种情形的连接体问题进行分析探究，通过推导和归纳结论，由此来拓展思路，提高解题效率。

1 模型中原理的证明

有这样一种模型，质量为m₁和m₂的物体用平行于斜面的轻绳、轻弹簧和直接接触的方式相连接（图1），放在倾角为θ的粗糙斜面上，斜面的动摩擦因数为μ，在m₁上施加一 平行于斜面向上的恒力F ，使两物块沿斜面向上做匀加速直线运动，求m₁和m₂之间的相互作用力满足的表达式。

图1 基本模型

证明：对m₁和m₂（包括轻绳、轻弹簧）整体分析

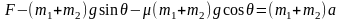
对m₂隔离分析（轻绳、轻弹簧和直接接触的相互作用力统一用N表示）

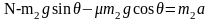
由以上两式联立得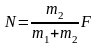

注：也可以通过如下方法证明，当物体系统同时受到几个力的作用时，应用质点系的牛顿第二定律可得^[3]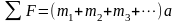

对于单个物体应用牛顿第二定律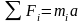

可得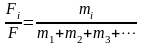

即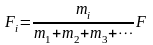

说明：（1）条件：连接体系统中，两(多) 物体相对静止一起运动，具有相同的加速度；各物体接触面粗糙程度相同；力与运动方向在一条直线上。

（2）分类：①μ= 0， 即斜面光滑；② θ= 0，即在水平面上；θ= 90。即在竖直面内；③a= 0 即匀速直线运动。

（3）影响因素：m₁和m₂之间的相互作用力与接触面是否光滑无关，与物体是在水平面、在斜面还是在竖直面内运动无关^[4]。

结论：动力分配原理：两个物体（系统的两部分）在外力（总动力）的作用下以共同的加速度运动时，单个物体（系统的一部分）分得的动力（两物体之间的相互作用力）与自身的质量成正比，与系统的总质量成反比，而该动力即为两物体间绳子拉力、轻弹簧弹力、接触面弹力等。

2 特殊模型原理的拓展

情景1，如图 2所示，两个外力（动力）作用在m₁和m₂两个物体上，在动摩擦因数为μ的水平面上做直线运动，这两个力水平且方向相反，试分析在运动过程中两物块之间的弹力多大。

图2 双侧受力

分析：假设F₂>F₁，

整体分析：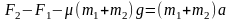

隔离m₂分析：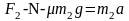

由以上两式联立得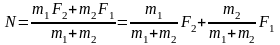

小结：(1) 若F₂与F₁ 方向相反，两物体接触面的作用力为F₂与F₁独立作用时，所提供的动力代数之和，发现叠加后有加强的效果。

(2) 若 F₂与F₁ 方向相同，同理可得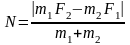 ，发现叠加后有减弱的效果。

情景2， 如图3（a）、（b）所示，质量分别为m₁和m₂的物体之间用轻绳连接，在m₁上施加一斜向上的拉力F或者斜向下的推力F，二者一起做匀加速运动，设物体与水平面之间的动摩擦因数为μ，分析轻绳的张力。

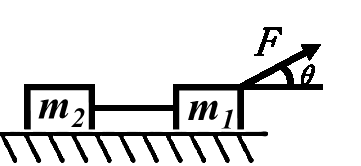
图3（a）、（b）倾斜动力

分析：在图3（a）中，

整体分析：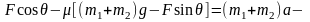

隔离m₂分析：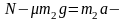

由以上两式联立得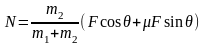

同理可得：在图3（b）中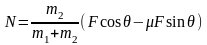

小结：在图3（a）情景中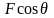， 是系统外力F在运动方向上的分力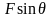， 是系统外力F在垂直于运动方向的分力，竖直向上，使摩擦力减小，则动力增加了 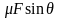，所以我们将 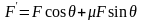称为等效动力^[5]，表示动力在运动方向上产生的作用效果。在图3（b）情景中，外力F在垂直于运动方向的分力，竖直向下，使摩擦力增大，则动力减小了 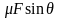，即等效动力为 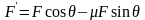，也表示动力在运动方向上产生的作用效果。

情景3，如图4所示，质量为m₁和m₂的物体叠放在一起，放在倾角为θ的粗糙斜面上，斜面的动摩擦因数为μ，在m₁上施加一平行于斜面向上的恒力F ，使两物块沿斜面向上做匀加速直线运动，分析两物体之间的相互作用力。

图4 叠放模型

分析：整体分析：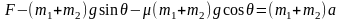

隔离m₂分析：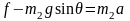

由以上两式联立得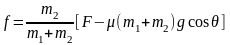

小结：此情景中，系统除外力F外，还受到斜面的滑动摩擦力，此时滑动摩擦力为阻力，则动力减小了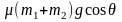 ，所以等效动力为 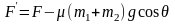，表示动力在运动方向上产生的作用效果。

3 动力分配原理的复杂应用

如图5所示，木块A、B静止叠放在光滑水平面上，A的质量为m，B的质量2m．现施加水平力F拉B，A、B刚好不发生相对滑动而一起沿水平面运动；若改用水平力F´拉A，要使A、B不发生相对滑动，F＇的最大值。

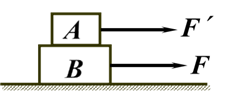
图5

分析：水平力F拉B时

A、B刚好不发生相对滑动，A、B之间的静摩擦力为最大静摩擦力f_m，应用动力分配原理

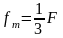
水平力F´拉A时

A、B不发生相对滑动，A、B之间为静摩擦力f，应用动力分配原理

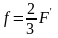
又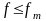

所以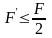

如图6所示，质量为m₁、m₂、m₃的木块以线a、b相连，质量为Δm小木块置于中间木块上，施加水平力F拉m₃而使系统一起沿水平面运动；若将小木块从中间木块移至质量为m₃的木块之上，两细绳上的张力T_a、T_b的大小，以及如何变化。

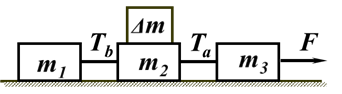
图6

分析：质量为Δm小木块置于中间木块时：

对m₁、m₂、Δm整体分析，应用动力分配原理

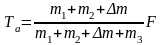
对m₁分析，应用动力分配原理

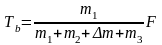
质量为Δm小木块置于最右边木块时：

对m₁、m₂整体分析，应用动力分配原理

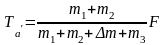
对m₁分析，应用动力分配原理

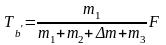
所以，

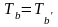
如图7所示，在光滑水平面上放置质量分别为m和M的四个木块，其中两个质量为m的木块间用一不可伸长的轻绳相连，木块间的动摩擦因数为μ，最大静摩擦力大小等于滑动摩擦力，现用水平拉力F拉其中一个质量为M的木块，使四个木块以同一加速度运动，则轻绳对m的最大拉力。

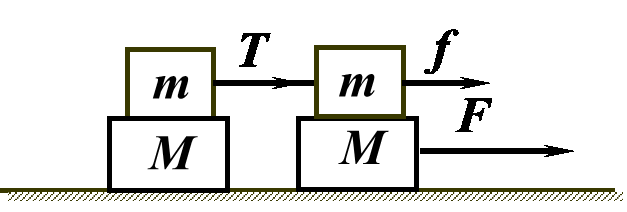
图7

分析：对左边m和M整体分析，应用动力分配原理

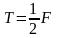
即F最大时，拉力T最大，要使四个木块以同一加速度运动，即m和M要相对静止。拉力最大时，m和M之间的静摩擦力为最大静摩擦力μmg，应用动力分配原理

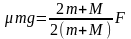
所以，当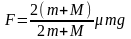 时，绳子拉力最大

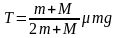
通过以上典型模型的分析，我们可以看出动力分配原理在解决连接体问题的优越性，但是在应用过程中，必须要满足动力分配原理的适用条件，特别是作用于整体的等效动力的确定尤为重要，这样才能准确的应用动力分配原理，提高学习效率和解题的速度。值得一提的是，动力分配原理作为高中物理中一个很重要的二级结论，它可以完美的解决多变、灵活和复杂的连接体问题，比如：可解决双体和多体运动问题，平面、竖直和斜面运动问题，单侧、双侧和多侧受力问题，平行和倾斜动力问题，都遵循动力与质量成正比的分配 规律，为我们教学和学生解决问题多提供了一种可能性。

参考文献

[1]郑金．用动力分配法巧解匀加速运动连接体问题[J]．中学物理教学参考，2015，44(7)：9-11．

[2]刘伯渊．“连接体问题”的一般解法[J]．物理教学探讨，2007，25(19)：37-38．

[3]沈晨，徐承楠．更高更妙的物理[M]．浙江：浙江大学出版社，2012：30-31．

[4]金嵩洲，吴宇峰．浅析连接体的动力分配原理[J]．中学物理，2013，31 (23)：34-35．

[5]傅新锦，陈明媚．运用结论速解一类连接体问题[J]．中学物理，2008，26(12)：39-40．

1作者简介：冯鹏元（1991-），男，中学一级教师，主要从事高中物理教学工作，曾获第35和37届全国中学生物理竞赛优秀指导老师。