新疆生产建设兵团
摘 要:本文由一元二次方程式的求根公式判别式,推导出一个数学方程式。作为充分大奇数的奇合数与奇素数的判别式。
关键词:奇合数、奇素数、判别式
在自然正整数Z—集合里,对任意大的奇数:m,如何判断它是“奇合数”或“奇素数”,至今未有定型的数学表达式来判定。
(A)
奇合数的因数分解
一、基本概念:
1、充分大奇合数概念:
在自然正整数Z—集合里,充分大奇数设定为:m。即 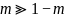 。
。
2、充分大奇合数概念:
设定:两个充分大的不同等的奇数为p和q。
若: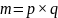
则:m为奇合数,p与q是m的两个因数。
3、充分大奇合数的表达式:
将m变形为 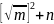
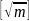 为最大整数部分
为最大整数部分
n为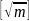 的余数部分
的余数部分
令: 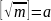
得: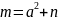
由: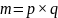
令: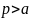 ,则
,则 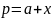
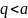 ,则
,则 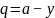
得: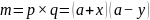
即: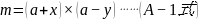
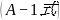 是m的数学表达式。
是m的数学表达式。
二、求解数学方程式: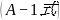
1、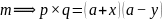
将: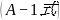 演算化简:
演算化简:
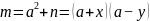
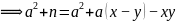
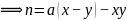
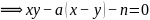
设: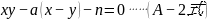
在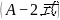 中:令
中:令 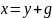 ,g为
,g为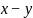 的差,即
的差,即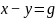
将: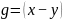 ,代入
,代入 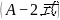 中
中
得: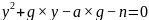
用:求根公式
得: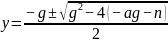
在上式中:a与x及y互为奇偶数, x-与y同为奇偶数。
可将分母2约去。
得: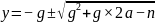
要使y有正整数的解值
数式: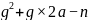 ,必须是完全平方数式方程。
,必须是完全平方数式方程。
令: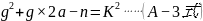
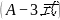 就是推导出的任意奇合数m的因数分解方程式。
就是推导出的任意奇合数m的因数分解方程式。
诠释: 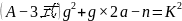
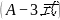 是本文研讨的主题方程式。
是本文研讨的主题方程式。
在此式中:a,n是工作目标任意选定的m。
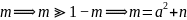 视为常量(已知量)。
视为常量(已知量)。
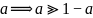 a的数值大小确定工作目标的长度。
a的数值大小确定工作目标的长度。
g及K为未知量(自变量),由a的数值确定它的取值域。是可数的数域。
用阶数表示m的数位。
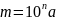 其中:a =1,2,3……9
其中:a =1,2,3……9
n=1,2,3……(可以无限)
当n=6或5时: 用于演算较为容易。
用于演算较为容易。
当n=7,8,9……16时: 用于演算较为困难。
用于演算较为困难。
当n=17,18,19……任意大时: 时,非手工能演算,得用科技设备来完成。
时,非手工能演算,得用科技设备来完成。
本文范例,选择15>n的工作长度。
即 15位数以内的奇数数值。
2、根据完全平方数的数值特征:
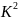 被 16整除的余数设为
被 16整除的余数设为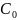
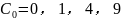 有4个数值特征。
有4个数值特征。
以16为模,将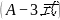 构建为同余式方程:
构建为同余式方程:
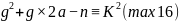
g 被16整除的余数为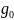 ,即
,即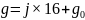
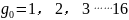 有16个余数
有16个余数
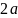 被16整除的余数为
被16整除的余数为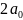 ,即
,即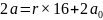
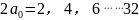 有16个余数
有16个余数
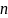 被16整除的余数为
被16整除的余数为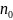 ,即
,即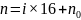
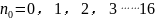 有17个余数
有17个余数
将 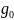 ,
,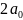 ,
,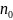 ,进行三、三组合
,进行三、三组合
取得: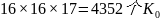 数值。
数值。
在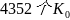 数值中,被16整除,余数为0,1,4,9的
数值中,被16整除,余数为0,1,4,9的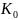 有989个,其余
有989个,其余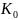 舍去。
舍去。
这989个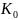 与对应的
与对应的 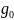 ,
,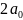 ,
,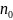 构建成数学方程式:
构建成数学方程式:
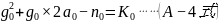
令名为:“初始数值方程式”: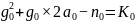
在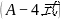 中:
中:
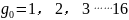
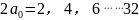
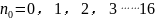
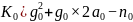 是
是 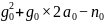 的运算数值。
的运算数值。
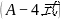 为
为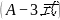 的“初始数值方程式”。
的“初始数值方程式”。
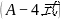 :
: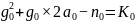 的数值演算表太冗长,在本文中略去。
的数值演算表太冗长,在本文中略去。
3、奇合数因数分解实例
取充分大奇合数 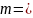 631697288726223
631697288726223
①m变形为: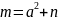
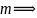 631697288726223
631697288726223
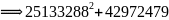
②求出: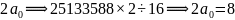
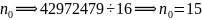
③ 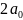 ,
,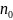 与
与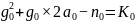 初始数值演算表中的
初始数值演算表中的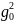 、
、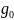 、
、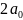 、
、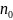 行列对应的数值表中,行列对应的数值有1—4列存在。可拓展为1—4个“工作目标m的求解方程式”
行列对应的数值表中,行列对应的数值有1—4列存在。可拓展为1—4个“工作目标m的求解方程式”
工作目标初始值数学方程式数值演算表
①+②×③=④-⑤=⑥
① | ② | ③ | ④ | ⑤ -n | ⑥ | |||
| | | | 0 | -1 | -2……-15 | -16 | |
| | | | | | | | |
144 | 12 | 8 | 240 | | | -15 | | 225 |
| | | | | | | | |
注:此实例:行列对应的数值表中,只有一列,即可拓展1个求解方程式。 | ||||||||
4、拓展:
将 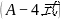 :
: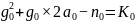
拓展为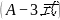 :
:
将: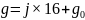 、
、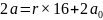 、
、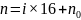 代入
代入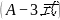
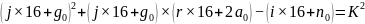
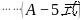
将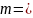 631697288726223
631697288726223 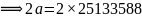
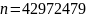
代入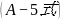 中:
中:
得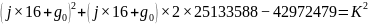
上式就是“工作目标m的求解方程式”
在此方程式中,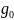 的数值为12。有未知量 j与K:
的数值为12。有未知量 j与K:
K为此方程式的演算数值是因变量。
j为此方程的自变量,可为大于1的任意自然数1,2,3……,是有限的可数的自变量。
j的取值域是:
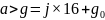 (
(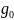 可以忽略不计)
可以忽略不计)

得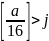 ,是工作目标的长度j,它的取值次数是小于
,是工作目标的长度j,它的取值次数是小于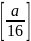 。如果用逐一取值求解,最大工作长度是
。如果用逐一取值求解,最大工作长度是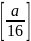 次,即
次,即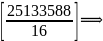 1570849次
1570849次
用手工演算,是相当困难的。如果工作目标m的数位在8位以内是比较容易的。
为缩短的j的取值次数,用16的方幂法确定j的取值区间,即g数值区间。
5、用16的方幂法确定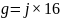 的取值区间
的取值区间
| 释表 | ||
1×160 ∽ 1×16 | 1 ∽ 16 | 1
16 | j的取值域是在
手工运算,j的取值约在 163—165之间。(4096—108576) 在16n—16n+1之间 插入 可以组合成16n—16n+1之间 任意自然数R:16n<R<16n+1 |
1×161 2×161 ∽ 16×161 | 1×161 2×161=32 ∽ 162=256 | 161
162 | |
1×16×16 2×16×16 ∽ 16×16×16 | 162=256 2×162=512 ∽ 163=4096 | 162
163 | |
1×163 2×163 ∽ 16×163 | 163=4096 164=65536 | 163
164 | |
1×164 2×164 ∽ 16×164 | 164=65536 165=1048576 | 164
165 | |
1×165 2×165 ∽ 16×165 | 165=1048576 166=16777216 | 165
166 | |
16×165 ∽ 16×166 | 166=16777216 167=268435456 | 166
167 | |
|
|
| |
| 16n ∽ | 16n | |
6. g的取值数域表
160—166数值列表
1-16 平方数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
160—161 | 1×160 1 | 2×160 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
161—162 | 1×161 =16 | 2×161 =32 | 48 | 64 | 72 | 96 | 112 | 128 | 144 | 160 | 176 | 192 | 208 | 224 | 240 | 256 |
162—163 | 256 | 512 | 678 | 1024 | 1280 | 1536 | 1792 | 2048 | 2304 | 2560 | 2816 | 3072 | 3328 | 3584 | 3840 | 4096 |
163—164 | 4096 | 8192 | 12288 | 16384 | 20480 | 24576 | 28672 | 32768 | 36864 | 40960 | 45056 | 49152 | 53248 | 57344 | 61440 | 65536 |
164—165 | 65536 | 131072 | 196608 | 262144 | 327680 | 393216 | 458752 | 524288 | 589824 | 655360 | 720896 | 786432 | 851968 | 917504 | 983040 | 1048576 |
165—166 | 1048576 | 2097152 | 3145728 | 4194304 | 5242880 | 6291456 | 7340032 | 8388608 | 9437184 | 10485760 | 11534336 | 12582912 | 13631488 | 14680064 | 15728640 | 16777216 |
(可扩值为:16n-1—16n)根据工作的数位,选择工作目标的数域。
7、工作目标: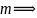 631697288726223
631697288726223
 测值求解演算表
测值求解演算表
序号 | ① | ② | ③ | ④ | ⑤ | | 注: | ||
g的测试数式 | 1×164 | 2×164 | 3×164 | -4×162 | | | 根据工作目标长度g的测试,数值域选择在4位数与6位数之间,测值求解的g初始值选择为164=4096 | ||
g的测试数值 | 4096 | 8192 | 12288 | 11264 | -4 | | |||
① | ① | | 16777216 | 75300864 | 150994944 | 126877696 | 126787600 | | |
② | +② | | 4096 | 8192 | 12288 | 11264 | 11260 | | |
③ | ×③ | | 50267176 | 50267176 | 50267176 | 50267176 | 50267176 | | |
④ | -④ | -n=42972479 | -42972479 | -42972479 | -42972479 | -42972479 | -42972479 | | |
⑤ | =⑤ | 非K2数值 | 205868157633 | 411821034177 | 617791881153 | 566293375681 | | | |
⑥ | ⑥ | K2数值 | | | | | 566092216881 | | |
| |||||||||
注:经 测值求解演算表的推演:
测值求解演算表的推演:
求得解值: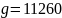
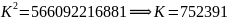
将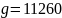
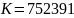 代入
代入 中:
中:
得: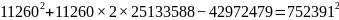
 方程得解。
方程得解。
8、解值效验:
由设置:
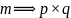
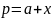
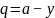
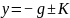
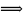 代入
代入 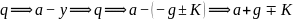
现经“ 解值测试演算表”
解值测试演算表”
求得解值 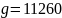
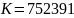 代入
代入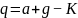
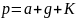 得:
得: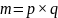
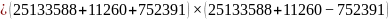
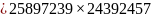
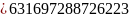
解值效验正确,工作目标完成,因数分解成功。
奇合数因数分解,以分解成两个奇数乘积为目的。
9、工作目标 范例:奇合数设为m
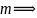 67543109679101
67543109679101 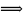 82184612+8470580
82184612+8470580

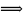
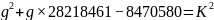
经  测试求解值演算表(A表)和(B表)
测试求解值演算表(A表)和(B表)
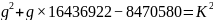
获得共同解值: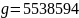
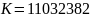
解值效验: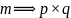
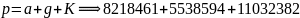
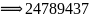
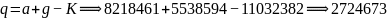
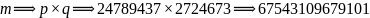
工作目标、范例:  ①+②=③ ③+④=⑤ ⑤+⑥=⑦
①+②=③ ③+④=⑤ ⑤+⑥=⑦
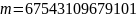 测试求解值演算表(A表)
测试求解值演算表(A表)
序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ||
测试数式 | 5×165 | 4×164 | 8×163 | 3×162 | 2×161 | | | ||
测试数值 | 5242880 | 262144 | 32768 | 768 | 32 | 2 | | ||
① | ① | | 27487790694400 | 30305289240576 | 30667140235264 | 30675646873600 | 30676001342464 | 30676023496836 | 30676023496836 |
② | +② | | 5242880 | 5505024 | 5537792 | 5538560 | 5538592 | 5538594 | 5538594 |
③ | ×③ | | 16436922 | 16436922 | 16436922 | 16436922 | 16436922 | 16436922 | 16436922 |
④ | -④ | -n | -8470580 | -8470580 | -8470580 | -8470580 | -8470580 | -8470580 | -8470580 |
⑤ | =⑤ | 非K2数值 | 113664591839180 | 120790930866124 | 121691386920908 | 121712517115360 | 121713397565728 | 121713452593924 | |
⑥ | ⑥ | K2数值 | | | | | | | 121713452593924 |
测试演算求得解值: | |||||||||
( | |||||||||
工作目标、范例  ①-②=③ ③-④=⑤ ⑤-⑥=⑦
①-②=③ ③-④=⑤ ⑤-⑥=⑦
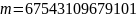 测试求解值演算表(B表)
测试求解值演算表(B表)
序号 | ① | ② | ③ | ④ | ⑤ | ⑥ | ⑦ | ||
测试数式 | 6×165 | -11×164 | -7×163 | -12×162 | -13×161 | | | ||
测试数值 | 6291456 | -720896 | -28672 | -3072 | -208 | -14 | 5538594 | ||
① | ① | | 39582418599936 | 31031138713600 | 30712522604544 | 30678482681856 | 30676178577664 | 30676023496836 | 30676023496836 |
② | +② | | 6291456 | 5570560 | 5541888 | 5538816 | 5538608 | 5538594 | 5538594 |
③ | ×③ | | 16436922 | 16436922 | 16436922 | 16436922 | 16436922 | 16436922 | 16436922 |
④ | -④ | -n | -8470580 | -8470580 | -8470580 | -8470580 | -8470580 | -8470580 | -8470580 |
⑤ | =⑤ | 非K2数值 | 142994581667788 | 122593990459340 | 121804094922700 | 121719560775628 | 121713837791660 | 121713452593924 | |
⑥ | ⑥ | K2数值 | | | | | | | 121713452593924 |
| |||||||||
注:①测试演算求得解值: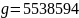
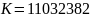
②  测试求解值演算表(A表)和(B表):
测试求解值演算表(A表)和(B表):
(A表)是从较小取值,逐步增值演算求解。(B表)是较大取值,逐步减值演算求解。
还可以先增后减,或先减后增演算求解。
(B)
奇素数的判别式及求证方法
在Z—正整数集合中,充分大的奇数: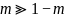 或为奇合数,或为奇素数,二者必居其一,非此即彼。
或为奇合数,或为奇素数,二者必居其一,非此即彼。
本文在研讨(A)时,奇合数的判别式是: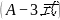

此式只有一个唯一的正整数解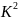 是完全平方数式方程式。
是完全平方数式方程式。
此式的其它解值是非完全平方数解值(含多个分数式或无理数式解值),这就是奇素数。
即是:  有解,则
有解,则 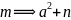 为奇合数
为奇合数
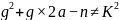 无解,则
无解,则 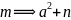 为奇素数。
为奇素数。
如何判别充分大的奇数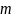 为素数:
为素数:
将把要工作的m,按照(A)的变形方法
构建形如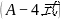 :
:
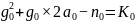
按照(A)奇合数因数分解实例:
将 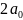 、
、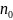 与
与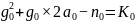 初始数值演算表中的
初始数值演算表中的 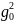 、
、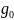 、
、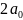 、
、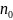 行列对应的数值演算表中
行列对应的数值演算表中
将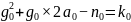 拓展为:
拓展为:
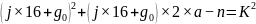 因数分解方程式
因数分解方程式
上式就是“工作目标 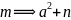 的求解方程式”
的求解方程式”
在此方程式,a 与 n 是已知量,j 与 K 是未知量。j 为方程式的自变量。它的定义域为: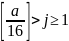 。
。
K为方程的演算数值。按(A)的求解方法,就是奇素数的求证方法。它只有非完全平方数解值,这就是它的判别式。
诠释:充分大的奇合数与奇素数的判别式,为同一个数学方程式:

它的解值为:完全平方数(正整数)是“奇合数”。
它的解值为:非完全平方数(分数或无理数)是“奇素数”。
这是本文研讨的主题。
作者:新疆生产建设兵团 王述勋 2021.6.18
参考文献:
① 王述勋. 充分大奇合数因数分解方程式推介.“试题与研究”. 教学论坛. 2020(26):0113-0115.
② 王述勋. 完全平方数及完全平方数式方程式浅析. “教学与研究”. 教育研究 201-204.
(C)
附录:(A—3式) 的应用
的应用
在数域较小的正整数Z—106集合里,将集合里的奇数,设为:m(6位数或小于6位数),进行“奇合数因数分解”及“奇素数素性判别”的手工操作方法——是本文(A—3式)  的应用
的应用
操作流程实例
实例(一):设6位数的奇数 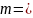 732843
732843
(1)将m变形为: 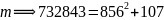
即: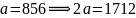

代入(A—3式) 式中
式中
得: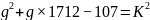
列表演算: 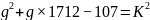 的数值。
的数值。
(2)  数值演算表
数值演算表
①+②×③-④=⑤=⑥
① | ② | ③ | ④ | ⑤ | ⑥ |
| | | | 非 | |
1 | 1 | 1712 | -107 | 1016 | |
4 | 2 | 3424 | -107 | 3321 | |
9 | 3 | 5136 | -107 | 5038 | |
16 | 4 | 6848 | -107 | 6757 | |
25 | 5 | 8560 | -107 | 8478 | |
36 | 6 | 10272 | -107 | | 10201 |
(3)释表:
①g可以逐一取值:1,2,3……
g的取值域为: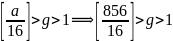
②g在逐一取值演算中,取得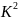 数值,对应的
数值,对应的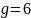 就是奇合数m的解值。
就是奇合数m的解值。
此实例 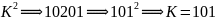
③将取得的解值效验:(A)的设定:
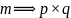
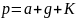
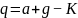
此实例中
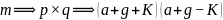
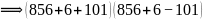
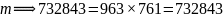
(4)诠释:按此操作,证得奇数 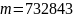 为“奇合数”。
为“奇合数”。
实例(二):设5位数的奇数 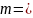 30031
30031
(1)按实例(一)的工作操作方法
得: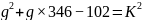
列表演算: 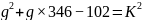 的数值。
的数值。
(2)  数值演算表
数值演算表
①+②×③-④=⑤=⑥
① | ② | ③ | ④ | ⑤ | ⑥ |
| | | | 非 | |
1 | 1 | 346 | -102 | 245 | |
4 | 2 | 692 | -102 | 594 | |
9 | 3 | 1038 | -102 | 945 | |
16 | 4 | 1384 | -102 | 1298 | |
25 | 5 | 1730 | -102 | 1653 | |
36 | 6 | 2076 | -102 | 2010 | |
49 | 7 | 2422 | -102 | 2369 | |
64 | 8 | 2768 | -102 | 2730 | |
81 | 9 | 3114 | -102 | 3093 | |
100 | 10 | 3460 | -102 | 3458 | |
| | | | | |
终止演算 | |||||
(3)释表:
①g的取值到最大数值: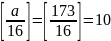
无取得 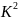 数值。g取大值,未有
数值。g取大值,未有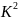 数值。
数值。
与g值对应,“终止演算”
即 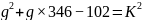 无解。
无解。
② 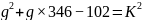 方程式无解,
方程式无解,
即可判别 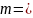 30031 为“奇素数”。
30031 为“奇素数”。
(4)诠释:较小数位(6位或5位)的奇数,是可以用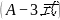 的求值演算,来判别其是“奇合数”或“奇素数”的判别方法。
的求值演算,来判别其是“奇合数”或“奇素数”的判别方法。
结束语:此手工演算方法,进行“奇合数因数分解”及“奇素数素性判别”,适用于广大的数论“爱好者”。
8