(海装广州局驻昆明地区第三军事代表室 , 云南 昆明 )
摘 要: 分别利用匹配滤波算法与短时傅里叶算法对测距脉冲及其回波进行时延检算,对比二者在窄脉冲(低功耗)条件下的仿真结果,针对测距脉冲“跨周期”现象,采取不同中心频率下正调频脉冲—负调频脉冲交替发射的方式,仿真结果验证了该探测方式的有效性。
关键词: 避碰声呐; 时延估计; 匹配滤波
1 前言
避碰声呐一般安装于水下自主航行器的头部,为其提供前方有无障碍物及障碍物距离信息。避碰声呐通过主动发射脉冲、检测回波信号时延对障碍目标完成距离估计,在产品低功耗要求下,探测脉冲的脉宽受到限制,短时傅里叶算法的时延估计性能随脉宽的减小迅速下降。本文基于匹配滤波算法,通过包络提取和正负调频信号交替发射,提高了避碰声呐在窄脉宽条件下的测距精度,解决了测距脉冲的跨周期问题。
2 两种时延估计算法
2.1 短时傅里叶
短时傅里叶算法的基本思想是用窗函数来截取信号,它是一种线性变换,满足叠加原理,概念明确,是目前研究非平稳信号应用最为广泛的一种方法[1]。设信号为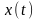 ,分析窗为
,分析窗为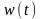 ,可定义
,可定义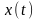 的短时傅里叶变换为:
的短时傅里叶变换为:
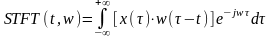 (1)
(1)
时间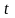 处的短时傅里叶变换的计算过程如下:
处的短时傅里叶变换的计算过程如下:
将窗函数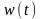 由时间零点处平移至时间
由时间零点处平移至时间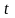 处,得到
处,得到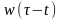 ;
;
信号被平移后的分析窗加窗隔断后,得到短时信号:
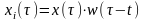 (2)
(2)
利用傅里叶变换得到短时信号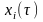 的频谱。
的频谱。
设分析窗的持续时间为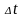 ,则加窗截断相当于取
,则加窗截断相当于取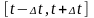 范围内的非平稳信号进行傅里叶变换。若期望时间分辨率高,则分析窗的持续时间必须尽量短。
范围内的非平稳信号进行傅里叶变换。若期望时间分辨率高,则分析窗的持续时间必须尽量短。
2.2 匹配滤波
匹配滤波器是白噪声背景下有规信号检测的最佳接收机[2]。设接收机的输入是确知的有限能量信号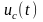 (其复数形式为
(其复数形式为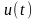 ),接收系统响应函数是
),接收系统响应函数是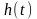 ,传递函数是
,传递函数是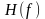 ,在
,在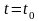 时的输出是:
时的输出是:
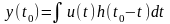 (3)
(3)
或 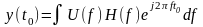 (4)
(4)
使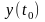 达到最大值的系统定义为与信号
达到最大值的系统定义为与信号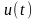 匹配的匹配滤波器系统简称匹配滤波器。
匹配的匹配滤波器系统简称匹配滤波器。
由Schwartz不等式
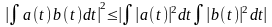 (5)
(5)
可以确定式(4)最大的条件为:
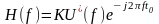 (6)
(6)
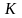 是任一常数,通常取1,相应的响应函数是
是任一常数,通常取1,相应的响应函数是
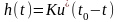 (7)
(7)
匹配滤波器的基本特性如下[3]:
(1)响应函数是被匹配信号的延迟共轭镜像波形;
(2)匹配滤波器相当于一个能计算互相关函数的互相关器;
(3)匹配滤波器对延迟了的匹配信号也是匹配的,只是最大值出现时间向延迟方向平移了一个同样的量。
3 两种时延估计方法仿真对比
相对于短时傅里叶测距算法,匹配滤波算法的优势主要体现在窄脉宽(低功耗)条件下测距结果的抗干扰能力,下面分别在不同探测脉宽、不同信噪比下对二者的测距结果进行仿真分析,归一化仿真条件见表1。
表1 时延估计方法仿真参数
参数 | 短时傅里叶测距算法 | 匹配滤波测距算法 | ||||||
信号形式 | 200kHz单频信号 | 中心频率200kHz、带宽20kHz chirp信号 | ||||||
采样频率(kHz) | 500 | 500 | ||||||
目标距离(m) | 75 | 75 | ||||||
脉宽(ms) | 5 | 2 | 5 | 2 | ||||
信噪比(dB) | 0 | -10 | -16 | 0 | -10 | -16 | ||
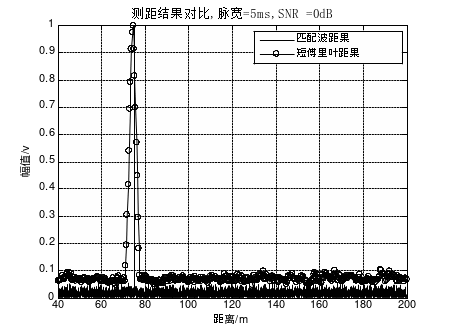
图1 脉宽=5ms,SNR=0dB时两种算法测距结果对比
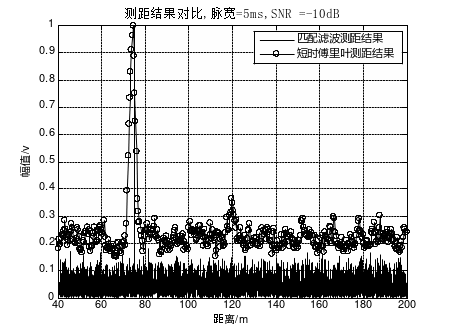
图2 脉宽=5ms,SNR=-10dB时两种算法测距结果对比
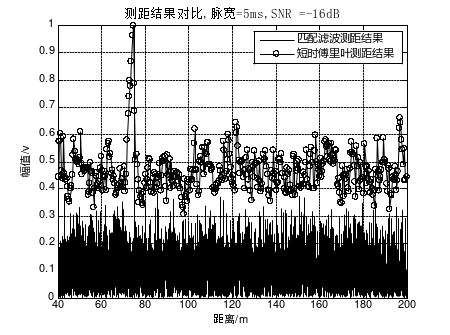
图3 脉宽=5ms,SNR=-16dB时两种算法测距结果对比
当探测脉冲为5ms、信噪比为0dB时,两种算法的测距结果均较为理想,在目标距离75m处形成较为明显的峰值,峰值相对背景有约20dB的增益空间,门限值设置易于把握;对比图1、图2及图3可以看出,随着信噪比降低,两种算法的测距性能呈现出不同程度的下降,但对于距离检算效果影响不大。
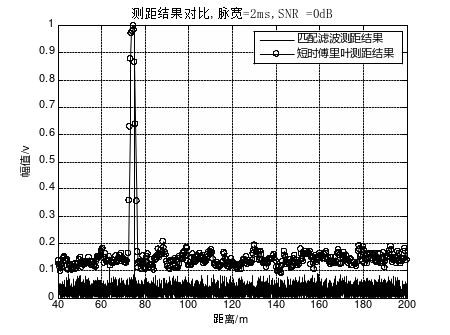
图4 脉宽=2ms,SNR=0dB时两种算法测距结果对比
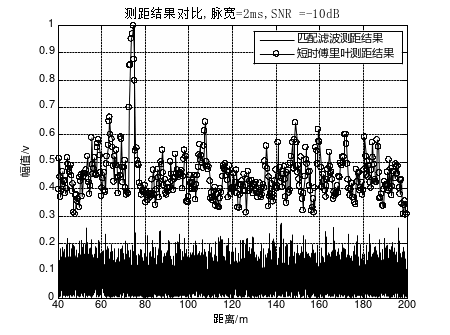
图5 脉宽=2ms,SNR=-10dB时两种算法测距结果对比
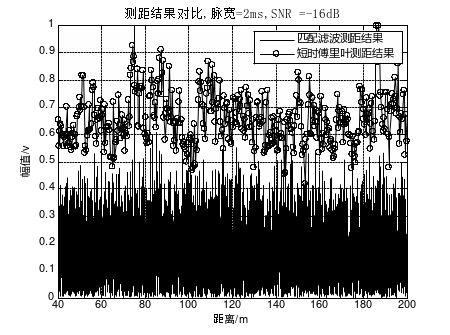
图6 脉宽=2ms,SNR=-16dB时两种算法测距结果对比
图4、图5、图6为探测脉宽2ms时各信噪比下的测距结果仿真。对比图4和图1可知,脉宽变窄对两种算法的抗干扰能力均有一定影响,但在0dB信噪比下基于以上两种算法仍可得到较为准确的目标距离;对比图2和图5,当信噪比下降至-10dB时,短时傅里叶算法对2ms探测脉宽的计算结果出现伪峰,对于门限设定要求十分苛刻,而匹配滤波算法在不同探测脉宽下的测距结果相差不大,其抗干扰能力明显优于短时傅里叶算法;当信噪比下降至-16dB时,短时傅里叶算法在2ms探测脉宽下已无法实现对于目标距离的准确估计,峰值出现在190m左右,而匹配滤波算法依然有6dB左右的门限冗余空间,只要探测门限设置恰当依然可以准确得出障碍目标距离。
4 “跨周期”现象抑制效果仿真
“跨周期”是主动声呐在探测目标过程中较为常见的误判现象[4,5,6]。当探测距离大于脉冲发射周期与介质声速乘积的一半时,回波脉冲与相对应的发射脉冲不在一个探测周期内,由此产生的距离计算失准即为“跨周期”现象。避碰声呐正常探测过程中的发射脉冲和回波脉冲序列如图7所示。
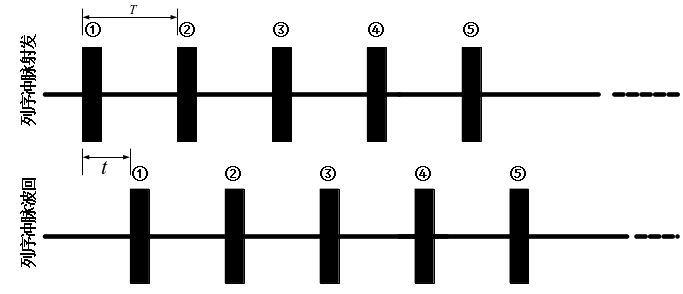 图7 避碰声呐正常探测时发射脉冲及回波脉冲示意图
图7 避碰声呐正常探测时发射脉冲及回波脉冲示意图
图中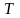 为探测周期,
为探测周期,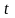 为回波延时,因此可得目标距离
为回波延时,因此可得目标距离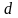 为:
为:
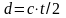 (8)
(8)
式(7)中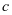 为水中声速。当避碰声呐出现“跨周期”现象时,其发射脉冲和回波脉冲序列如图8所示。
为水中声速。当避碰声呐出现“跨周期”现象时,其发射脉冲和回波脉冲序列如图8所示。
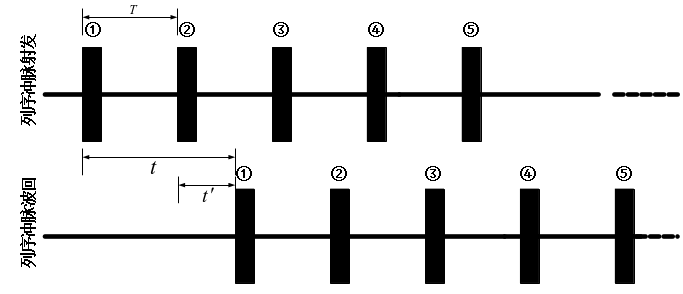 图8 避碰声呐“跨周期”探测时发射脉冲及回波脉冲示意图
图8 避碰声呐“跨周期”探测时发射脉冲及回波脉冲示意图
当探测距离大于脉冲发射周期与介质声速乘积的一半时,回波脉冲将会落入下一个探测周期内,如图8中的1号脉冲回波在2号脉冲的探测周期内,2号脉冲在3号脉冲的探测周期内并以此类推。上图中的真实距离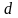 与式(8)定义相同,而探测距离
与式(8)定义相同,而探测距离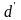 为:
为:
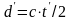 (9)
(9)
由此导致探测距离比实际距离要大,探测误差为一个探测周期的半声程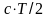 。以匹配滤波算法为例,若相邻两脉冲的频率、相位等信号形式相同,那么必然会出现回波脉冲“跨周期”现象;相反,邻近探测脉冲若采用不同中心频率探测,且将调频方式分为正、负调频,“跨周期”现象将得到有效改善。
。以匹配滤波算法为例,若相邻两脉冲的频率、相位等信号形式相同,那么必然会出现回波脉冲“跨周期”现象;相反,邻近探测脉冲若采用不同中心频率探测,且将调频方式分为正、负调频,“跨周期”现象将得到有效改善。
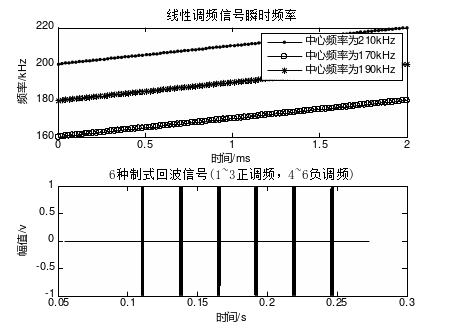
图9 避碰声呐探测脉冲信号形式及回波分布
图9为模拟避碰声呐的探测脉冲,其中1-3号脉冲是中心频率分别为210kHz、170kHz、190kHz的正调频信号,4-6号脉冲是中心频率为210kHz、170kHz、190kHz的负调频信号,分别以1号、4号探测脉冲的信号形式作为基准信号对各回波信号进行匹配滤波,所得结果见图10.
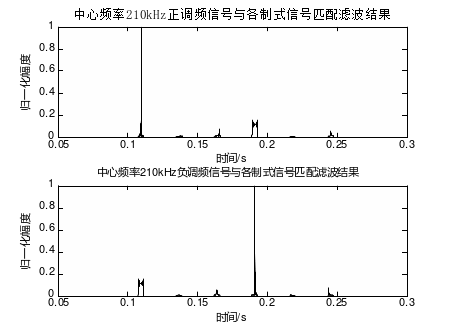
图10 中心频率210kHz的正负调频信号与各脉冲的匹配滤波结果
从图10中可以看出,匹配滤波算法对不同中心频率回波信号的抑制效果较好,相应脉冲与相邻干扰脉冲的匹配结果相差在10倍以上,中心频率相同、调频形式不同的脉冲信号虽然匹配结果相对大一些,然而与相应脉冲的匹配结果相比仍有5倍左右的差距,因此只要判别门限设置得当,“跨周期”现象即可通过该方法得到有效解决。
5 结束语
通过仿真结果可知,相比于短时傅里叶算法,匹配滤波算法的时延估计精度对回波信噪比要求不高,尤其是在低功耗-窄脉冲的探测要求下,匹配滤波算法优势体现的更加明显。针对避碰声呐探测过程中的“跨周期”现象,采取不同中心频率信号结合正负调频的手段,将探测信号分为6种并交替发射,通过匹配滤波算法仿真验证了该探测方式的有效性。
[1] 石海泉.波导环境下矢量声场特性分析及特征提取技术[D],哈尔滨:哈尔滨工程大学出版社,2013.
[2] 鞠德航,林可祥.信号检测理论导论[M],北京:科学出版社,1975.
[3] 朱埜.主动声呐检测信息原理[M],北京:科学出版社,2014.
[4] 侯自强,李贵斌.声呐信号处理-原理和设备[M],北京:海洋出版社,1986.
[5] 李启虎.进入21世纪的声呐技术[D],信号处理,2012.
[6] 孙超,刘雄厚.MIMO声纳:概念与技术特点探讨[D],声学技术,2012.
作者简介:黄凡(1987-),男,工学博士,工程师,主要从事目标特性及辨识技术研究工作。