湖北 应城一中 432400
一、“人船模型”
如
图所示，设人、船的质量分别为
，任一时刻人与船速度大小分别为
，作用前都静止。不考虑水的粘滞阻力，人和船组成的系统在水平方向不受外力，系统在水平方向动量守恒，则 
①
人进船退，人停船停，人由船头走向船尾的这个过程中，始终满足①式，则全过程有：
②
又 
③
由②③得： 
二、“人船模型”的变形
1.“两人一船”型：
例
1.一长为
，质量为
的船上两端分别站有甲、乙两人，质量分别
为和
．当两人交换位置后，船移动距离多大？（其中
）
解：（方法一）先作出如右草图，解法同“人船模型”：
①
②
③
④
由②③④得， 
（方法二）等效法：把（
）等效为一个人，把（
）看成船，用“人船模型”的结论，即得到： 。
在此题中，无论甲、乙谁先走还是同时走，无论在运动过程中谁的速度大谁的速度小，也无论谁先到达船的另一头，最终的结果，船移动的方向和距离都是唯一确定的。
2.“多人一船”型：
例2.小车静置在光滑水平面上，站在车上的人练习打靶，靶装在车上的另一端。已知车、人、枪和靶的总质量为 （不含子弹），每颗子弹质量为
，共
发。打靶时，每发子弹打入靶中，就留在靶里，且待前一发打入靶中后，再打下一发。若枪口到靶的距离为
，待打完 发子弹后，小车移动的距离为多少？
解：等效为“船模型”总质量为
的子弹，运动到小车的另一端，则小车移动的距离可直接由“人船模型”结论得到： 
。
3.“竖直人船”型：
例3.如图所示，质量为 的气球下挂着长为 的绳梯，一质量为 的人站在绳梯的下端，人和气球静止在空中，现人从绳梯的下端往上爬到顶端时，人和气球相对于地面移动的距离？
解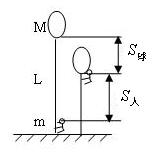
：由于开始人和气球组成的系统静止在空中，竖直方向系统所受外力之和为零，即系统竖直方向系统总动量守恒。得：
解得：
4.“倾斜人船”型：
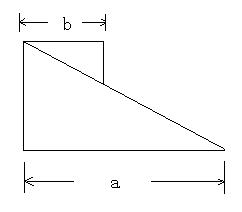
例4.如图所示，在光滑水平地面上，有两个光滑的直角三形木块
和
，底边长分别为
，质量分别为
，若
，且不计任何摩擦力，当 滑到底部时， 向后移了多少距离？
解：选定木块 和 整体作为研究对象，在 沿斜面下滑的过程中，与“人船模型”类同，该系统在水平方向上所受的合外力为零，所以，在水平方向上动量守恒。
设当 沿斜面从顶端滑到底部时， 向后移动了
，则 对地移动了
,由水平方向动量守恒得：
解得：
又：
总之，“人船模型”类问题中，相互作用的两个物体，原来都处于静止状态，相互作用开始后，在整个运动过程中要么动量守恒，要么在某一方向上动量守恒，故称为“人船模型”，它满足“人走船退，人停船止”的规律。处理这类问题时，首先要判断是否符合模型条件，即原来都静止，两物体组成系统要满足动量守恒，解题的关键是画出草图，确定位移关系，根据系统动量守恒，列出方程，解出要求的问题。
客服QQ：30444492琼网文【2021】1550-113号
增值电信业务经营许可证：琼B2-20210322
出版物经营许可证：新出发龙华出字第(2021)009号
广播电视节目制作经营许可证：(琼)字第00779号
版权所有 ©2002-2024 期刊网 琼ICP备2021005105号
