基于均线对上证指数上涨天数的整理和ARIMA模型分析

基于均线对上证指数上涨天数的整理和 ARIMA模型分析

徐亮

山西财经大学 财政与公共经济学院 030000

摘要：确定均线价格作为这次的研究对象，用5、10日均线对上证指数价格先做初步的处理以确定价格涨跌的情况，得出上涨天数的分布情况。针对证券市场频繁出现的上涨趋势，为了发现上涨过程中的拐点，研究对象一段范围的时间序列变量进行模型预测分析。最终发现，ARIMA模型预测工具对前一种方法具有较强的辅助作用，建立的模型能够及时发现上涨过程中的拐点。

关键词：上证指数、样本自相关函数、ARIMA

1 引言

MA均线价格具有追踪趋势、稳定、助涨助跌、支撑线和压力线的特性，所以选取MA均线价格作为我们的研究对象。但是MA均线价格同时也具有的滞后性，在具体运用过程中，也应该纳入考虑范围。证券市场的影响因素有很多，我们将无法对选取的研究对象准确性做出正确的判断，但是这些因素最终都会对价格产生影响。所以我们假设市场价格已经包含一切影响因素。

综合MA均线的各种特性，葛兰维尔（Granvile）提出了“移动平均线八大买卖法则”，我们在此以四大买进时机之一的黄金交叉为理论基础，因为选取的数据时间范围较大，所以利用python对上证指数的上涨天数分布进行整理。但是MA均线固有滞后特性，为了对已形成黄金交叉上涨趋势的股市现象做出及时反应，所以建立ARIMA模型以便及时发现上涨过程中的拐点。

2 研究方法和数据说明

因为数据涉及的时间范围长，数据量比较大，所以选用Python工具对数据进行归纳整理。具体过程：以葛兰维尔移动均线投资法则为基础，对MA5和MA10进行比较，MA5大于MA10的时间点标号为1，反之为0，然后不同时间段连续出现的1进行分段汇总，以此确定连续上涨的天数。在此基础上，对分时段汇总的数据进行进一步归类处理，相同上涨时间天数出现的次数进行汇总。通过汇总的结论，我们可以了解到相同上涨时天数的出现次数。

3实证分析

3.1 单位根检验

为了建立ARIMA模型，首先对变量的平稳性进行检验。Series1为2016年10月11日至12月1日收盘价的三日移动平均值， ∆Series1是对Series1中的数值进行一阶差分处理；Series2为2017年6月1日至8月1日收盘价的三日移动平均值，∆Series2是对Series2中的数值进行一阶差分处理；Series3为2017年6月1日至11月14日收盘价的三日移动平均值，∆Series3是对Series3中的数值进行一阶差分处理。

表1 变量∆Series1、∆Series2、∆Series3平稳性检验

由上图的平稳性检验可知，原时间序列变量都没有通过平稳性检验，所有时间序列变量都是一阶单整，所以建立模型的数据选取变量的差分值。由于模型中的数据都是原变量的差分值，后期依据模型得到的未来几期预测值也是差分值，实际应用过程中，需要原序列的最后一期值和预测期的几期差分值对差分变量进行还原。

3.2 ACF、PACF函数图像选取模型

图1是∆Series1的ACF和PACF图，初步确定ACF图1阶后拖尾、PACF图3阶后拖尾或者ACF图1阶后拖尾、PACF图1阶后拖尾。由于ACF和PACF图有时不能呈现很直观的态势，只能做出大体主观性判断，初步判断ARIMA(1,1,1)和ARIMA(3,1,1)可能性大一点，模型中p和q阶数的确定我们可以根据信息准则进行选择。我们可以得到这两个模型的AIC和SC值，其中ARIMA(1,1,1)的AIC值为2.930，SC值为3.155；ARIMA(3,1,1) 的AIC值为2.919，SC值为3.051，通过AIC和SC信息准则的比较，最终发现ARIMA(3,1,1)模型的AIC和SC值均为最小。又经后期图1和2白噪声自相关检验和正态性诊断，ARIMA(3,1,1)最适合。

图1 2016.10.11-12.01 ACF和PACF图和残差项的ACF图

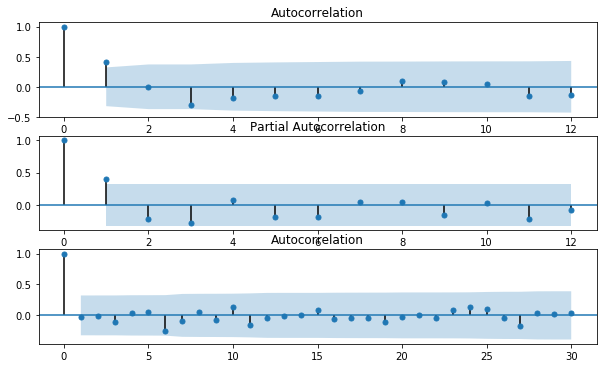
图2 2016.10.11-12.01 ACF和PACF图和残差项的ACF图

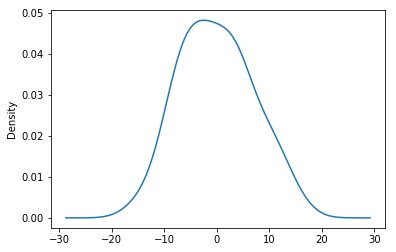
图3是对选取ARIMA(1,1,1)后对模型残差项的正态性诊断。模型选取正确的话，建立模型所得的残差应该服从正态分布。通过对图3.2和图3.3进行比较，图2中的图像形状更加拟合正态分布，最终确定ARIMA(3,1,1)模型。

图3 2016.10.11-12.01年ARIMA(1,1,1)残差项的正态性诊断

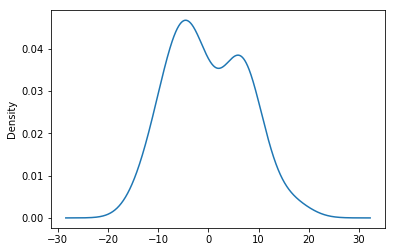
综上所述判断，模型选取ARIMA（3，1，1）。同理，根据∆Series2、∆Series3的ACF和PACF图进行模型的选取和残差项的ACF图和正态性诊断进行模型效果评价确定。按照上面的过程可以得到序列Series2、Series3的模型分别选取ARIMA(5,1,1)和ARIMA(3,1,1)。

3.3数据预测

根据上面所得的式（1）、（2）、（3）对下三期的差分变量值进行预测，因为建立模型的原始变量都是变量的差分值，所以所得的变量值都是未来的三期预测的差分变量值。但是在应用过程中，我们更加关注研究对象的水平值。图4是从2016年10月11日至2016年12月01日水平值以及未来三期的预测值（水平预测值通过差分变量进行还原得到的），具体过程如下：

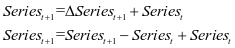
图4 2016.10.11-12.01 ARIMA(1,1,1)模型预测

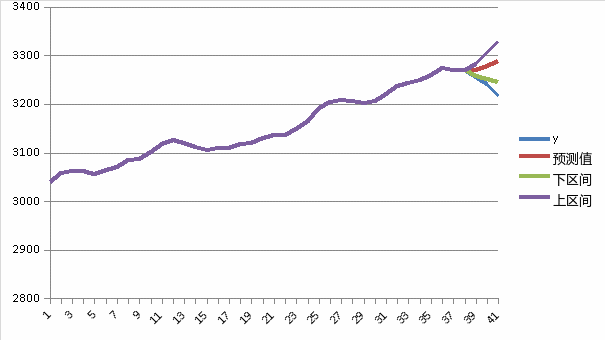
图5是从2017年6月1日至2017年8月1日水平值以及未来三期的预测值，图6是从2017年6月1日至2017年11月14日水平值以及未来三期的预测值。以下两张图讨论上涨过程中出现的短暂下滑之后继续保持上涨的趋势，对于上涨过程出现的短暂下滑，MA3的未来几期预测值一直落在模型的预测区间中，并没有突破下区间，所以可以选择一直保持持有。

图5 2017.6. 1-8. 1 ARIMA(3,1,1)模型预测=

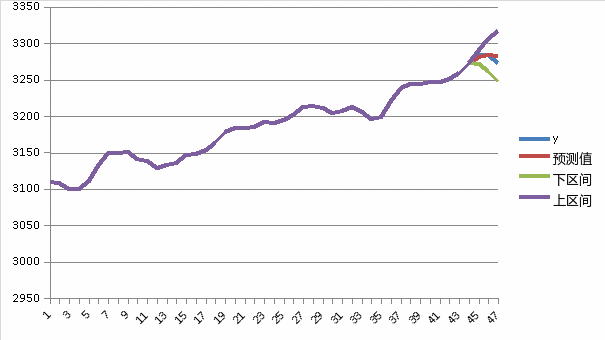
4结论

本文对上证指数中的三种情况进行讨论，然后分别对各种情况进行ARMA建模补足MA滞后特性这个缺陷，以便及时发现上涨过程中出现的拐点。一般上涨趋势过程中，大体趋势都有种线性现象，也可以对这段区间建立线性模型进行预测，经反复试验可知，线性模型的反应效果一般只能达到5期， ARIMA建模可以更及时的对原序列的数值进行回归拟合和预测。

[参考文献]

[1]王亮. 上证指数:长期均线死叉阻挡升势[J]. 股市动态分析,2019，（10）：60-63.

[2] 戴若·顾比，陈静. 上证指数下降趋势的力量[J]. 上海证券报地方级,2017（1）:40-57.

3. 朱永凤，瓦哈甫.哈尼克，卢龙辉. 移动平均交易规则对股票动态价格模型的影响[J]. 牡丹江师范学院学报(自然科学版),2018（3）,416-422.

3