浙江省丽水市莲都区教师进修学校 , 浙江 丽水 323000
摘要:错误是学生学习过程中的相伴产物,学生的错误是有价值的,是一种宝贵的学习资源和教学资源。教师在数学课堂教学中,要善待“错误”,要关注“错误”,也要包容“错误”,要用发展的眼光来看待学生学习中的错误,合理有效利用错误,让“错误”成为课堂中的“闪光点”,真正 变“废”为“宝”,从而让学生真正领悟数学方法,发展数学思维,提高数学素养。
关健词:数学;错误;资源;素养
导言:
课堂是个出错的地方,错误也是数学课堂不可避免的产物。一节真实的数学课堂教学,正是因为有了错误而精彩。教师不但可以通过挖掘学生的错误资源,及时调整课堂教学,还可以引导学生主动探究,促进学生情感的发展,增强学生的创新能力,更能加强学生对此知识的印象,提高课堂效率。因此,教师应用发展的眼光看待错误,把学生的错误当成一种生成资源,让学生在纠错、改错中感悟道理,领悟数学方法,发展数学思维,提高学生数学素养。
在数学课堂教学实践过程中,本人认为错误主要来自以下几个方面:一是来自文本的错误,二是来自教师的错误(包括教师根据自身教学经验故设的错误和不小心随机生成的错误),三是来自学生随机生成的错误。当然,一般来说,我们所碰到最多的还是来自学生随机生成的错误。作为教师,要正确面对当前初中数学课堂教学中出现的学生错误资源,要善于找到学生错误的原因,正确筛选错误,有效利用错误,让这些“错误”成为课堂中的“闪光点”,真正 变“废”为“宝”,成为学生获取新知的有效资源。
1 善待“错误”,让学生显露自己的思维过程
有探索就难免有错误发生。如果教师有意防止学生犯错,学生的思维过程就不能显露出来,教师将无法获取课堂上最真实的信息,学生将不能发挥探索、创新精神,甚至还会把错误转移到课后,造成恶性循环。因此教师要善于捕捉学生错误中显露出来的思维过程,及时调整自己的教学策略,适时为学生解疑释惑。
学生解题错误的原因是多方面的,有时错解也有其合理的一面,它往往是学生在新旧知识之间的符号、表象或概念、命题之间的联系上出现了编码错误。教师要认真剖析学生错解中的合理成分,研究它的起因,研究它与正确方法之间的联系,借机加以引导,让学生进行验证,以加深学生对知识的正确理解。
案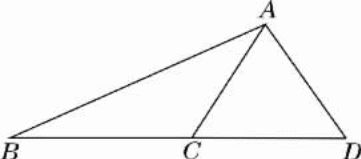 例1:学生在学习了全等三角形的判定方法“角角边”之后,很容易进行类比,而猜想得到一个错误的方法,即所谓的“边边角”。为了让学生从根本上认识到不存在这个“边边角”方法的道理,可让学生进行下面的实验操作:在硬纸片上画△ABC,要求AB=8cm,AC=6cm,∠B=30°。画好后剪下来与其他同学画的三角形进行比较,你能发现什么样结论?学生通过动手画图、剪拼,发现画出的两个三角形不能重合,也就是说,已知两边和其中一边的对角,画出的三角形不唯一。例如,在△ABC和△ABD 中(见下图),已知AB=AB,AC=AD,∠B=∠B,但它们显然是不全等的。这就直观地告诉我们,有两边和其中一边的对角对应相等的两个三角形不一定全等。从而否定了“边边角”方法
例1:学生在学习了全等三角形的判定方法“角角边”之后,很容易进行类比,而猜想得到一个错误的方法,即所谓的“边边角”。为了让学生从根本上认识到不存在这个“边边角”方法的道理,可让学生进行下面的实验操作:在硬纸片上画△ABC,要求AB=8cm,AC=6cm,∠B=30°。画好后剪下来与其他同学画的三角形进行比较,你能发现什么样结论?学生通过动手画图、剪拼,发现画出的两个三角形不能重合,也就是说,已知两边和其中一边的对角,画出的三角形不唯一。例如,在△ABC和△ABD 中(见下图),已知AB=AB,AC=AD,∠B=∠B,但它们显然是不全等的。这就直观地告诉我们,有两边和其中一边的对角对应相等的两个三角形不一定全等。从而否定了“边边角”方法
的存在。
在数学教学活动中,学生暴露出的错误,有时正是可以借用的资源,是深化数学学习、推进思维发展的良机。此案例中,教师利用错误,通过这个实验,既加深了学生对三角形全等判定方法的理解,又体会到了验证猜想正误的重要性。
2 关注“错误”,让学生在辨析中理解
教师应对学生在学习过程中所犯的错误,细加分析,并及时引导学生分析原因,寻求正确解决问题的方法。美国教育家杜威指出:“真正思考的人从错误中吸取知识比从成就中吸取的知识更多,错误与探索相联姻、相交合,才能孕育出真理。”对学生在学习过程中所犯的错误细加分析,就会发现,错误的原因或理解有偏差,或思维不够深刻,或看待问题的方式不同。
因此,教学中,学生的错误所引发的问题就是探究的切入点,关键是教师能否抓住这“错误”的契机,及时引导学生探究错因,以提高学生的辨析能力、思维调控能力,使学生在错误中反思,在探索中感悟,在发现中创新。
案例2:学习完“一元二次方程”后,一位教师在第一节复习课上出示了这样一道练习题:已知关于x 的方程(3k+1)x2-2![]() x-1=0 有两个不相等的实数根,求k 的取值范围。
x-1=0 有两个不相等的实数根,求k 的取值范围。
部分学生认为,因为方程有两个不相等的实数根,所以必须满足b2-4ac>0,即(-2![]() )2-4(3k+1)×(-1)>0,解得k>-
)2-4(3k+1)×(-1)>0,解得k>-![]() 。听完学生的分析,教师没有点评,而是让其他学生发表自己的看法。生1 马上提出:“由题意可知,此方程是一元二次方程,故还须保证二次项系数3k+1≠0,即k≠-
。听完学生的分析,教师没有点评,而是让其他学生发表自己的看法。生1 马上提出:“由题意可知,此方程是一元二次方程,故还须保证二次项系数3k+1≠0,即k≠-![]() ,故本题k的取值范围为k>-
,故本题k的取值范围为k>-![]() 且k≠-
且k≠-![]() ”。这时许多学生向生1投来了赞许的目光。很快,生2 站起来发表自己的看法,认为生1 的分析是正确的,但最后的结论还是错误的,因为k≠-
”。这时许多学生向生1投来了赞许的目光。很快,生2 站起来发表自己的看法,认为生1 的分析是正确的,但最后的结论还是错误的,因为k≠-
![]() 不在k>-
不在k>-![]() 的范围内,k的取值范围应为k>-
的范围内,k的取值范围应为k>-![]() 。教师立即表示有道理,这时课堂的气氛开始活跃起来了,教师又问:“还有其他不同意见吗?过了不一会,教室里传来了几名同学的声音:“丢了k≥0 这个条件。”教师立即加以肯定并让其中的生3 发言,生3 经过思考后说:“k 的取值范围应同时满足:k>-
。教师立即表示有道理,这时课堂的气氛开始活跃起来了,教师又问:“还有其他不同意见吗?过了不一会,教室里传来了几名同学的声音:“丢了k≥0 这个条件。”教师立即加以肯定并让其中的生3 发言,生3 经过思考后说:“k 的取值范围应同时满足:k>-![]() 且k≠-
且k≠-![]() 且k≥0。故此题k 的取值范围应该为k≥0。”
且k≥0。故此题k 的取值范围应该为k≥0。”
此案例中,教师紧扣学生可能产生的困惑,通过一波三折的过程,易错、易混的知识在学生的积极参与下分析得一清二楚,也使学生从更高层次上深化了对知识的理解。
3 包容“错误”,给学生探索的空间和时间
正确,可能只是一种模仿,而错误绝对是创新。有时学生的回答可能完全和老师预设的答案相反。遇到这种情况时,教师可以把问题暂且放一放,含笑倾听,宽容地对待错误,留给学生探索的时间和空间,让他们随着认知水平的发展和提高,自己去纠正错误,燃烧出“智慧”的火花。
案例3:在“平面直角坐标系”中,有一类题目学生经常容易出错,现举1 例:已知点P(n,-3)、点Q(5,m),直线PQ 平行y 轴,求m、n 的取值。
在讲授“平行于坐标轴的直线上的点的特点”时,教师并没有直接告诉学生结论,而是引导学生反思,并让他们自己改错,以加深其印象。在授课时,教师先让学生在平面直角坐标系中描出点(5,-3)、(2,-3)、(-1,-3)、(0,-3)、(3.7,-3),然后让学生观察这些点有什么特点,学生能发现他们都在一条平行x 轴的直线上。接着教师问他们平行x 轴的直线上的点有什么特点,学生回答这些点的纵坐标相同。在总结了平行于坐标轴的点的特点后,教师出示此题,很多学生都掉进了“陷阱”,认为n=5,m 为任意实数。当教师告诉他们答案错误时,学生都十分惊讶。教师试着让他们举个反例,再提示他们这是“两个”点所在的直线平行坐标轴。有的学生便意识到此题中还要求m≠-3,这时学生恍然大悟。教师进一步追问:“如果两个点所在的直线平行x 轴,那么这两个点的坐标有什么特点?”有的学生提到他们的纵坐标相同。马上有同学补充不但纵坐标相同,还要求横坐标不同,否则就成同一个点了。教师正准备接着讲,又有一个学生在举手,他的回答给了教师很大的启发:不仅要求纵坐标相同,横坐标不同,而且还要求纵坐标不为零,因为如果纵坐标为O,两点就在x 轴上,而不是平行于x 轴了。学生能将平行坐标轴的两点的特点补充得如此精确,这是教师万万没有想到的。
此案例中,学生经历了反思错误的思维辨析过程。当学生出错时,教师并没有直接告诉学生结论,而是引导学生反思错误、修正错误,从而使好奇心和创造力在“出错”中发出了异常的光彩,并掌握了此类问题的实质,提高对错误的免疫力,避免“重蹈覆辙”。
4 结论
总之,在数学课堂教学中,我们时常会遇到错误的伏击,然而不经历这些错误,怎能帮助学生、教师成长,体验数学的魅力。布鲁纳曾说过:“学生的错误是有价值的。”错误是学生探究的标志,也是一种学习经验。因此,我们要重新审视数学课堂,用发展的眼光来看待学生学习中的错误,合理有效利用错误,牢牢把握错误资源,抓住最富有成效的教学时刻,让学生在错误中获取更完美的知识,提高学生的数学素养。