福建省泉州市泉港区第二中学
本文为《福建省教育科学“十三五”规划2020年度立项课题》(闽教科规(2020)15号)立项课题《以高考评价体系为导向的数学建模试题的命制研究》(项目批准号:FJJKXB20-926)研究成果之一。
摘要:导数是联系初等数学与高等数学的纽带,是微积分中的核心概念之一。随着学生在学习中发展高中数学核心素养的重要性越发显现,一些能体现导数核心应用的好试题不断呈现,成为这几年高考的热点与难点。本文通过实例,就函数对称性和其导函数的关系,从试题应用的角度做一点归纳研究。
关键词:高中数学 导数应用 函数对称性 命题分析
我们知道,奇偶性是函数的重要性质之一,是高中数学函数对称性的典型代表,也是高考函数必考查的知识点。对于函数对称性的常见结论与性质,这里不再累述,本文主要结合函数对称性与导数应用的一些相关关系进行研析。
应用1 已知R上连续可导函数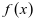 满足
满足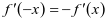 ,则
,则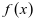 为R上的偶函数。
为R上的偶函数。
应用2 已知R上连续可导函数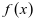 满足
满足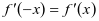 ,且
,且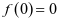 ,则
,则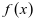 为R上的奇函数。
为R上的奇函数。
应用3 已知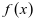 为R上连续可导函数,则
为R上连续可导函数,则
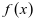 的图像关于直线
的图像关于直线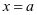 对称
对称
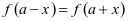

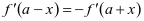
在上式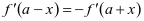 中,取
中,取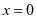 即可得到
即可得到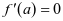 ,这样我们可得如下一个应用:
,这样我们可得如下一个应用:
应用4:若已知R上连续可导函数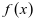 的图像关于直线
的图像关于直线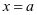 对称,则
对称,则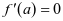
该应用可以让我们用导数来求连续可导函数图像的对称轴。
应用5 已知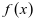 为R上连续可导函数,则
为R上连续可导函数,则
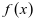 的图像关于点
的图像关于点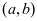 对称
对称
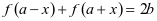

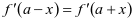
即导函数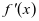 的图像关于直线
的图像关于直线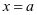 对称,再由应用3可得
对称,再由应用3可得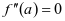 ,这样我们也可得到另一个如下应用:
,这样我们也可得到另一个如下应用:
应用6:若已知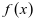 的图像关于点
的图像关于点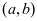 对称,则
对称,则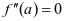 (可用二阶导来求对称中心)
(可用二阶导来求对称中心)
【例1】(2019年泉州市第二次市质检理数10)定义在R上的函数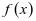 ,其导函数为
,其导函数为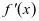 ,且
,且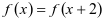 ,
,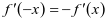 ,若当
,若当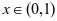 时,
时,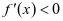 ,则
,则
A. 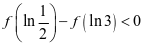 B.
B. 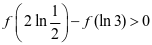
C. 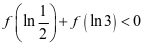 D.
D. 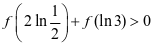
【解析】 因为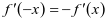 ,由应用1可得
,由应用1可得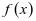 为R上的偶函数,所以图像关于y轴对称,又由当
为R上的偶函数,所以图像关于y轴对称,又由当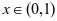 时,
时,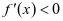 ,可得
,可得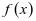 在
在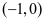 上单调递增,在
上单调递增,在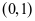 上单调递减。再由2为周期,可整理得
上单调递减。再由2为周期,可整理得
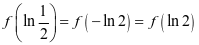 ,
,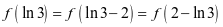 ,
,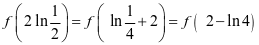 ,
,
又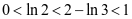 ,
,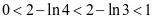 ,所以选B
,所以选B
【例2】已知函数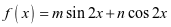 的图像关于直线
的图像关于直线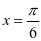 对称,求
对称,求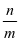 的值。
的值。
【解析】本道题的常规解法是由三角函数性质可得函数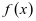 的最值为
的最值为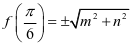 ,
,
进而得到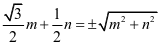 ,两边平方后整理得
,两边平方后整理得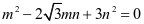 .
.
即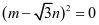 ,从而可得
,从而可得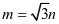 ,即得
,即得 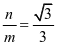 .
.
而根据应用3的应用结论,我们则可以直接采用导数法来求解,
先求得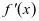 =
=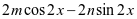 ,再由
,再由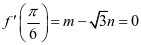 可得
可得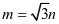 ,从而
,从而 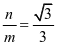 .
.
显然本题从导数应用这一思路入手,不仅事半功倍,还能让学生充分体会到通过对数学知识方法应用的深究与浸润而积淀的数学核心素养能帮他们用更广的视野去审视数学问题的解决途径。
【例3】(2020年福建省高三毕业班质量检测文数7)函数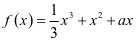 的大致图像不可能是
的大致图像不可能是
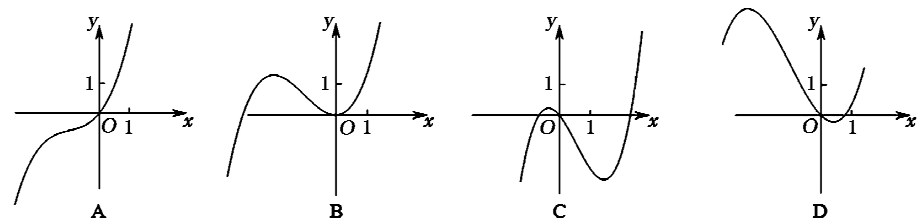
【解析】本题学生的得分率较低,主要是因为函数中带参数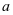 给考生带来很大的麻烦,导致同学们找不到解题的突破口。若能掌握上面几个应用内容,则容易结合三次函数图像是中心对称图形,由应用4的应用,通过
给考生带来很大的麻烦,导致同学们找不到解题的突破口。若能掌握上面几个应用内容,则容易结合三次函数图像是中心对称图形,由应用4的应用,通过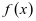 的二阶导方程
的二阶导方程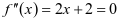 解得
解得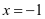 ,来求得对称中心的横坐标为-1。从而快速判断大致图像不可能是C。
,来求得对称中心的横坐标为-1。从而快速判断大致图像不可能是C。
函数对称性相关知识常在考试中作为能力型题型来考查,其题型灵活多变,一旦考生想不到关键点,就会束手无策。在高三总复习中,若能让学生多掌握些相关应用,则不仅有利于考生寻找解题突破口,还能起到事半功倍的效果。