北方铜业股份有限公司 山西省垣曲县 043700
摘要:目前,关于崩塌落石的计算理论主要分为经验分析法和运动学分析方法。经验分析法中具有代表性的为前苏联尼米罗依尼什维里教授在大量野外现场试验基础上提出的落石运动速度的方法,但该方法依据的现场试验性较强,对于边坡坡度变化、距离拟保护目标的远近以及坡面植被情况等较难综合考虑。而运动学分析方法是对落石局部过程运动状态的描述。该方法是以牛顿三大运动定律和碰撞理论为指导,对大量的模型试验和现场试验的研究结果进行分析,结合运动学公式对落石运动的轨迹进行表述,该方法比经验分析方法更多地考虑边坡的特性和落石的运动轨迹之间的相互关系。因此,本文将基于运动学原理对落石运动轨迹进行计算分析,并将其与数值模拟的结果进行对比,以便于探讨落石的落点分布、运动速度、弹跳高度及动能分布等问题,并对相关的治理设计提出建议。
关键词:地质灾害;崩塌落石
1 概述
危岩落石是我国山区一种多发地质灾害,其失稳破坏过程也称为崩塌,一般是指地质体在重力作用下,从高陡坡突然加速崩落或滚落(跳跃),具有明显的拉断和倾覆现象。崩塌的地质体通常为大体积岩体或土体;崩塌落石则是斜坡和高陡坡上的个别危岩体在重力和其他外力作用下,突然向下滚落的现象,其运动轨迹和动能的大小是防护网设计的关键因素,直接影响到防护网实施效果的成败。因此,对崩塌落石运动特征的研究,可以为崩塌落石工程治理设计提供依据,具有重大意义。
2 崩塌落石的运动模式
落石的整个运动过程一般可分为坠落、碰撞、滑动和滚动四个阶段。坠落一般认为是落石在自重作用下不受阻挡失稳的自由落体运动,在此,简化为不考虑空气阻力和升力的影响;碰撞弹跳是落石运动过程中最为复杂和不确定的,一般可简化为刚体碰撞;滑动为落石沿着某一斜面运动;滚动可简化为圆形刚体在某一斜面上的摩擦运动。
2.1 坠落
落石坠落可认为是自由落体运动。根据运动学原理,在任意高度h下落时,下落速度和下落时间为:
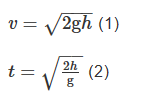
在上述时间内的位移为:
![]()
其中,g为重力加速度,m/s2;v为落石的自由落体速度,m/s;v0为落石初始速度,m/s;h为垂直位移,m;H为t时间内总位移,m。
2.2 碰撞弹跳
落石做碰撞弹跳运动时,可假定为做斜抛运动,即以一定的初速度和水平方向成一定角度抛出,运动轨迹为抛物线。
落石碰撞后会损失部分能量,我们可以用恢复系数法来描述碰撞后落石的运动,这样可以避免碰撞过程中非线性变形以及摩擦问题的直接讨论,便于在工程实践中应用。
根据碰撞理论,落石第i次碰撞后其初始速度为:
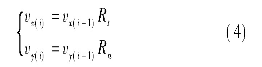
其中,Rt为沿x方向的恢复系数;Rn为沿y方向的恢复系数。可根据表1取值。
由运动学基本原理,落石与基岩碰撞后,速度方程为:
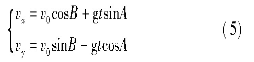
其中,A为坡面与水平面的夹角,(°);B为落石开始弹跳时初速度方向与边坡坡面的夹角,(°);vx为落石任一时刻沿x方向的速度分量,m/s; vy为落石任一时刻沿y方向的速度分量,m/s; t为碰撞发生开始至任一计算点的时间,s。
落石碰撞后的运动轨迹方程为:
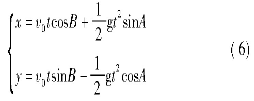
其中,x为x方向上的位移分量;y为y方向上的位移分量。
表1 恢复系数取值表
| 法向恢复系数 | 切向恢复系数 |
| 0.25~0.75 | 0.88~0.98 |
| 0.15~0.37 | 0.75~0.95 |
| 0.15~0.37 | 0.75~0.95 |
| 0.12~0.33 | 0.30~0.95 |
| 0.12~0.32 | 0.65~0.95 |
| 0.10~0.25 | 0.30~0.80 |
| 0.10~0.30 | 0.50~0.80 |
2.3 滑动
落石在斜坡坡面上,其自重下滑分力大于摩擦力时,在任意垂直位移h,其速度v可用式(7)表示:
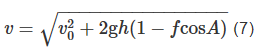
其中,v为落石滑动速度,m/s;f为摩擦系数,无量纲;其余符号同前。
2.4 滚动
当落石沿斜坡面发生滚动运动时,为了便于计算分析,如前所述,可将落石滚动简化为圆形刚体在斜面上的摩擦运动,此时,对于任意位置L有:
![]()
其中,v为落石滚动速度,m/s;C=m(m+I/R 2 ) C=m(m+Ι/R2) ,表示和落石的质量与形状有关;I为落石的转动惯量;ϕc为滚动摩擦角;fr为滚动摩擦系数,fr=d/R=tanϕc其与落石的质量、形状、速度、边坡的坡度和坡面覆盖层或者基岩的力学性质有关。
2.5 动能的计算
落石最后具有的总动能可通过式(9)计算,以便为防护设计提供依据。
![]()
其中,E为落石具有的总动能,J;I为落石的转动惯量,kg/m2;ω为落石的转动角速度,rad/s。
3结论
落石运动的影响因素很多,运动形式也非常复杂,要精确求解危岩的路径方程难度很大。本文基于运动学原理,根据落石的运动模式简化计算了落石的运动轨迹,并与数值模拟的计算结果加以对比,可得以下两点结论:
1)落石运动路径和预测的基础为危岩崩落后的起始运动状态,起始状态可通过运动学原理计算求得。基于运动学原理的运动方程基本能够描述理想情况下落石的运动轨迹。
2)Rockfall数值模拟的结果与理论计算较为吻合,两者的计算结果可相互验证,以便为防护设计提供依据。
基于运动学计算和数值模拟计算,不仅能够计算落石沿坡面的完整运动路径,而且也能够预测落石在坡面的跳跃段位置和滚滑段位置。
根据上述计算、分析,在实际工程设计中,可选择落石弹跳高度小、动能小、便于施工的位置,结合防治要求,灵活设置防护网。但本文也存在有不足之处。实际上,崩塌落石的运动轨迹受到多种因素的影响,比如:落石的形状、落石运动过程中的碎裂以及其相互碰撞对落石运动轨迹的影响等本文均未考虑,这方面的工作应当深入研究,以便建立完整的崩塌落石评价体系。
参考文献
[1] 胡厚田.崩塌与落石[M].北京:中国铁道出版杜,1998.
[2] 胡厚田.崩塌落石研究[J].铁道工程学报,2005(z1):387-391.
[3] 陈洪凯,唐红梅,王蓉.三峡库区危岩稳定性计算方法及应用[J].岩石力学与工程学报,2004,23(4):614- 619.
[4] 陈洪凯.三峡库区危岩综合治理技术及运用[J].地下空间,2002,22(2):97-101.