高新技术研究所,山东省青州市, 262500
摘要: 为了在车辆产品选型中对车辆产品性能与厂家研发生产能力等因素进行评判,本文应用系统工程中的层次分析与模糊评价相结合的方法,综合考虑了定性与定量因素的影响,研究了一种对整车给出定量的评价分数的方法,以减少人为因素的影响,公平合理的完成选型工作。
关键词: 选型 多层次 模糊 评判
部队在车辆产品选型过程中,常采用专家评审的方法,按得票多少给出倾向性意见,但车辆选型中不确定因素很多,单凭借专家的经验是很难综合出一个准确的评价分数。需要探讨出一种应用系统工程中的层次分析与模糊评价相结合的方法,对有试验数据的因素,给出定量分数,对一些需靠专家经验来综合分析评价的因素,采用模糊数学的方法,综合定性与定量因素,对整车给出一个定量的评价分数,最大程度上减少人为因素的影响,公平合理的完成选型工作。
鉴于车辆产品选型评估的模糊性和相对性,本文提出基于模糊综合评判法[1,2]的车辆产品选型评估模型,把评价指标和评价对象划分成递阶结构层次,建立多层次的评价指标体系。对同一层次上的元素,通过成对的相互重要程度比较,组成一致性模糊判断矩阵,相应于该模糊矩阵主特征值的主特征矢量的大小即表示了各评价对象的优先级顺序。
经广泛征求专家意见,反复交流信息,本文运用主成分逐步回归法选择影响车辆产品选型且相互独立的指标,以某轻型越野车选型为例,建立整车评价体系因素树[3],见图1。
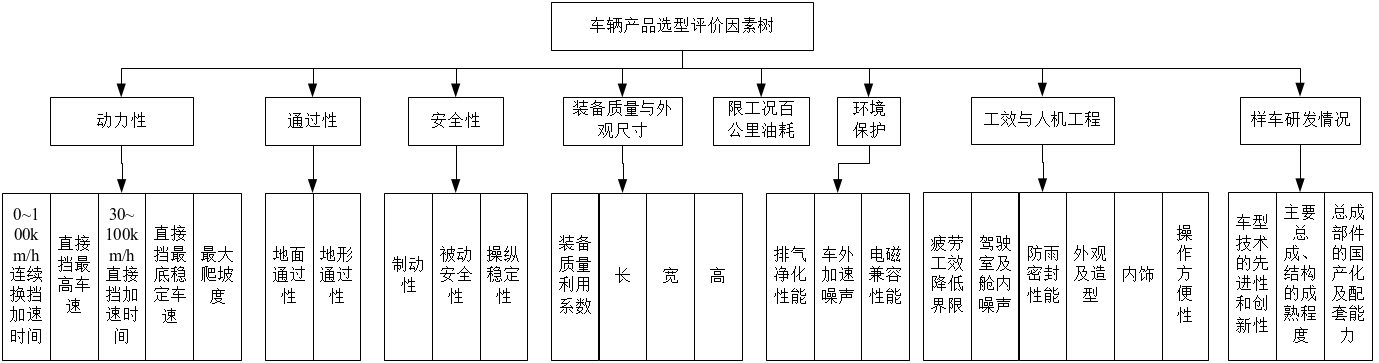 图1 评价指标因素树
图1 评价指标因素树
首先确定车辆产品选型各评价因素因子之间的优先序列问题,即权重集:A={a1,a2,…,am},权重ai:因素对上一级因素的“重要程度”,并满足正数和归一性要求,即∑ai=1,ai=0。本文用模糊统计的方法确定A,步骤如下:首先由专家根据经验、推理确定各级评价指标因素集中各因素Ui的“相对重要程度”(表1中的权重评语),由此可以统计得出Ui在权重评语集V={特别次要、很次要、次要、一般、重要、很重要、特别重要}上的隶属频率,即得出隶属频率向量Ci=(Ci1,Ci2,Ci3,Ci4,Ci5,Ci6,Ci7),i=1,2,3,4,…,l(或p、q、r)。由表1查出各权重等级隶属度,则计算各因素的得分值Ai:
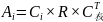 (1)
(1)
公式(1)其中:C权为权重等级矩阵,C权=(0,0.20,0.35,0.50,0.65,0.80,1.00),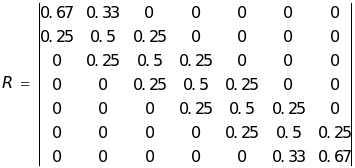 ,确定权重A。
,确定权重A。
表1 因素权重模糊综合评价法子集
等级 | 特别次要 | 很次要 | 次要 | 一般 | 重要 | 很重要 | 重要 |
0 | 0.67 | 0.25 | 0 | 0 | 0 | 0 | 0 |
0.20 | 0.33 | 0.5 | 0.25 | 0 | 0 | 0 | 0 |
0.35 | 0 | 0.25 | 0.5 | 0.25 | 0 | 0 | 0 |
0.50 | 0 | 0 | 0.25 | 0.5 | 0.25 | 0 | 0 |
0.65 | 0 | 0 | 0 | 0.25 | 0.5 | 0.25 | 0 |
0.80 | 0 | 0 | 0 | 0 | 0.25 | 0.5 | 0.33 |
1.00 | 0 | 0 | 0 | 0 | 0 | 0.25 | 0.67 |
1.3.1 一级评价数学模型
(1)因素集:U={u1,u2…um},um因素,i=1,2,⋯,m。
(2)方案集:F={f1,f2…fm},fi:方案,i=1,2,⋯,s。
(3)评语集:V={v1,v2…vm},vj:评语,j=1,2,⋯,n。其中:C权为权重等级矩阵。
(4)单因素评价矩阵。首先确定方案集F中各方案fi对最低层评价指标因素集U中的因素ui的相对贡献程度。分两种情况:情况1:对定性评价的指标,确定方案对评价集V中某评语vi (i=1,2,…,7)的隶属关系(即属于很好、较好或好、…);情况2:对定量计算或试验得到的指标,计算方案对因素ui的满足度Pi(Pi 1)。
①确定方案的单因素评判集。单因素评判集的形式为:ri=(ri1,ri2,ri3,ri4,ri5,ri6,ri7),其中rij对第i个因素ui而言,方案对评价集V中第j个满足度的隶属度,rij[0,1]。
②确定单因素评价矩阵。由m个单因素评判集组成单因素评价矩阵R,见公式(2)。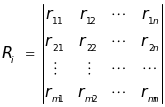 (2)
(2)
1.3.2二级评价数学模型
二级(最低级)因素综合评价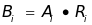 ,一级因素综合评价
,一级因素综合评价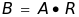 。其中,
。其中,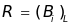 ,即公式(3):
,即公式(3):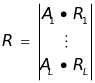 (3)
(3)
L为一级因素的个数。对于多级因素树,用以上方法,由最底层向上一级综合,可得到最上层的综合值。综合得分E为:E为:E=B×FT (4)
其中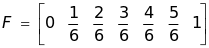 。
。
A厂家车型为A型车,B厂家车型为B型车,方案集为{PA,PB}。
采用模糊统计方法确定各因素集的权重,以动力性为例,根据统计12位专家对表3填写的结果,得到各因素Ui在权重评语集V“特别次要、很次要、次要、一般、重要、很重要、特别重要”上的隶属频率,见表4(以直接挡最高车速为例):
表3 相对重要程度关系表
因素 | 0-100km/h连续换挡加速时间 | 30-100km/h直接换挡加速时间 | 直接挡最高车速 | 直接挡最底稳定车速 | 最大爬坡度 |
重要程度 | 重要 | 特别重要 | 重要 | 一般 | 一般 |
表4 直接挡最高车速隶属频率统计
等级 | 特别次要 | 很次要 | 次要 | 一般 | 重要 | 很重要 | 特别重要 |
重要程度 | 2 | 4 | 4 | 0 | 1 | 0 | 1 |
根据表4计算得出隶属频率向量为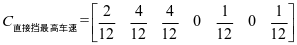 ,
,
根据公式(1)计算得分值: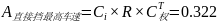 。同理可得出A2、A3、A4、A5的分值,并得到权重向量:(0.322,0.278,0.2,0.1,0.1)。
。同理可得出A2、A3、A4、A5的分值,并得到权重向量:(0.322,0.278,0.2,0.1,0.1)。
对于定量指标,以动力性为例:A型车与B型车试验数据如下:
表5 动力性指标数据
车 型 | A型 | B型 |
0-100km/h 连续换档加速时间(s) | 14.3 | 19.8 |
30-100km/h 直接换档加速时间(s) | 26.3 | 27.7 |
直接档最高车速(km/h) | 155.1 | 138 |
直接档最低稳定车速(km/h) | 8 | 7.6 |
最大爬坡度(°) | 22.8 | 14.2 |
根据评价公示将表5试验数据归一化,得到A型车动力性的满足度向量为:(0.964,0.88,1,0.87,0.858),B型车动力性的满足度向量为(0.757,0.859,0.86,1,0.755)。
由表2,插值计算得到动力性指标的单因素评价矩阵:
A型车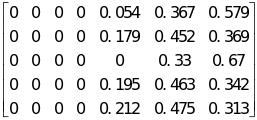 ,B型车
,B型车 。
。
因素树最底层起,按照公式(3)计算综合评判结果,仍以动力性计算为例,由式
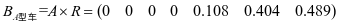 ,
,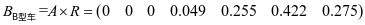 。
。
逐层计算,最后得到第一层综合评判结果,用公式(4)计算综合得分E 为:E BFT 。
EA型车AR0.56,EB型车AR0.72。由计算结果可以看出,B型车的整体得分较高,说明B型车综合水平较A型车高,应优先选用。
(1)采用层次分析与模糊评判的综合分析方法,可以较为全面的量化考虑定量与定性因素对方案整体水平的影响,最大程度上减少人为因素的影响。
(2)权重值对最后评价分数有重要的影响,宜采用专家评分的方法以提高其合理性与准确性。
(3)评价应尽量以可试验定量参数为评价因素,减少定性评价指标的比例。
参考文献
[1]刘广萍,吴辉. 层次分析法在模糊控制中的应用[J],佳木斯大学学报. 2017.3 (7):26-29.
[2]汪培庄,韩立岩. 应用模糊数学[M]. 北京经济学院出版社,1989.
[3]刁增祥. 军用越野汽车效能评价体系研究 [硕]. 吉林工业大学汽车学院,2016.