陕西省西安中学
内容摘要:“线面垂直”问题是高中数学《立体几何》部分的重点内容,学生学习了点线面位置关系之后,在空间中要对具体的线面特殊位置关系进行判定,“平行”和“垂直”是空间中直线和平面的特殊的位置关系。学生在学习过线面垂直的判定定理之后,具体到做题时,会有一些直线之间的关系不太好寻找,从而没法利用判定定理。本文通过具体的问题,提出巧解这类的问题的方法,希望可以帮助学生解决做题中的困难。
关键词:线面垂直,判定定理,三垂线定理
线面垂直的判定定理:如果一条直线和一个平面的内的两条相交直线都垂直,那么该直线与此平面垂直。
即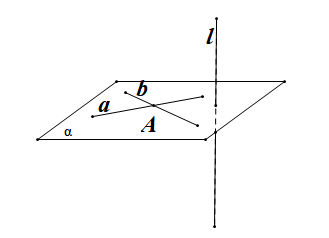 :若直线
:若直线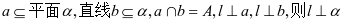 .如图所示.
.如图所示.
由该定理可知,要证明直线和平面垂直,关键是找到平面内的两条相交直线都和这条直线垂直。我们看下面一道题目。
例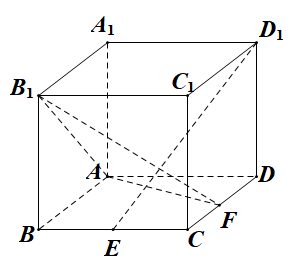 :如图所示,在棱长为1的正方体
:如图所示,在棱长为1的正方体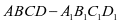 中,点
中,点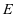 是棱
是棱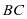 的中点,点
的中点,点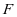 是棱
是棱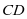 上的动点.试确定点
上的动点.试确定点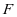 的位置,使得
的位置,使得
分析:本题是一道探索性的问题,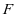 为动点,导致的结果是直线
为动点,导致的结果是直线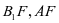 为动直线。于是在三角形
为动直线。于是在三角形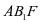 中,只有
中,只有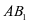 为定直线,要使直线
为定直线,要使直线 ,必然先有
,必然先有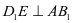 ① 关注到直线
① 关注到直线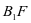 为正方体内部的直线,而直线
为正方体内部的直线,而直线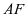 为正方体表面的直线,应该要想到去证明
为正方体表面的直线,应该要想到去证明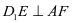 ②(定动都有首选定,体面共存首选面)
②(定动都有首选定,体面共存首选面)
对于①和②,都是异面直线垂直问题,将其转化成线面垂直比较方便证明。对于①,寻找平面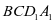 即可,对于②,注意到
即可,对于②,注意到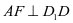 ,所以寻找平面
,所以寻找平面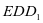 即可。
即可。
证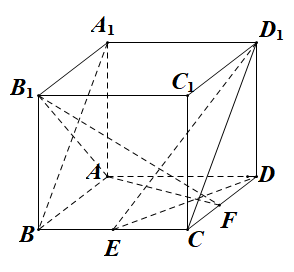 明:连接
明:连接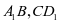 ,
,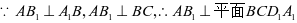
![]()
连接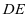 ,要使
,要使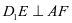 ,只需
,只需 ,
,
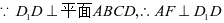 ③,所以只需
③,所以只需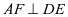 即可,在正方形
即可,在正方形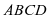 中,因为
中,因为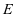 为
为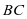 中点,所以当
中点,所以当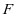 为
为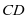 中点时,有
中点时,有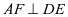 ④,由以上③和④,证明了
④,由以上③和④,证明了 ,所以
,所以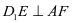 .综合以上证明得出:当
.综合以上证明得出:当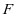 为
为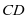 中点时,有
中点时,有
在做题中,不少学生对证明异面直线垂直的过程中,寻找与其中一条直线垂直的平面表示困难重重,在这里,几何中重要的定理——三垂线定理,对寻找平面可以提供帮助。
 三
三 垂线定理:平面内的一条直线,如果与穿过这个平面的斜线在该平面内的投影垂直,那么也和这条直线垂直。简记之,就是“垂直于投影,垂直于斜线”。 如上题,为了证明①,可以在平面
垂线定理:平面内的一条直线,如果与穿过这个平面的斜线在该平面内的投影垂直,那么也和这条直线垂直。简记之,就是“垂直于投影,垂直于斜线”。 如上题,为了证明①,可以在平面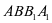 中寻找直线
中寻找直线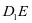 的投影,显然为
的投影,显然为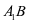 ,
,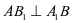 ,
,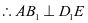
对于②,要使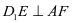 ,只需
,只需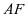 垂直于
垂直于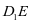 在平面
在平面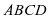 内的投影即可,显然为
内的投影即可,显然为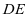 ,于是只要
,于是只要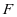 为
为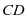 中点即可。
中点即可。
由于北师大版的高中数学课本中没有对三垂线定理的介绍,所以要求考试中不得直接使用三垂线定理。但是如果知道这个定理,那么斜线与斜线在平面的投影组成的平面就可以作为证明异面直线垂直的过程中“线面垂直”中的平面了。如上题中,证明①,就是证明 ,证明②,就是证明
,证明②,就是证明 ,这样大大加快了做题进度,也使得困难问题变得明朗了起来。
,这样大大加快了做题进度,也使得困难问题变得明朗了起来。
姓名:范欣;出生年月:1986.5 ;性别:女;籍贯:河北省;职务:高中数学教师;职称:一级教师;单位:陕西省西安中学;研究方向:中学数学