【 1】国网池州供电公司
【2.3】深圳市科中云技术有限公司
【摘要】文章提出了一种基于ARIMA模型的负荷估计算法。根据台区配电负荷日峰值数据表现出的周期性和渐变性,建立基于温度-负荷回归模型残差的ARIMA模型的台区配变负荷峰值预测方法。建立溫度-负荷回姑模型,以日最高气温为自变量,对负荷数据进行回归分析,将回归分析得到的数值与真实数据进行比较得到回归残差,建立回归模型残差序列的ARIMA模型,并进行参数估计计算,即可得到待预测日负荷预测值。根据研究成果,可以将开发的负荷估算算法与状态估算或其他网络操作工具集成在一起,更好地监视和控制配电网络,为电力系统提供服务。
关键词;配电台区;负荷预测;ARIMA模型
【引言】
随着国家能源高效开发和利用战略决策转型,电力必然成为未来经济发展的能源基础。当前,随着智能配电网建设的提速,负荷预测领域也引入了大数据技术,利用大数据技术中的数据挖掘、模式识别及关联分析等关键技术,从海量历史负荷数据中挖掘出具有潜在价值的信息,实现配电网负荷的精确预测逐渐得到了广泛关注。与上述电网相比,台区配电负荷的数据呈现出明显的区域性特点,且存在较少的统计数据种类、较差的数据质量、难以量化影响因素等缺陷。本文选择以台区日负荷峰值为样本,开展基于日负荷峰值时间序列的配电台区中负荷预测的研究,但因传统的冋归分析不再适用存在一定周期性的日负荷峰值,木文将采用基于负荷预测误差回归模型开展台区负荷预测的研究。
1、台区负荷预测影响因素
与区域电网相比,配电台区负荷预测的关键问题在于其影响因素更加难以分类和量化,能够获得的各种统计数据少且数据质量较差,这些因素使得台区配变负荷的预测成为一大难题。根据经验,影响配电台区负荷预测准确性主要存在经济、时间、气象等若干因素。低压配电台区存在许多大量分散负荷,负载对电网产生随机干扰,但这种干扰一般可被视为白噪音,其期望为零,方差恒定,且这些随机干扰是无法精准预测的,干扰源对负荷预测的定性分析及定量计算是非常困难的。
2、台区负荷数据的处理
台区配电负荷的信息由安装在配电终端采集并上传至电力系统的集采系统,利用台区每日最大负荷构成日负荷峰值时间序列。然而,配电台区受采集终端不稳定、外界环境变化及突发情况干扰等影响,可能导致负荷数据难以获取或失真等各种异常情况的发生,直接影响了负荷预测模型的稳定性和预测精度。因此,获取原始负荷数据之后,需要对数据进行鉴别和处理,按照下列步骤进行处理。
Stepl:设台区日负荷峰值时间序列,选取日附近相邻的3期数据的平均值生成一个新的数列。设台区日负荷峰值时间序列为:Yt=(Y1,Y2,…,Yn),选取t日附近相邻的3期数据的平均值生成一个新的数列,当j=1和n时,即时间序列为首端期,有成立。
Step2:定义数据偏离率Pt为t日数据偏离新数列Yt的比率:
Slep3:取阈值ε,为当pt<ε时,t日数据Yt可视为正常值;当ρt≥ε时,t日数据Yt被视为失真数据,暂时将其从数列Yt中剔除。
Step4:使用线性插值法对缺失数据进行修复。按照缺失数据的特点将其分为单一缺失与多个缺失两种情况。假设第i点为单一缺失数据点,将其相邻的两个数据的平均值作为修复值:Yi=Yi-1+Yi(J+1)/2;当出现数据多个缺失时,设相邻缺失点数量为k个,起始点为i,则缺失数据序列如(Yi,Yi+1,…,Yi+k+1)所示,设其中任一缺失点为Yi+j(0≤j≤k-1),取r=max(j,k-j),将缺失值修复为:Yi+j=(Yi+j-r-1+Yi+j+r+1)/2。
3、基于温度回归残差的台区负荷预测
3.1负荷特性分析
以某省电网某地区2020年7月1日至7月31日的负荷数据(剔除了节假日的负荷数据)为例进行用电负荷与气象因素关系的分析。具体如图1所示。
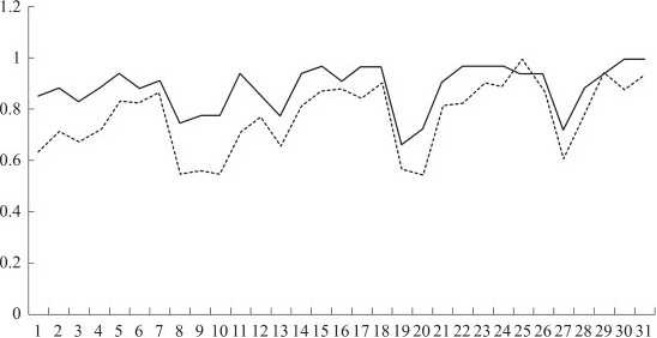
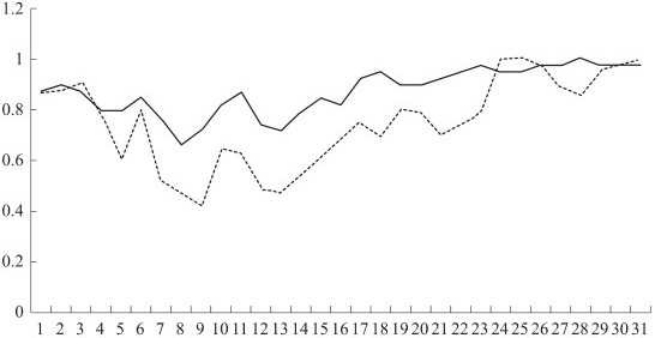
__最高温度 ..最大负荷 (a)居民负荷 (b)商业负荷
从上图可知,日最大负荷与日最高气温的变化趋势非常相似,两者变化曲线具有一定的正相关性,即负荷的峰谷点与温度的峰谷点基本重合。显然,日最大负荷与日最高气温有较强的正相关性,可利用上述特点采用基于温度-负荷冋归的分析方法对配电台区的负荷进行较为准确的预测,
3.2负荷回归残差预测模型
基于所获取的历史负荷数据及温度信息,建立如下负荷预测模型:
Lk=axTk+b+εk(1≤k≤n)(1)
式中Lk为第k天最大负荷;Tk为第k天的日最高气温;a和b分别为回归系数和回归常数,可采用
最小二乘拟合方法估计得到;由其他各种因素共同引起的第k天负荷的随机波动为给;n为历史样本天数。
式(1)描述的模型并没有充分计及配电台区负荷的周期性变化趋势,所以,由式(1)处理后获得的回归模型残差序列{εk}中必然包含周期成份构成的非平稳序列,需对回归模型残差序列进行平稳化处理,用周期性差分消除周期变化趋势,而并不能直接对回归模型残差建立ARMA模型。
冋归模型残差序列{εk}通常以周为周期进行变化,为消除周期变化趋势,可以采用周期性差分算子{(1-B7)εk}(B为延迟算子)进行计算,这样便能得到消除周期变化趋势的平稳序列,从而可以采用时间序列分析方法的ARMA(自回归滑动平均)建立如下的负荷预测模型:(2)
式中,μk为白噪声,未知参数θ1,θ1的估计为:
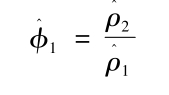
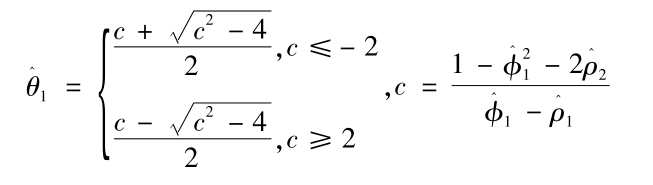 (3) (4)
(3) (4)
样本自相关系数ρk可以根据以下公式求得:
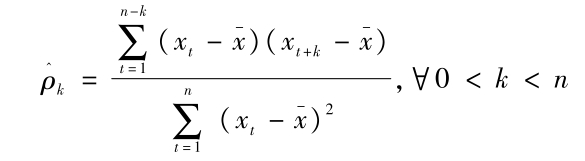 (5)
(5)
显然,本文构造的基于负荷回归残差预测模型首先基于负荷与相应的温度数据建立了回归模型,再发展回归模型残差的AKIMA模型并对回归模型进行修正,这样就较好地考虑了日最高气温对负荷的影响。
4算例分析
基于某省电网某地2020年5月I日至2020年7月31日的负荷数据、日最高气温数据采用式(2)模型对2020年8月1日至2020年8月31日的日最大负荷进行预测。
首先,建立温度-负荷回归模型,以日最高气温为自变量,对负荷数据进行回归分析,建立回归模型如式(1)所示,得到第k天的最大负荷预测值Lk。其次,鉴于Lk与实际历史数据是有误差的,因此将其与真实数据Lk进行比较,得到第k天的冋归残差εk=Lk’-Lk。最后,建立第k天的回归模型残差序列的ARIMA模型,并进行参数估计计算。最后,根据预测日的温度得到待预测日的负荷粗略估计值Lk=aTk+b+εk,再利用回归模型残差序列的ARIMA模型预测待预测日k的冋归模型预测残差ε^k,即可得到待预测日k的负荷预测值L^k+ε^k。
将本文所述的方法与传统ARIMA方法预测结果进行比较,如图2所示。
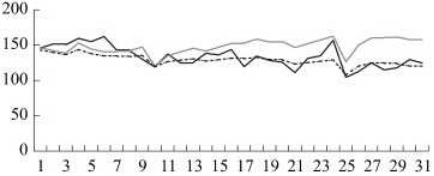
—实际负荷一ARIMA……本文方法
图2不同预测结果对比图
由图可见,本文所提出的预测结果更加接近实际负荷水平,预测准确度达到95.5%,优于传统ARI-MA模型预测87.6%的预测精度。
5结束语
气象因素尤其是气温是影响配电台区负荷预测准确性的重要因素。受当前配电自动化现状的制约,配电台区的负荷预测不可能采用较为复杂的人工智能算法。传统的温度-负荷回归模型则过于简单,而传统ARIMA预测模型则未能考虑气象因素,两者的预测精度都不够高。本文提出的模型充分考虑了影响负荷的重要因素一日最高气温,利用温度-负荷线性回归模型首先对负荷进行粗略估计,再用所提出的线性回归模型残差的ARIMA模型对线性回归模型预测结果进行修正,提高了负荷预测的精度,为配电台区的中短期负荷预测提供了一种实用化的方法。
参考文献
[1]王刚,杨晓辞,张志军,等.基于深度神经网络与权值共享的工业园区负荷预测[J].电测与仪表,2021(1).
[2]獎唯钦,张伟,李勇钢,等.基于改进人体舒适指数的微电网超短期负荷预测[J].广东电力,2017,30(4):137-142.
[3]李夏成..配电台区时冋序列大数据负荷预测技术研究[D].北京:华北电力大学,2017.
4