四川省贸易学校 625000
动能定理是力学中一条重要规律,经常用来解决有关的力学问题。下面举几个例题来说明它的应用。
﹝例1﹞质量是0.2千克的子弹,以400米/秒的速度水平射入厚度是20毫米的钢板,射穿后的速度是300米/秒。求钢板对子弹的平均阻力。
解:子弹穿过钢板时所受的外力就是钢板的阻力f,外力所做的功W=-fs,其中s为钢板的厚度。根据动能定理得到
 fs=
fs=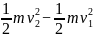
所以
f=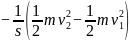
=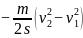
=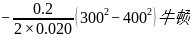
=3.5х105牛顿
答:平均阻力是3.5х105牛顿。
﹝例2﹞ 一架新型喷气式战斗机的质量是1. 50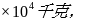 发动机的推力是1.11
发动机的推力是1.11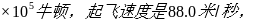 滑跑距离是671米,计算飞机起飞时受到的平均阻力。
滑跑距离是671米,计算飞机起飞时受到的平均阻力。
Fs fs=
fs=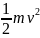
F f=
f=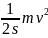
f=F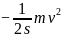
=1.11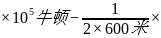 1. 50
1. 50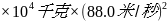
 1.42
1.42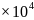 牛顿
牛顿
答:飞机起飞时受到的平均阻力1.42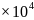 牛顿。
牛顿。
这个例题也可以应用牛顿第二定律和运动学公式来解。动能定理的公式是在牛顿运动定律和运动学公式的基础上推导出来的,所以同一题目可以用两种方法来解,求得的结果是相同的。由于动能定理不涉及物体运动过程中的加速度和时间,因此应用它来解题往往比较方便。
﹝例3﹞一辆10吨的载重汽车,开上一个坡路,坡路长=200米,坡顶和坡底的高度差h=20米。汽车上坡前的速度是20米/秒,上到坡顶时减为10米/秒。汽车受到的平均阻力是车重的k=0.05倍。求汽车的牵引力。(取g=10米/秒2)
解:汽车受到的外力有牵引力F、重力mg和阻力f.牵引力所做的功W1=Fs.重力所做的功W2=mgsinθ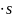 =
= mgh,其中θ是坡路的倾角。阻力所做的功W3=
mgh,其中θ是坡路的倾角。阻力所做的功W3= kmgs,根据动能定理得到
kmgs,根据动能定理得到
W1 + W2+ W3=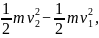
或者
Fs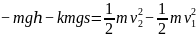
解出F得到
F=mg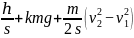
=10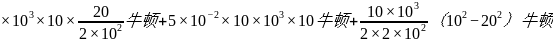
=7.5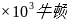
答:牵引力为7.5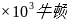
从上面的例题可以看出,在利用动能定理来解力学问题的时候,先要分析物体的受力情况,并据此列出各个力所做的功,然后即可利用动能定理来求解。
[例4]在水平面上有两个质量不同而具有相同动能的物体,它们所受的阻力相等。这两个物体停止前经过的距离是否相同? 它们停下来所用的时间是否相同?
解:Fs1=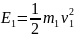 (1)
(1)
Fs2=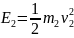 (2)
(2)
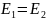
与(2)相比
s1/ s2=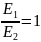
所以停止前经过的距离相等。
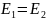
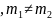 ,
,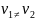
s=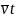 =
=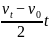
末速度为零,初速度不同,位移相同,则时间不同。
答:这两个物体停止前经过的距离相同,它们停下来所用的时间不同 。