厦门市思明区观音山音乐学校
摘要:关注数学核心知识的教学设计、实践与反思,注重学生的深度理解、成长与独立,笔者挖掘函数与方程教学的本质困难,总结思维层面的可操作的程序,形成易于学生迁移运用的方法,促进教学减负提质。
关键词:二次函数 一元二次方程 教学实践
一、教学实践
学生在“一次函数”一章已经了解了一次函数与一元一次方程、一元一次不等式、二元一次方程组的联系。人教版数学九年级上册第二十二章专设一节,通过探讨二次函数与一元二次方程的联系,再次展示函数与方程的联系。先是从二次函数解析式的角度看一元二次方程,认识二次函数与一元二次方程的联系[1]。例如,已知二次函数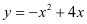 的值为3,求自变量
的值为3,求自变量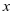 的值,可以看作解一元二次方程
的值,可以看作解一元二次方程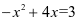 (即
(即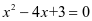 )。反过来,解方程
)。反过来,解方程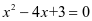 又可以看作已知二次函数
又可以看作已知二次函数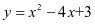 的值为0,求自变量
的值为0,求自变量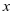 的值。再观察函数图象(抛物线),借助几何直观,从函数图象来看,如果抛物线与
的值。再观察函数图象(抛物线),借助几何直观,从函数图象来看,如果抛物线与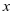 轴的公共点的横坐标为
轴的公共点的横坐标为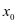 ,那么当
,那么当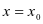 时,函数值为0,因此
时,函数值为0,因此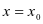 是方程
是方程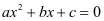 的一个根。二次函数
的一个根。二次函数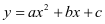 的图象与
的图象与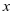 轴的三种位置关系与一元二次方程
轴的三种位置关系与一元二次方程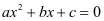 的根的三种情况相对应。
的根的三种情况相对应。
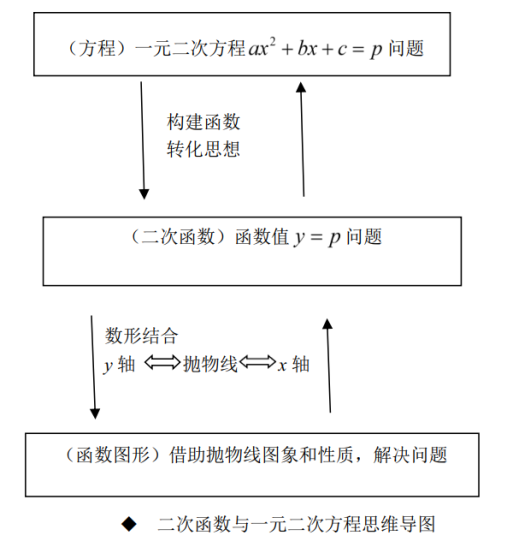
二、几点思考
1. 教学准备
方程教学的准备。掌握一元一次方程、二元一次方程组、分式方程、一元二次方程一般解法等基本技能,提高含参方程的解法、方程类型分类、方程的根的情况的讨论等综合能力。特别对于一元二次方程教学,课本上介绍的四种解法:直接开平方法、配方法、公式法、因式分解法,在实践中多考虑因式分解(十字分解)和公式法。例如:增长率问题多用直接开平方法,足球联赛问题等其它应用题多用因式分解法。在方程计算题中,除非符合配方法的特征,否则优先考虑因式分解和公式法。对于公式法的理解不局限于记忆公式,学有余力的同学应该能独立推导公式,并且掌握根与系数的关系。公式法的优势在于能直接求得具体的两个根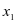 ,
,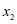 ,有时候
,有时候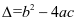 不是完全平方式不能开尽方时,需要将两根和
不是完全平方式不能开尽方时,需要将两根和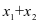 ,两根积
,两根积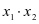 整体代入考虑。
整体代入考虑。
函数教学的准备。从数轴、平面直角坐标系的规范画图,到正确写出点的坐标,根据坐标描点,图形与坐标的基础知识要求学生掌握点坐标的定义与表达,能够熟练操作工具建立规范的平面直角坐标系。二次函数的学习是以已学函数内容为基础的。从八年级下册“一次函数”的学习到九年级上册“二次函数”的学习,中间相隔了一段时间,函数的概念,描点法画函数的图象等在本章中都要用到,因此要注意复习这些知识[2]。研究函数问题的一般思路是:先研究函数三种表现形式:解析式、表格、图象,初步感受自变量与函数值的取值范围和变化趋势,然后根据函数图象直观感受函数增减性,最后在实际问题中应用增减性研究函数的取值范围或最值。
2.教学起点
根据班级学生生情,适时在平面直角坐标系下,补充“x<a,x=a,x>a”,“y<b,y=b,y>b”对平面的划分。在进行教学实践时,笔者发现,学生普遍对“已知函数值的取值范围,求自变量的取值范围”即从x轴对应图象找到y轴的相应区域存在困难,从y轴对应图象找到x轴的相应区域亦如此;对平行于y轴的直线“x=a”,平行于x轴的直线“y=b”划分平面区域理解不深刻,导致从函数角度对解不等式“y>b”、“y<b”进行解释时图象找寻存在困难。可以根据不同生情,在前置课堂或本课引入中铺垫先行知识和观念。
会用待定系数法求二次函数的一般式和顶点式,理解从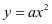 到
到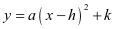 抛物线的平移规律,并能熟练得出抛物线的开口方向、对称轴、顶点,画出相应的示意图,根据函数图象直观解决实际问题。为学生适应高中数学教学要求,初中阶段二次函数基本能力应普遍要求学生掌握配方法将二次函数一般式化为顶点式,会求(给定自变量取值范围的)函数最值。
抛物线的平移规律,并能熟练得出抛物线的开口方向、对称轴、顶点,画出相应的示意图,根据函数图象直观解决实际问题。为学生适应高中数学教学要求,初中阶段二次函数基本能力应普遍要求学生掌握配方法将二次函数一般式化为顶点式,会求(给定自变量取值范围的)函数最值。
3.教学拓展
二次函数与一元二次方程的教学教材上主要考察了抛物线与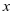 轴的交点(即函数值为0)的情况,根据班级具体学情,可以适时在以下几个方面拓展:
轴的交点(即函数值为0)的情况,根据班级具体学情,可以适时在以下几个方面拓展:
(1)方程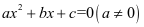 的解是二次函数
的解是二次函数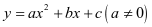 与
与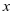 轴
轴
交点的横坐标。设两交点的坐标分别为 ,则有:
,则有:
①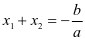 ,②
,②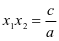 ,③
,③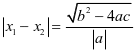 .
.
(4)抛物线与根与系数关系的结合。当抛物线与直线的交点难求时,保留根与系数的关系,转而设交点坐标。
【例题】已知直线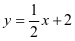 分别交x轴、y轴于A,B两点,抛物线
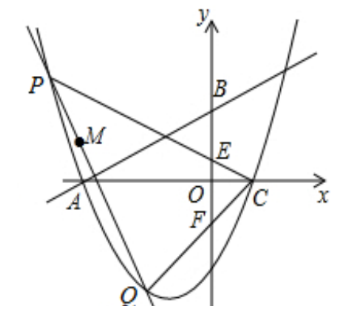
分别交x轴、y轴于A,B两点,抛物线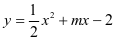 经过点A,和x轴的另一个交点为C. 如图,经过点M(-4,1)的直线交抛物线于点P,Q,连接CP,CQ分别交y轴于点E,F,求OE•OF的值[3].
经过点A,和x轴的另一个交点为C. 如图,经过点M(-4,1)的直线交抛物线于点P,Q,连接CP,CQ分别交y轴于点E,F,求OE•OF的值[3].
【分析】联立直线PQ和抛物线的解析式求解点P,Q坐标,发现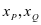 不好求,于是保留根与系数的关系
不好求,于是保留根与系数的关系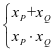 ,设点
,设点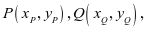 待定系数法求直线PC,QC解析式(含
待定系数法求直线PC,QC解析式(含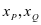 ),进而求得OE•OF是关于
),进而求得OE•OF是关于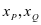 的表达式,整体代入求值即可。
的表达式,整体代入求值即可。
三、教学建议
关注数学核心知识的教学设计、实践与反思,注重学生的深度理解、成长与独立,笔者挖掘函数与方程教学的本质困难,总结思维层面的可操作的程序,形成易于学生迁移运用的方法[4],促进教学减负提质。在以上教学实践经验基础上,笔者提出以下教学建议:
首先,要发展学生数学核心素养,长效落实教学减负提质。重视课本新课内容的教学和课本习题的开发。在教学中应精选例题,教师备课时注意教学语言的精炼和数学思想的准确。突破教学难点,能够给学生程序化的思维和方便操作的通法。教师通过具体范例的演示,将教学经验可视化。
其次,要拓展学生数学阅读范围,提高学生理性思维能力。教师应针对教材和配套教参拓展内容,提出开放性的问题,给学生探索的时间和交流的空间。鼓励学有余力同学阅读数学家传记和数学史发展相关书籍。
最后,成人者必先立己。数学教师要提高自身数学文化,阅读相关书籍,关注新时代对数学学科育人价值的需求,而不仅仅局限于考试。应着眼于学生未来发展,引领高观点下的初中数学核心价值。
参考文献:
[1]中华人民共和国教育部制定,普通高中数学课程标准(2017年版) [M],北京:人民教育出版社,2018.
[2]中华人民共和国教育部制定,义务教育数学课程标准(2011年版) [M],北京:北京师范大学出版社,2012.
[3]彭天晏主编,思维新观察[M],长江少年儿童出版社,2012年6月第1版.
[4]吴亚萍,中小学数学教学课型研究[M],福建教育出版社,2014年10月第1版:33.
厦门市思明区教育科学“十三五”规划2020年立项微型课题“结构化视角下‘函数与方程’教学实践研究”(课题立项批准编号:W2020Z0072),阶段性成果。