匀变速运动规律的应用

匀变速运动规律的应用

钱茂莎

四川省贸易学校 625000

公式

v_t =v₀+ at_， (1)

s=v₀t+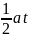², (2)

表明了匀变速运动的规律，从这两个公式我们还可以导出一个很有用的速度和位移的关系，从公式（1）解出t=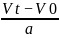 ,并把这个t值代入公式（2），就得到速度和位移的关系式：

v_t²- v₀²=2as （3）

当匀变速运动的初速度等于零时，上述三个公式就分别变成

v_t=at （4）

s=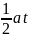² （5）

v_t²=2as （6）

上述公式可解有关物体运动的问题，用这些公式解题时需要注意各个物理量的正负符号，在代入各个物理量的数值时，这些数值都要用相应的单位来表示，通常我们是用国际单位制的单位来表示。

﹝例题1﹞某种飞机起飞时需要达到96米／秒的速度，起飞前在跑道上要匀速加速滑行20秒才能到达这个起飞速度，供这种飞机起飞的跑道至少要多长？

飞机在跑道上从静止开始做匀加速运动，初速度v₀=0，求出飞机在20秒内的位移s，就知道跑道至少要多长了。s可以用公式（5）求出，式中t是已知的，a是未知的，要求出a_n可以用公式（4），把已知t,v_t代入公式就得到a。

解：从公式（4）v_t=at得到

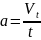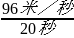= =4.8米／秒²，

代入公式（5）得到

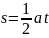²=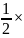 4.8米／秒² (20秒)²

=9.6 10²米。

答：跑道至少要960米长。

﹝例题2﹞一辆汽车以72千米／小时的速度行驶，司机看到交通红灯后立即刹车，汽车开始做匀减速运动，加速度的大小是2.5米／秒²。从刹车起，到汽车停下来位移是多大？

我们选汽车前进的方向为正方向，因此加速度取负值。v₀用米／秒作单位来表示：v₀=72千米／小时=20米／秒.因为汽车最后停下来，所以v_t=0.

要求出位移可以用公式（2），其中v₀,a是已知的，t是未知的。要求出t可以用公式（1），把v₀，v_t，a代入公式，就得到t。

解：从公式（1）v_t =v₀+ at得到

t=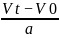

=

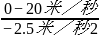
=8.0秒。

代入公式（2）得到

s=v₀t+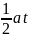²

=20米／秒 8.0秒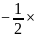 2.5米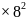／秒² 秒²

=80米

答：汽车的位移是80米。

这个例题也可以用公式（3）求解，把已知的v₀，v_t，a代入公式中，直接解出s即可。

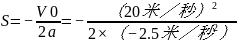
=80米

可见这个例题用公式（3）求解比较方便。

﹝例题3﹞一个滑雪的人，从89米长的山坡上匀加速滑下，初速度是1.5米／秒，末速度是3.5米／秒，他通过这段山路要用多长时间？

要求出t可以用公式（1）v_t =v₀+ at，式中v₀，v_t是已知的，a是未知的，a可以用公式（3）v_t²- v₀²=2as，由已知的v₀，v_t，s求出来，把求出来的a值代入公式（1）中就求出t.

这个例题并不要求算出a值，我们可以从公式（1）和（2）消去a,直接解出t,这样求解更方便。

解：v_t =v₀+ at

v_t²- v₀²=2as

由后一公式得到

a=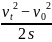

代入前一公式中，消去a,解出t:

t=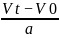

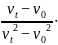= 2s

=

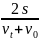
代入已知数值得到

t=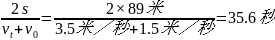

答：所用的时间是35.6秒。

这个例题最后导出的关系式t=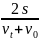 是有物理意义的，在匀变速直线运动中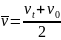， ，所以，t= 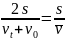表示在匀变速直线运动中所用时间等于位移除以平均速度。

从上面的例题可以看出，一个题目往往可以有不同的解法，我们应该在认真审题的基础上，选择比较简便的办法来求解。

比较复杂的题目，如例题2和3往往不能从已知量直接求出未知量。在这种情况下，可以分步来考虑，从未知量出发，考虑要求出这个未知量需要知道哪些别的物理量，而这些物理量中哪些是已知的，哪个是未知的；再考虑求出这个未知量又需要知道哪些物理量。这样考虑下去，直到需要知道的物理量都是已知量，再进行计算，就可以求出答案来。

最后计算答案时，可以像例题2那样分步计算，也可以象例题3那样，先进行文字运算，求出用已知量表达未知量的代数式，然后代入数值，直接算出答案。后一解法往往比较简便，同学们在熟悉分步计算的同时，可以逐步练习这种解题方法。