广西 桂林市火炬中学 541004
摘 要:专题从以下四个方面来论述:一、“双减”之下专题的知识点要专一,不要面面俱到。二、专题的例题要讲透,从而得出解法步骤。三、“双减”之下专题的变式要层层递进。四、“双减”之下专题的提升巩固要有梯度。
关键词:专题 、 专一 、 步骤、 变式、层层递进
中共中央办公厅、国务院办公厅《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》出台以来,这个学期准备上一节城区公开课,到底上一节什么课呢?上一节新课吗?上新课进度又难以确定,时间定不了。所以决定上一节专题课,也是初三了虽然是九年级上学期还没有到初三复习。现在刚刚上完反比例函数,一般是反比例函数与二次函数综合起来考的比较多,但是二次函数还没有学不能和二次函数综合起来出题。所以就想到一次函数和反比例函数的综合题。
一、“双减”之下专题的知识点要专一,不要面面俱到。
刚刚开始我是取一个“一次函数与反比例函数的综合题”课题。我从四个专题(四个类型)入手,类型一求反比例函数与正比例函数的交点坐标;类型二利用反比例函数和一次函数的图像求不等式的解集;类型三求一次函数与反比例函数图像围成的三角形的面积。类型四求函数表达式及交点的坐标。经过一节课的磨课觉得知识点太多,面面俱到学生学得不透,达不到专题的效果。第二次磨课只要两个类型也就是两个专题,还是觉得知识点多了一点。最后决定只讲一个知识点。
类型一求反比例函数与正比例函数的交点坐标;解题思路求反比例函数的交点坐标的常规思路,将两个函数表达式联立成一个方程组,通过解方程组求得交点坐标。如果已知正比例函数与反比例函数的一个交点坐标,求另一个交点坐标时,常利用反比例函数的中心对称性,即利用“两个交点的纵坐标互为相反数,横坐标互为相反数。”快速求解。
例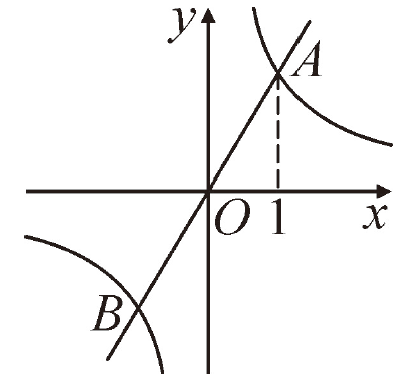 1、正比例函数
1、正比例函数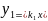
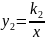 的图像
的图像相交于A, B两点,若点A
的坐标为(2,1),则点B
的坐标为()
A .(1,2) B.(-2,1)
C.(-1,-2) D.(-2,-1)
变式1
如图(2),直线y=kx(k>0)与
双曲线y= 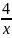 交于A(
交于A(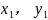 ),
),
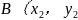
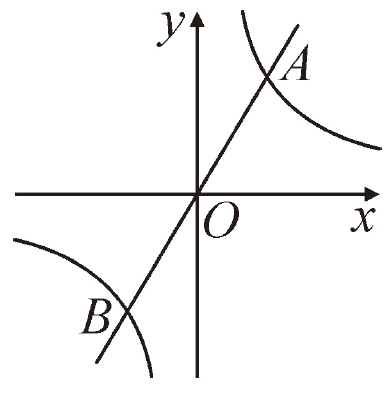 )两点,
)两点,
则 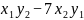 的值等于
的值等于
_____________________________.
分析:利用正比例函数与反比
例函数关于原点中心对称性讲
解例1,点A 的坐标为(2,1),
则点B的坐标为(-2,-1),关于原点对称横坐标的绝对值不变,只有符号改变了,变成了他们的相反数。变式1也是利用正比例函数与反比例函数关于原点中心对称性,
解: 2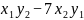
所以,就有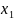 = -
= -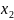 ,
,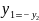
.因为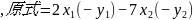
= - 2x4+7x4
=20
好多学生会恍然大悟,哦,原来是这样的。
解法二: 2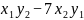
所以,就有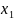 = -
= -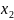 ,
,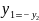
.因为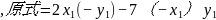
= - 2x4+7x4
=20
分析:A(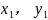 )
)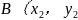 )两点都是双曲线y=
)两点都是双曲线y= 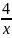 上的点,则
上的点,则 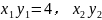 =4.所以就得上面的两种解法。还有其他的解法。不再一一列举。我觉得例1的变式1这题型很好, 也比较新颖很舍不得丢掉。最后决定只讲类型二利用反比例函数和一次函数的图像求不等式的解集。
=4.所以就得上面的两种解法。还有其他的解法。不再一一列举。我觉得例1的变式1这题型很好, 也比较新颖很舍不得丢掉。最后决定只讲类型二利用反比例函数和一次函数的图像求不等式的解集。
二、专题的例题要讲透,从而得出解法步骤。
例1如图,正比例函数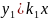 与反比例函数
与反比例函数
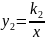
 的图像相交于 A,B两点,其中
的图像相交于 A,B两点,其中
点A的横坐标为1,当 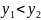 时,
时,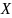 的
的
取值范围是( )
x<-1或 x>1 B.-11
C.-1
解题思路,解这类题要充分利用数形思想和转化结合思想。将求不等式的解集转化为比较反比例函数和一次函数的函数值的大小。当位于反比例图像位于一次函数的图像的下方时,反比例函数值小于一次函数值;当反比例函数在一次函数的图像的上方时,反比例函数值大于一次函数值。
从而得出解法,第一步先确定A,B两点的横坐标 ,这题
A点的横坐标是1,根据反比例函数图像关于原点成中心对称的性质。B点的横坐标是-1。
第二步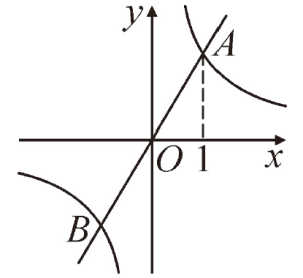
![]()
![]() 划分区域,确定哪
划分区域,确定哪
个区域是符合要求的即分别从
交点坐标A,B两点作垂线垂直x轴,
两条垂线和y轴把它们的图像分成
四个部分。哪个区域符合要求。这题
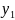 是正比例函数的图像是直线。
是正比例函数的图像是直线。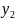 是
是
反比例函数的图像是曲线。从左向右数过去分成一、二、三、四个区域。第一个区域是直线在曲线下方的区域是符合要求的。和第三个区域也是直线在曲线下方的区域是符合要求的。第一个区域所对应的x的取值范围是x<-1;第三个区域所对应的x的取值范围是0
四这样间隔的,这是经验总结得的。这题如果用解不等式的形式解得出来吗?学生肯定回答解不出来,不知道A,B两点的坐标,求不出反比例函数与一次函数的解析式,所以直接解不等式求不出来解集的。我们用反比例函数与一次函数的图像就可以解得出不等式的解集。这就是我要学习的目的。
三、“双减”之下专题的变式要层层递进。
例如变式1:如图,一次函数y=x+4与反比
例函数 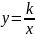 (x<0)的图像相交于 A,B
(x<0)的图像相交于 A,B
两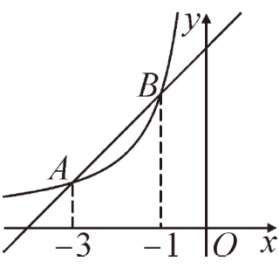 点,其横坐标为-3,-1,则关于
点,其横坐标为-3,-1,则关于
x的不等式 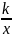
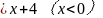 的解
的解
集为( )
X<-3 B.-3
C.-1
这一题变式1与例1相比是给出不等式 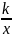
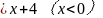 ,不是
,不是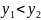 ,有的学生就不知道把它变成
,有的学生就不知道把它变成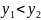 的形式。虽然这题可以算出A,B两点的坐标,也可以求得出反比例函数的解析式,也可以利用解不等式的形式解出来。用反比例函数与一次函数的图像就可以解得出不等式的解集。这题x的取值范围是
的形式。虽然这题可以算出A,B两点的坐标,也可以求得出反比例函数的解析式,也可以利用解不等式的形式解出来。用反比例函数与一次函数的图像就可以解得出不等式的解集。这题x的取值范围是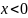 ,只有在第一象限内符合要求,只有三个区域,
,只有在第一象限内符合要求,只有三个区域, 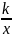
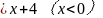 直线在上方,曲线在下方只有第二个区域是符合要求的。所以x的取值范围是 B.-3
直线在上方,曲线在下方只有第二个区域是符合要求的。所以x的取值范围是 B.-3
求得出反比例函数的解析式,也可以利用解不等式的形式解出解集简单。还是用反比例函数与一次函数的图像就可以解得出不等式的解集简单。这是学生一定会说用反比例函数与一次函数的图像就可以解得出不等式的解集简单,我们也达到了学习利用反比例函数和一次函数的图像求不等式的解集这个知识点。达到数学简便的思想。
变式2:直线y=kx+b与反比例函数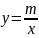 的图像
的图像
相交于点A,B,期中点A的坐标为(-2,4),
点B的横坐标为4,则不等式
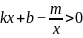 的解集为________________.
的解集为________________.
这题和上面两题有所区别,没有图像要让学生自己把图形画出来,有的学生就不知道怎么画,到底在哪几个象限?一个从A的坐标为(-2,4)在第二象限,直线y=kx+b与反比例函数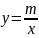 的图像相交于点
的图像相交于点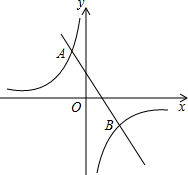 A,B,期中点A的坐标为(-2,4),
A,B,期中点A的坐标为(-2,4),
点B的横坐标为4,所以他们的图像
一定在二、四象限。把草图画出来,
不等式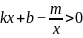 的解集化
的解集化
为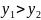 的形式去做就好做多了。
的形式去做就好做多了。
A,B点横坐标确定了,一个是 -2,一个
是4。
四、“双减”之下专题的提升巩固要有梯度。
有基础题和提升题和拓展题。给成绩一般的做达到巩固知识的目的,也要有提升题给中等的学生做达到能力提升的效果。拓展题拓展学生的思维能力以及视野。
总之,专题知识点要专一,讲清讲透,让学生理解并能灵活运用。以及拓展学生的思维能力和视野。