1 国网重庆市电力公司电力科学研究院 重庆 401123; 2 西南大学工程技术学院 重庆 400715
摘要:本文在确定型多源联合优化调度模型中引入需求响应机制,将负荷划分为居民负荷和工业负荷两大类,针对居民负荷和工业负荷的不同特性,分别建立了考虑用户参与度度的需求响应模型和工业负荷价格型需求响应模型,提出了一种考虑不同负荷类型的新型电网源荷协调优化调度策略,给出了模型目标函数和约束条件的数学表达式。最后,通过改进的IEEE39节点系统算例验证了该策略的有效性和适用性。
关键词:新型电网;居民负荷;工业负荷;负荷类型;源荷协调;优化调度
致谢:感谢国网重庆市电力公司电力科学研究院项目提供支持。
0 引言
随着高比例、大规模可再生能源发电并网,多源并存的新型电网格局呈现,对电力系统的适应性提出了更高的要求和挑战的同时,也为新型电网的优化协调调度奠定了夯实的现实基础。风电起步最早、应用最广,现有的优化调度研究多为风火、风水火联合调度策略[1-3]。现阶段引入的负荷侧需求响应模型多为价格型需求响应模型,且模型简单粗放,未能根据不同类型的负荷特点建立精细化的需求响应模型从而充分挖掘和利用需求响应的灵活性。
为此,本文在多源联合调度模型的基础上,将负荷划分为居民负荷和工业负荷两大类,针对居民负荷和工业负荷的不同特性,分别建立考虑用户参与度的居民负荷需求响应模型和工业负荷价格型需求响应模型,提出一种考虑不同负荷类型的源荷协调优化调度策略。最后,通过改进的IEEE39节点系统算例验证了该策略的有效性和适用性。
1 新型电网源侧联合调度模型
1.1 含光热电站的新型电网能量转换特性
典型的含光热电站的新型电网主要结构及能量流动,主要由光场(Solar Field,SF)、储热系统(Thermal Energy Storage System,TESS)和发电系统(Power Block,PB)三部分构成,通过传热流体(Heat Transfer Fluid,HTF)实现能量在各部分之间的传递。SF将直射太阳光辐射汇聚到集热装置,将太阳能转换为热能传递到传热流体,一部分热能随着传热流体输送到PB,产生热蒸汽做功驱动汽轮机发电,实现热-电转换,另一部分热能随着传热流体储存至TESS,根据调度要求放热发电,实现能量时移。
内部的功率平衡如下:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
式中,PSF t为t时段光场的直射太阳光辐射量PS t转化后的热功率;PPD t为t时段传热流体输送到发电系统的热功率;Pcha t、Pdis t分别为t时刻储热系统的储热、放热功率;PCSP t为t时段光热电站输出的电功率;ηs-th为集热装置的光-热转换效率;ηth-p为发电系统的热-电转换效率。
TESS的工作状态与储热容量、储/放热功率和当前的储热水平有关,能量方程如下:
![]() (4)
(4)
![]() (5)
(5)
![]() (6)
(6)
![]() (7)
(7)
式中,ETESS t为t时段TESS内存储热能;ETESS min为防止储热熔盐凝固TESS最小储热量,ETESS max为防止储热熔盐过热TESS最大储热量,通常TESS在一个调度周期内的始末储热量应相等;xstorage t为t时段TESS的储放热状态,为0-1变量,1表示TESS存储热能,0表示TESS释放热能;Pcha max、Edis max分别为TESS最大储热、放热功率;γ为TESS热量耗散系数;ηcha、ηdis分别为TESS储热、放热效率。
PB的热力循环系统类似于火电,也存在出力上下限、爬坡能力上下限和最小开停机时间:
![]() (8)
(8)
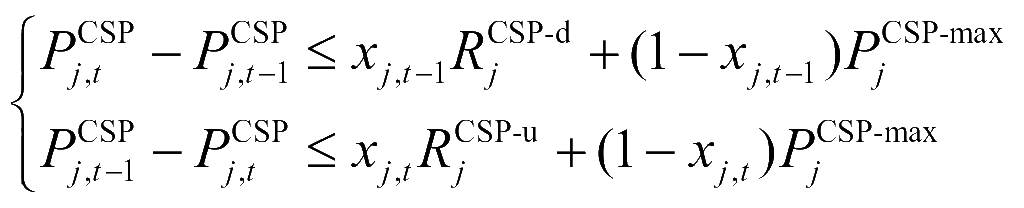 (9)
(9)
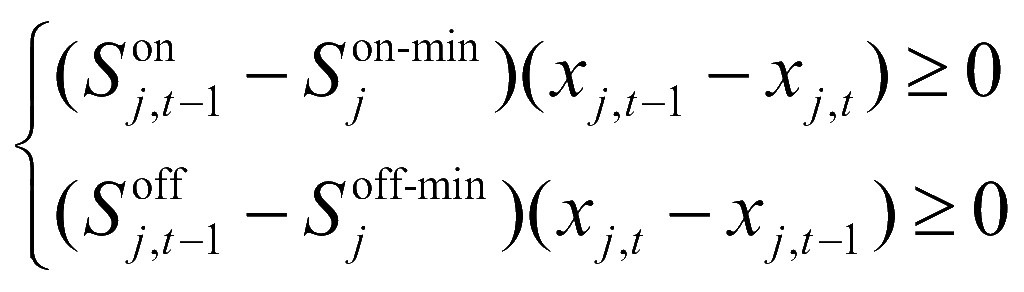 (10)
(10)
式中,xj,t为CSPP机组j在时段t的启停状态,为0-1变量;PCSP-max j、PCSP-min j分别为CSPP机组j的最大、最小出力值;PCSP-u j、PCSP-d j分别为CSPP机组j的向上、向下爬坡速率;Son j,t-1、Soff j,t-1分别为CSPP机组j到t-1时刻已持续的开机、停机时间;Son-min j,t、Soff-min j,t分别CSPP机组j的最小持续开机、停机时间。
1.2 目标函数
多源联合确定性调度模型中包含常规火电、风电和CSPP,综合考虑常规机组的燃料成本、常规机组和CSPP机组的启停成本,以系统的总调度成本最低为目标函数进行优化调度:
![]() (11)
(11)
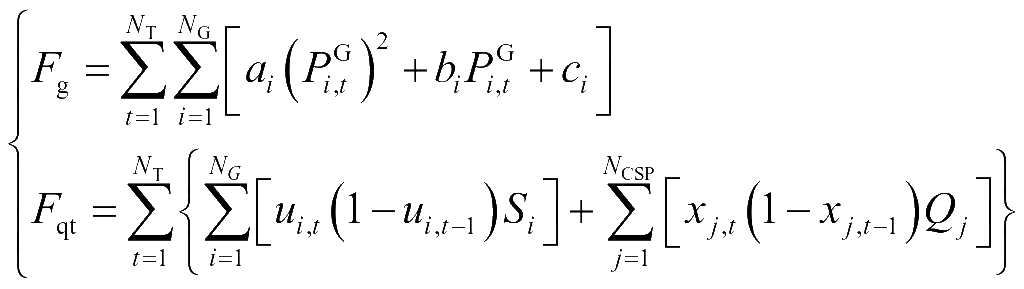 (12)
(12)
式中,Fg为常规机组的燃料成本,Fqt为常规机组和CSPP机组的启停成本;NT、NG、NCSP分别为调度时段数、常规机组台数、CSPP机组台数;PG i,t为t时段常规机组i的出力;ai、bi、ci均为常规机组i的成本系数;Si、Qj分别为常规机组i、CSPP机组j的启停成本;ui,t、xj,t分别为常规机组i、CSPP机组j在时段t的启停状态,均为0-1变量。
2 计及不同负荷类型的源荷优化调度模型
2.1 考虑用户参与度的居民负荷需求响应模型
针对居民负荷容量小、地理位置分散,独立性强,相互之间难以协调等问题,通过居民负荷聚合商 (Residential Load Aggregator, RLA)增加可转移负荷可以获得居民负荷的正需求响应(Positive Demand Response, PDR),通过RLA减少可转移负荷可以获得居民负荷的负需求响应(Negitive Demand Response, NDR)。本文在模型中引入用户参与度来表征居民负荷DR的变化,通过以下方式估算RLA提交的DR容量的实际可用情况:
![]() (18)
(18)
![]() (19)
(19)
式中,![]() 、
、![]() 分别为RLA可以提供的最大正需求响应容量和最大负需求响应容量;
分别为RLA可以提供的最大正需求响应容量和最大负需求响应容量;![]() 为RLA聚合的居民用户的数量;
为RLA聚合的居民用户的数量;![]() 、
、![]() 分别为RLA聚合的每个居民用户可以提供的最大正需求响应、负需求响应的平均值;
分别为RLA聚合的每个居民用户可以提供的最大正需求响应、负需求响应的平均值;![]() 、
、![]() 分别为RLA正需求响应和负需求响应的用户参与度,取值均在[0,1]区间内,
分别为RLA正需求响应和负需求响应的用户参与度,取值均在[0,1]区间内,![]() 意味着RLA提交的可用DR容量均实际可用,
意味着RLA提交的可用DR容量均实际可用,![]() 意味着RLA提交的可用DR容量均不实际可用,其具体取值可以通过综合行为分析和大数据挖掘等方法来确定。
意味着RLA提交的可用DR容量均不实际可用,其具体取值可以通过综合行为分析和大数据挖掘等方法来确定。
RLA正需求响应和负需求响应均不可超过最大可用DR容量,并且正需求响应和负需求响应不能同激活。此外,为不影响用户用电的体验,保证用户电力消费的满意度,整个调度周期激活的总正需求响应和总负需求响应能量不能大于事先约定的最大值,并且需求响应前后居民负荷的值应保持不变。这些约束可以表示为:
![]() (20)
(20)
![]() (21)
(21)
![]() (22)
(22)
![]() (23)
(23)
![]() (24)
(24)
式中,![]() 、
、![]() 分别为t调度时段的RLA正需求响应和负需求响应功率;
分别为t调度时段的RLA正需求响应和负需求响应功率;![]() 为0-1变量,表示RLA需求响应的激活状态,1表示激活了RLA正需求响应,0表示激活了RLA负需求响应。
为0-1变量,表示RLA需求响应的激活状态,1表示激活了RLA正需求响应,0表示激活了RLA负需求响应。![]() 、
、![]() 分别为调度周期的总正需求响应最大值和总负需求响应的最大值。
分别为调度周期的总正需求响应最大值和总负需求响应的最大值。
RLA的正、负需求响应均会得到激励补偿,而不可转移负荷则以电力时长实时电价进行结算。因此,RLA在需求响应后的电费总支出为:
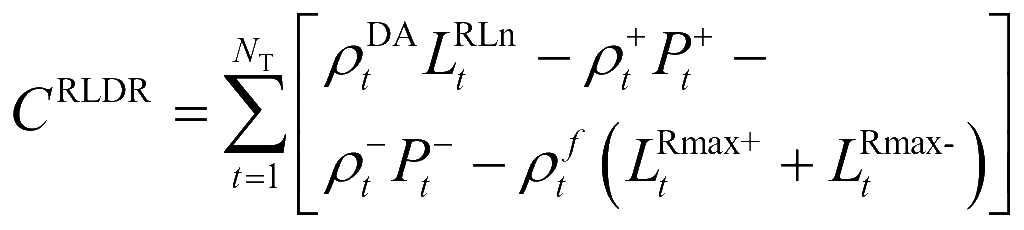 (25)
(25)
式中,![]() 为调度时段t的不可转移负荷;
为调度时段t的不可转移负荷;![]() 、
、![]() 分别RLA正需求响应、负需求响应的激励费用;
分别RLA正需求响应、负需求响应的激励费用;![]() 为进行RLA需求响应的固定费用。
为进行RLA需求响应的固定费用。
2.2 工业负荷的价格型需求响应模型
工业负荷的价格型需求响应模型如下所示:
![]() (26)
(26)
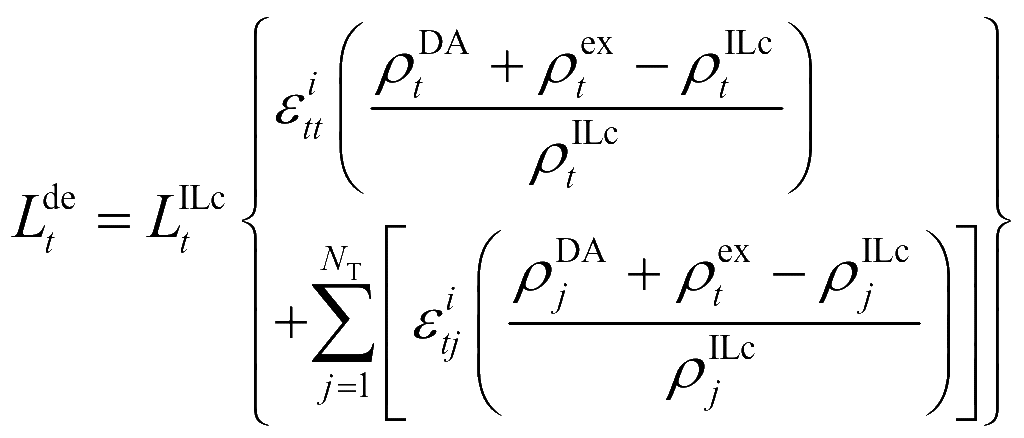 (27)
(27)
![]() (28)
(28)
式中,![]() 为调度时段t的总工业负荷;
为调度时段t的总工业负荷;![]() 、
、![]() 分别为调度时段t的工业基荷和电价需求响应引起的工业负荷偏差量,其中工业基础负荷可以通过工业负荷历史数据或工业用户的中长期生产计划得到,工业负荷偏差量则由电量电价弹性系数模型求解得到;
分别为调度时段t的工业基荷和电价需求响应引起的工业负荷偏差量,其中工业基础负荷可以通过工业负荷历史数据或工业用户的中长期生产计划得到,工业负荷偏差量则由电量电价弹性系数模型求解得到;![]() 为工业用户事先签订的合同约定的基础电价;
为工业用户事先签订的合同约定的基础电价;![]() 为工业用户削减/增加负荷产生的的额外费用。在整个调度周期内,需求响应前后的工业负荷总量相同。
为工业用户削减/增加负荷产生的的额外费用。在整个调度周期内,需求响应前后的工业负荷总量相同。
工业负荷价格型需求响应后的电费支出为:
![]() (29)
(29)
另外,由于工业负荷主要为钢铁冶炼厂等连续性的工业过程,根据工业实际,模型还应包含如下约束:
![]() (30)
(30)
![]() (31)
(31)
![]() (32)
(32)
![]() (33)
(33)
![]() (34)
(34)
式中,![]() 、
、![]() 分别为工业负荷最大值和最小值;
分别为工业负荷最大值和最小值;![]() 、
、![]() 分别为工业负荷爬坡速率上下限;
分别为工业负荷爬坡速率上下限;![]() 为0-1变量,表示电弧炉(Electric arc furnace, EAF)等装置的开停机状态,1表示开机,0表示停机;
为0-1变量,表示电弧炉(Electric arc furnace, EAF)等装置的开停机状态,1表示开机,0表示停机;![]() 、
、![]() 均为EAF变量,为1表示EAF启动/关机,否则为0;
均为EAF变量,为1表示EAF启动/关机,否则为0;![]() 、
、![]() 分别为工业负荷的最大持续开机时间和最小持续停机时间。
分别为工业负荷的最大持续开机时间和最小持续停机时间。
2.3 计及不同负荷类型的源荷优化调度模型目标函数及约束条件
计及不同负荷特性的源荷协调优化调度模型仍以系统的总调度成本最低为目标函数进行优化调度。总调度成本综合考虑常规机组的燃料成本、常规机组和光热电站的启停成本,数学表达式参见公式(11)~(12)。
常规机组和光热电站机组运行约束、电站内部功率平衡约束以及TESS运行约束在前文有详细说明,故在此不再赘述,具体参见公式(1)~(10)和公式(13)~(17)。
3 算例分析
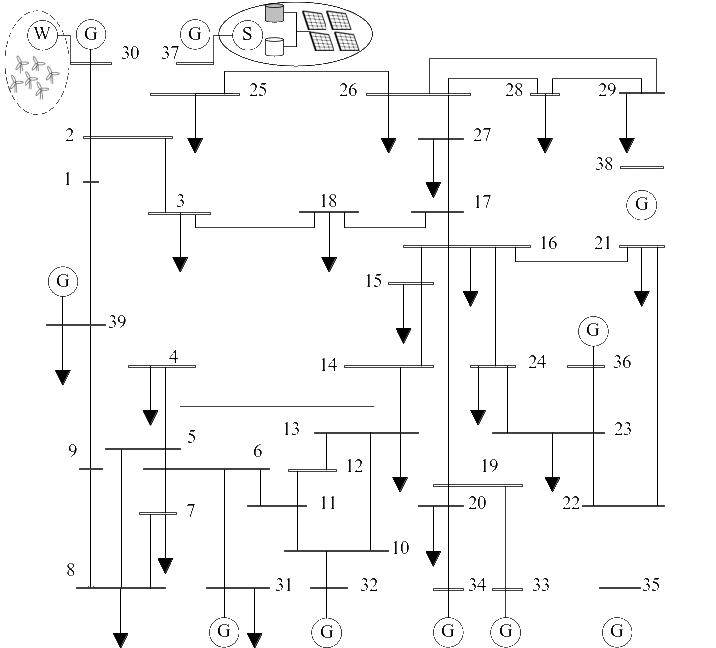
图1 改进的IEEE 39节点系统接线图
Fig. 1 Diagram of Modified IEEE 39-bus power system
图1所示,建立改进的含CSPP的IEEE39节点系统[4],系统包含10台火电机组、一个100MW光热电站和一个400MW风电场,初始储热容量为200MW。将RDR和IL-PBDR分别作为两个整体进行分析。需求响应前后的负荷曲线和工业负荷PBDR的各时段电价分别如图2和图3所示。
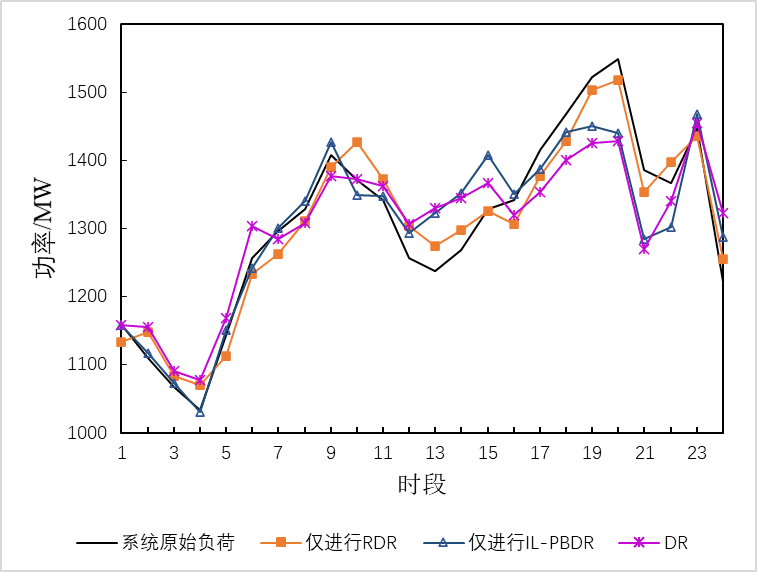
图2需求响应前后负荷曲线
Fig. 2 Load curves before and after DR
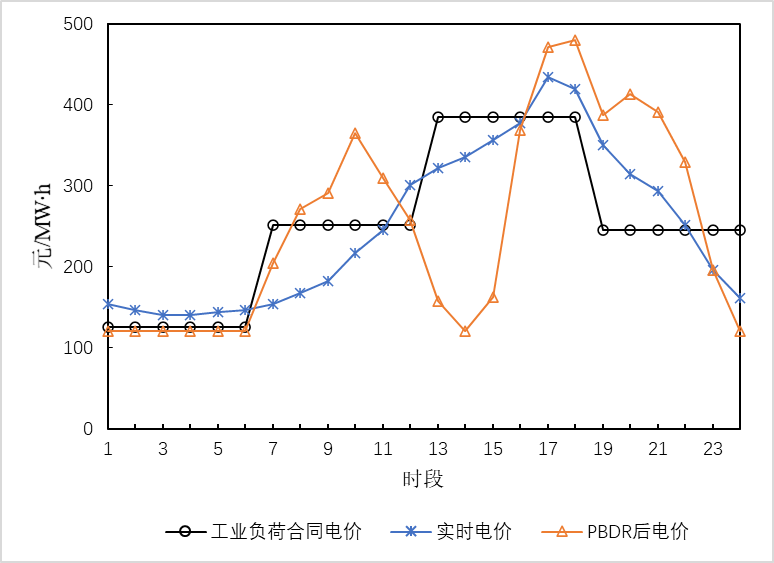
图3工业负荷PBDR的各时段电价
Fig. 3 The electrical price of Industrial Load PBDR
从图2和图3中可以看出,无论是RDR还是IL-PBDR都明显改变了需求侧用户的电力消费习惯,较之系统原始负荷,起到了削峰填谷的作用。其中,IL-PBDR通过对电价的响应实现负荷的转移,使得负荷峰值下降了81.13MW,谷值上升了2.5MW,峰谷比由系统原始负荷的1.5降为1.41;在仅进行RDR后,负荷峰值也下降了30.4MW,谷值上升了36.8MW,峰谷比由系统原始负荷的1.5降为1.42。而在当引入DR(即同时进行RDR和IL-PBDR)后,负荷峰值下降了93.68MW,谷值上升了44.35MW,峰谷比由系统原始负荷的1.5降为1.35,负荷曲线取得了更为显著的削峰填谷的效果。因此可以得出,单独的RDR和IL-PBDR都能起到平滑负荷曲线的效果,并且两者同时作用可以相互促进削峰填谷的效果,即RDR与 IL-PBDR具有良好的协同效应,引入DR(即同时进行RDR和IL-PBDR)后能最大程度平滑负荷曲线。引入DR后,RDR和IL-PBDR在各时段的需求响应参与量如图4所示。
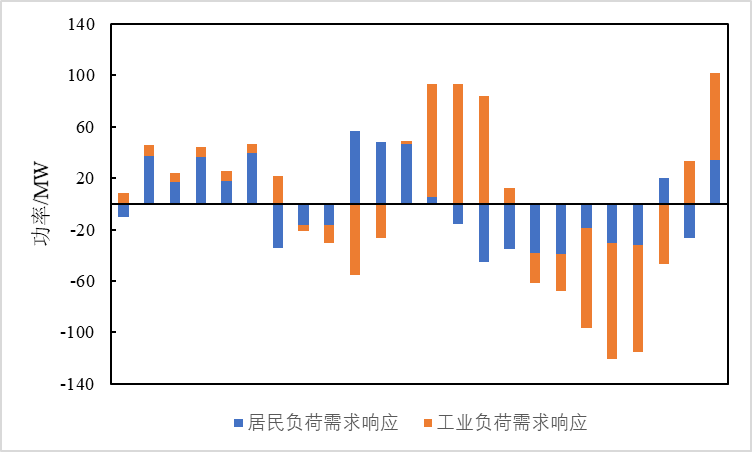
图4引入DR后RDR和IL-PBDR各时段的响应量
Fig. 4 The participation power of RDR and IL-PBDR
表1是否计及需求响应的经济调度结果对比
Table 1 Optimization results comparison between dispatching strategy with and without Demand Response
模型 | 总调度成本/元 | 启停成本/元 | 燃料成本/元 |
无DR | 533060 | 40000 | 493060 |
只计及RDR | 521460 | 32800 | 488660 |
只计及IL-PBDR | 514830 | 29400 | 485430 |
计及RDR和IL-PBDR | 511740 | 23000 | 488740 |
为进一步分析需求响应对含储热光热电站电力系统经济调度的效用,分别对无DR、只计及RDR、只计及IL-PBDR、计及RDR和IL-PBDR(即本文建立的模型)的经济调度模型进行求解,结果统计在表1中。从表1中可知,在负荷侧引入需求响应机制显著降低了系统的总调度成本,其中,同时计及RDR和IL-PBDR时,系统的总调度成本最低,经济性达到最优。
4 结论
本文主要得出如下结论:
1)在负荷侧引入DR后一方面可以减少机组的启停,降低机组的启停成本,一方面可以适应风电的反调峰特性,促进可再生能源的消纳,降低机组的燃料成本,从而降低系统的总调度成本。其中,同时计及居民负荷和工业负荷特性时,系统的总调度成本最低,经济性达到最优。
2)居民用户的电力消费情况受各种因素(如假期,天气条件等)的影响,为估算RLA提交的DR容量的实际可用情况而在RLA需求响应模型中引入的用户参与度的取值对模型的影响很小,建立的计及需求响应的调度模型的普适性较强。制定的调度策略具有一定优越性,可为含光热电站的新型电网源荷协调运行研究提供参考。
参考文献
崔杨, 周敏涛, 严干贵, 等. 考虑环境成本及网络约束的风-火联合发电调度[J]. 电网技术, 2017, 41(11): 3457-3462
马丽叶, 王志强, 陆肖宇, 等. 基于机会约束规划的风–火–蓄联合系统优化调度[J]. 电网技术, 2019(9).
张翔宇, 李丹, 张予燮,等. 考虑N-1安全约束的风-火-蓄联合优化调度模型及仿真[J]. 水电能源科学, 2019(8):202-206.
Kandasamy N K, Tseng K J, Boon-Hee S. Virtual storage capacity using demand response management to overcome intermittency of solar PV generation[J]. IET Renewable Power Generation, 2017, 11(14): 1741-1748.