安徽省庐江中学 231500
摘要:数学在接受高中教育的过程中起着非常重要的作用。因此,在高中数学课堂教学中培养和提高学生解决问题的能力,可以有效地提高学生的数学成绩,以及学生的问题分析能力、解决问题的能力和思维逻辑能力,对学生的学习和健康成长起着非常重要的作用。对学生来说,数学知识本身是非常合乎逻辑和抽象的,在学习过程中很容易产生一种排斥和阻力。在此基础上,本文对高中数学课堂教学中培养学生解决问题能力的方法和策略进行了深入的分析和研究。
关键词:高中数学;学生解题能力;培养方法与策略
前言:尽管在新课程的背景下,考试导向教育对高中数学教学的影响仍然存在,但在教学目标、教学模式和人员培训方向上都发生了很大的变化。素质教育要求我们的教学不应局限于学生对数学知识的掌握,而数学的应用并不是人才培养的最终目标。通过对新课程改革思想的不断解读,我认为高中数学教学应该以学生的长期发展为目标,培养数学解决问题的能力不仅仅是运用公式和解决问题的常规,而是培养和应用学生的综合数学能力,如推理能力、归纳法、总结能力、计算能力、合作能力、探究能力和创新能力。因此,在教学中,教师应重视教学方法的创新和改进,有效地提高学生的数学问题解决能力。
一、注重培养学生解题思维的多样化
在当前实际高中数学课堂教学中,教师应该在完整讲解教学内容后,应注意在该教材结构中能够全面设置重点知识,并尽量能及时向学生进行充分、系统地展示与详细具体的教学梳理过程,并最好能紧密将这些知识要点联系结合在一起,从而可以更好地来帮助学生自己构建一个完整、合理的知识网络。同时,教师还可以要求学生充分利用各种方法和思维来完成课堂作业,学生可以相互讨论和交流。这种方法不仅可以把课堂还给学生,还可以锻炼学生的多元思维。
例1:已知定义在 上的函数
上的函数 满足以下的三个条件:
满足以下的三个条件:
1.针对任意的 都有
都有 ;
;
2.针对任意的 ,都有
,都有 ;
;
3. 的图像关于
的图像关于 轴对称。
轴对称。
则,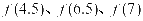 三者之间的存在怎样的大小关系?
三者之间的存在怎样的大小关系?
解析:这个问题不能仅仅用函数相关的知识来解决。因此,学生在解决这个问题时应该使用数字轴。学生在实际问题解决中能有效地将数轴和函数结合起来,生成相应的函数图像,通过分析得到: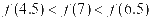 。在这个过程中,学生在解决问题的过程中不受函数知识的约束。它们将数轴与函数紧密结合,充分体现了学生解决问题的多样化思维。
。在这个过程中,学生在解决问题的过程中不受函数知识的约束。它们将数轴与函数紧密结合,充分体现了学生解决问题的多样化思维。
二、鼓励学生解题思维的发散
在新课程改革的背景下,应该鼓励学生独立探索和思考。在实际教学中,教师还应鼓励学生在解决问题的过程中尝试使用不同的解决方案,从而实现对一个问题的多种解决方案,找到不同的解决方案。
例2:已知复数 的模为2,求
的模为2,求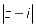 的最大值,可以使用以下三种解题方法:
的最大值,可以使用以下三种解题方法:
1.几何法
因为 ,所以点
,所以点 是圆
是圆 上的点,
上的点, 表示
表示 与
与 相对应的点之间的距离,如右图所示,能够获得当
相对应的点之间的距离,如右图所示,能够获得当 时,
时, 。
。
2.三角法
假设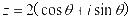 ,则
,则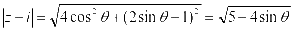 ,所以,当
,所以,当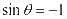 的时候,
的时候, 。
。
3.代数法
假设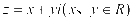 ,则
,则 ,
,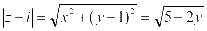 ,因为
,因为 ,当
,当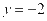 的时候,
的时候, 。
。
三、重视审题教学中对学生解题能力的培养
为了切实的培养学生数学综合能力,加强对学生解决实践问题能力的培养和提高是这过程中一个比较重要的前提和基础。在教学中,教师应该训练学生审题,而不是让学生回答问题,而是让学生找出问题中应该得到的信息,并将它们联系起来。在这个过程中,学生不仅可以提高他们发现关键词的能力,还可以提高他们检查问题的能力。
例3:已知抛物线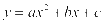 的对称轴是
的对称轴是 ,在
,在 轴上选取一段线段长为4,并且与过点
轴上选取一段线段长为4,并且与过点 的直线相交于点
的直线相交于点 ,求抛物线和直线的解析表达式。
,求抛物线和直线的解析表达式。
分析:结合本问题的要求,对已知条件进行有效变换,将变换后的条件进行组合,得到隐含信息:
由 为抛物线的对称轴,能够得出:
为抛物线的对称轴,能够得出: ,
,
由线段长为4能够得出: ,并且由抛物线经过点
,并且由抛物线经过点 ,能够得出:
,能够得出: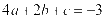 。
。
结合这三个等式进行求解之后能够得出: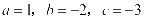 。
。
假设直线的表达式为: ,由于直线过点
,由于直线过点 和点
和点 ,就能够得出等式:
,就能够得出等式: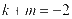 ,
, 成立,求解之后能够得出
成立,求解之后能够得出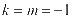 。
。
综上所述,抛物线的解析式为: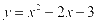 ,直线的解析式为:
,直线的解析式为: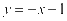 。
。
通过这个例子可以充分说明,标题中描述的内容经过上述转换后,问题可以很容易解决。
四、在概念理解中加强学生解题能力的培养
在培养和提高学生解决问题能力的过程中,教师应纠正学生对数学概念在数学学习中不重要的误解,并在实际课堂教学中设计用数学概念解决问题的练习。如果教师不逐步使用实际的数学知识,他们应该使用相应的数学概念来解决问题。
例4:复数 ,
, ,如果
,如果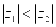 ,则实数
,则实数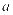 的取值范围是()。
的取值范围是()。
A.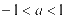 B.
B.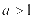 C.
C.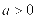 D.
D.
教师应引导学生在解题过程中正确使用复数的定义来解决问题,然后才能得到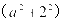 的平方根小于5的平方根,然后可以很容易地用这个定义来得到答案,所以选择一个A。
的平方根小于5的平方根,然后可以很容易地用这个定义来得到答案,所以选择一个A。
结语:总之,在高中数学教学中,提高和培养学生解决问题的能力不仅是当前新课程改革的重要要求,也是当前素质教育的重要要求。在注重培养思维和培养提高学生快速解决简单问题能力培养的教育过程中,也可以提高学生应用数学知识、掌握和理解相关数学知识的能力。因此,加强学校对当代高中生数学问题探究解决分析能力等的教育培养工作和教学提升都是非常之重要意义的。教师应在课堂教学中运用更具特色的教学方法和手段,更好地将问题解决的概念渗透到学生的实际学习中,注重学生问题解决方法的培养,只有这样才能更有效地提高学生的能力,学会解决问题。
参考文献:
[1]杨孝斌,吕传汉,吴万辉,袁景涛,李时建,卢焱尧.高中数学“一题一课多解变式”教学模式的理论构建与实践探索[J].中小学课堂教学研究,2021(11):14-19.
[2]舒华瑛.高中数学解题教学中学生高阶思维能力的培养——以恒成立求参数问题为例[J].延边教育学院学报,2021,35(05):205-209+214.
[3]于祥.“心有灵犀一点通”——浅析高中数学解题中常用的四大数学思想[J].数学学习与研究,2021(29):132-133.