齿轮箱主轴的静强度有限元分析

刘志龙

邦飞利传动设备 (上海 )有限公司，上海 200000

摘要：本文研究的对象是工程机械领域广泛应用的挖掘机用行走齿轮箱，行走齿轮箱的最大承载力集中在主轴上，将挖掘机的吨位参数转化为齿轮箱主轴受力约束条件，然后进行静强度有限元计算可以更准确的控制齿轮箱主轴的尺寸，在保证可靠性的同时让整个齿轮箱重量更轻。

关键词：齿轮箱 主轴 静强度计算 有限元分析

0引言 随着工程机械领域挖掘机市场竞争的日益激烈，挖掘机的机型升级换代明显加快，近年来，大吨位挖掘机的主要零部件如行走齿轮箱等开始逐步国产化，以前基本全部依靠进口，出于成本的压力开始采用国产齿轮箱作为替代产品，主机厂希望通过保质降本目的，打造出“网红”机型增加市场占有率。作为挖掘机重要的组成部分——行走齿轮箱在其中起着重要的关键作用，行走齿轮箱是挖掘机行走和提供径向支撑力的主要部件，而在齿轮箱中主轴是承载径向力及轴向力的主要零件，也是整个齿轮箱中成本较高的零件之一，为了提高机械性能，材料一般以锻造工艺为主。

国内目前在大吨位齿轮箱国产化方面自主设计的经验相对较少，更多的经验是在小型挖掘机上，以往的设计理念是由于对成本的控制没有过于严苛的要求，并且挖掘机工况相对比较复杂，行业内一般没有载荷谱，因此主机客户无法给出准确承载数据，为了保证承载能力满足使用要求，通常会粗略的计算并给予很高的安全系数，保证产品不会过载和失效。

然而随着对齿轮箱成本控制的提高和对承载力的更高要求，粗略计算显然已经无法满足使用需求，本文意在通过对挖掘机承载能力的分析给出齿轮箱受力边界条件并进行有限元分析，为了保证有限元计算的准确性，分析时加入了与主轴相关连零件，如齿圈、轴承座、轴承等。

1.几何模型建立

1.1有限元分析中使用的坐标系

本文中使用的坐标系如图1-1所示：

1.2有限元分析时使用的单位

表1 有限元分析中使用的单位

1.3材料参数

表2 材料参数

1.4几何模型

行走齿轮箱中的主轴是承载挖掘机径向支撑力的主要部件，并且是输入、输出扭矩的关键部件，还需要承受从轴承座传递来的驱动链轮作用力，受力情况较复杂，无法通过工程算法进行强度校核，一般采用有限元法进行强度校核。

齿轮箱通常由以下几部分组成：主轴、主轴承、轴承座、输出齿圈、浮动油封、一级行星轮系、二级行星轮系、三级行星轮系以及输入轴等。在计算主轴强度时，是将挖掘机链轮的作用力传递到主轴上的过程。

齿轮箱主轴的载荷传递原理如下：齿轮箱安装在挖掘机的行走链轮内，主轴的法兰面和挖掘机的机架相连接，齿轮箱输入端的动力源是液压马达，液压马达提供输出扭矩和转速，通过主轴功率流传递至两级或者三级行星轮系上，经过行星轮系降转速增扭矩，又将功率流传递至齿圈，齿圈与轴承座相连，齿圈的法兰面和挖掘机的链轮连接，再通过螺栓将齿圈法兰和链轮紧固，同时齿圈输出的扭矩传递至驱动链轮从而控制挖掘机的前进和后退。而驱动链轮在工作时，会将垂直方向的力作用在行走齿轮箱上，在齿轮箱法兰连接面形成一个垂直与齿圈圆柱面的径向力和一个弯矩，通过齿圈与轴承座传递至两个主轴承，再传递至主轴上。

在进行主轴静强度有限元分析时，需要保留轴承座、齿圈、两个主轴承作为载荷传递的载体，在有限元中对主轴、轴承座、齿圈、两个主轴承进行处理，将不影响分析结果的内齿以及其他特征如不重要的倒角、可忽略的小孔等删除，并将滚动轴承进行一体化处理，处理后进行有限元网格划分。

a 整体模型 b 主轴模型

图 1-2有限元模型

2.有限元网格划分及边界条件设置

主轴、轴承、轴承座和齿圈的有限元分析模型见图1-2。如图所示，整体使用3D Tetra 10单元划分网格，整体网格大小为10mm，局部应力较大的区域使用1～2mm的网格进行划分，以便获得更理想的分析结果。

主轴与两个轴承之间为摩擦接触，其余接触均为绑定接触。

2.1载荷和约束的施加

载荷施加：在对齿轮箱主轴进行静强度分析时，所考虑的载荷主要为驱动链轮给予的最大径向力和弯矩,以挖掘机带负载后总重70t为例,每台挖掘机有两台齿轮箱,因此可得到每台齿轮箱链轮所受的承载力Fr:

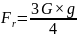
其中:

Fr:齿轮箱所受的径向力,单位N

G:挖掘机车重及负载总重,单位t

g:9.81m/s²

可得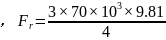 =515025 N

已知，齿圈与链轮连接螺栓孔分度圆直径D=450mm，链轮的径向力作用点距离齿圈法兰端面距离L=23mm，由平面任意力系的平衡方程，可将最大径向力Fr平移到齿圈的法兰面，得到平移后的径向力Fr和一个力偶M，

可得，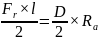

带入公式得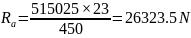 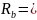， -26323.5 N

如图1-4所示，需要在齿轮箱法兰面上施加一个垂直于齿圈圆柱面的径向力F_r，并且通过在法兰面上施加一对力偶R_a、R_b来模拟弯矩。

约束施加：约束主轴法兰面螺栓孔的所有自由度，以及另一齿圈外圆柱接触面的五个自由度（释放绕轴线的旋转自由度）。

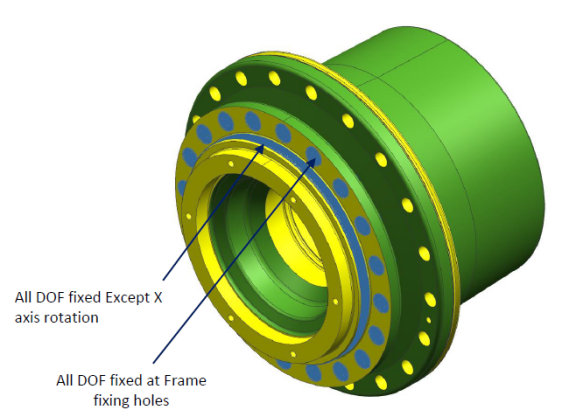
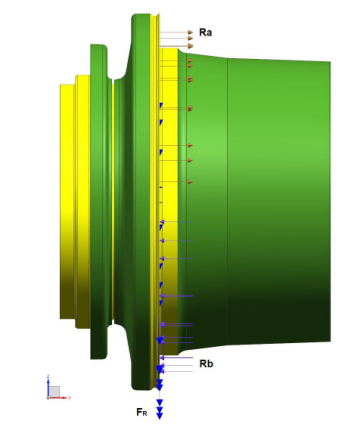
图 1-4边界条件设置

载荷大小如表3所示。

表3 边界载荷

3计算结果

判定结果：主轴的屈服强度为635MPa，当主轴应力大于635MPa时，静强度不满足要求。

3.1计算结果

由图2-1可知，主轴的最大应力为268MPa，其中最大应力点发生在主轴的大圆角处，次大应力点发生在轴承接触面的小圆角处，均小于许用应力，安全系数为2.37，满足静强度要求。主轴的最大变形为0.146mm，满足要求。

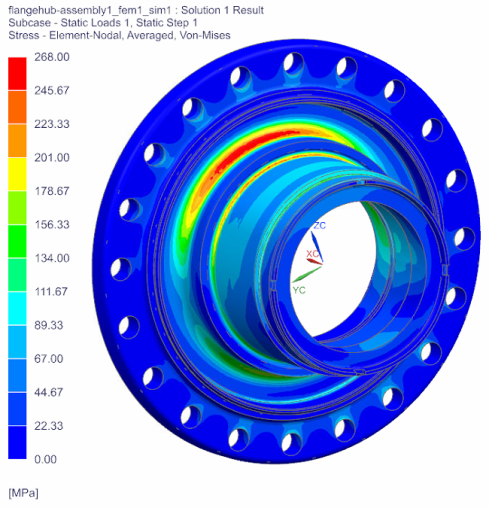
a. Von-Mises应力云图 b.变形云图

图2-1计算结果

3.2结果分析

通过计算结果及安全系数可知，该主轴结构满足使用要求，并且具有富余量。因此可以进一步对主轴进行优化设计，在强度富余量比较大的部位采用去除材料的方法降低零件的重量，经过优化后的主轴再次建模并施加边界条件后进行有限元分析，在保证安全系数要求的前提下可以得到更优的设计结构。

4结论

针对有限元计算不通过的情况：行走齿轮箱设计结构非常相似，通过有限元软件计算可以看出最大应力发生在主轴根部最大圆角处，因此在齿轮箱设计时可以通过优化主轴根部圆角来改善主轴强度的薄弱环节，此处圆角主要是为了作为轴承的挡肩使用，为了避免和轴承安装时产生干涉，可以通过增加过渡挡块，在挡块的内径上倒一个很大的倒角，这样可以保证主轴使用大圆角降低静强度校核不通过风险。

针对有限元计算结果通过，安全系数过高的情况：可以将结构上不起主要受力部位进行削减，再次进行有限元分析，根据分析结果进行优化设计，优化后的产品重量更轻并降低了材料成本。

齿轮箱主轴静强度分析的难点在于最大静载荷的确定，如很多进口齿轮箱制造企业，发展时间比较久，产品应用广泛并积累了大量的使用数据，在客户无法提供载荷谱时可以依靠主机的吨位等信息计算出一个相近载荷，用来进行设计计算校核使用，经过日积月累的使用经验计算出的结果具有一定的可靠性。但是国内更多的企业成立时间和外企相比普遍都很短，产品较新，没有丰富的实际使用经验，如果主机客户不提供载荷谱，在对齿轮箱主轴的受载情况进行分析时，如何在没有载荷谱的情况下确定挖掘机作用在齿轮箱上的负载尤为重要。本文提供了一种在没有提供使用工况载荷谱的情况下，通过挖掘机整机重量、链轮直径等参数与齿轮箱的结构尺寸，经过计算确定齿轮箱主轴受力情况，再根据计算工具有限元分析软件进行受力分析计算，从而得到满足使用要求的设计结构。

参考文献

1. [联邦德国]W.MERHOF E.M.HACKBARTH 韩雪梅 等译 履带车辆行驶力学 国防工业出版社

2. D.穆斯 H.维特 机械设计 （原书 第16版） 机械工业出版社

3. Forschungskuratorium Maschinenbau (FKM) ANALYTICAL STRENGTH ASSESSMENT

OF COMPONENTS 6th revised Edition, 2012

4