《平面向量》考点剖析

《平面向量》考点剖析

张培强

陕西省洋县中学  723300

一、 考情剖析

平面向量主要以平面几何、直角坐标系、三角函数等知识为基础，融合平面向量和解三角形两部分，对解决平面和空间中有关长度、角度、平行和垂直问题以及三角形问题具有优越性，因此在高考中占有重要的地位.高考试题热点集中在以下两个方面：

一是向量的基本运算、向量的平行、垂直的充要条件、图象的平移问题，大多以填空题、选择题出现，难度不大； 二是解答题，以向量知识为背景，与三角函数、数列、解析几何等知识相综合，一般为中档题。考查平面向量形成的知识网络交汇是命题趋势.

二、题型考点剖析

考点1：向量的线性运算

例1.设D为△ABC所在平面内一点，＝3，则

A.＝－＋  B.＝－  C.＝＋  D.＝－

【答案】A

【解析】：因为D为△ABC所在平面内一点，且＝3，

所以B，C，D三点共线，且D在BC的延长线上，如图：

(方法一)在△ABD中利用向量的加法：

＝＋＝＋＋＝＋＝＋(－)＝－＋.

(方法二)在△ACD中利用向量的加法：

＝＋＝＋＝＋(－)＝－＋.

(方法三)在△ABD中利用向量的减法：

＝－＝－＝(－)＋＝－＋.

方法点拨： 未知向量由已知向量来表示，要注意寻找未知向量与已知向量的联系，一

般要用到平行四边形法则、三角形法则、平行(共线)向量的性质以及平面向量基本定理．

考点2：共线定理的应用

例2.在△ABC中，N是AC上一点，且＝，P是BN上一点，若＝m＋，

则实数m的值为

【答案】

【解析】因为B，P，N三点在同一直线上，所以＝λ＋μ，λ＋μ＝1.

又＝m＋＝m＋×3＝m＋，所以m＋＝1, 所以m＝.

方法点拨：三点共线等价关系：A，B，P三点共线⇔＝λ(λ≠0) ⇔＝(1－t)·＋t(O为平面内异于A，B，P的任一点，t∈R) ⇔＝x·＋y·(O为平面内异于A，B，P的任一点，x∈R，y∈R，x＋y＝1)．

考点3.平面向量基本定理的应用

例3.如图，正方形ABCD中，M，N分别是BC，CD的中点，若＝λ＋μ，则λ＋μ＝(   )

A．2  B.   C.  D.

【解析】 因为＝λ＋μ＝λ(＋)＋μ(＋)＝λ(＋)＋μ(－)＝(λ－μ)＋(λ＋μ)，所以 解得 所以λ＋μ＝.

方法点拨：(1)平面内的任何向量都可由基底唯一表示出来，因此，若有c＝λa＋μb，则可转化为确定待定参数λ，μ的问题，从而可通过建立方程组，利用解方程的方法进行解决．

(2)用平面向量基本定理解决问题的一般思路是先选择一组基底，并运用该基底将条件和结论表示成向量的形式，再通过向量的运算来解决．

考点4：向量的坐标运算

例4.(1)已知平行四边形ABCD的三个顶点A，B，C的坐标分别为(1,0)，(0,2)，(－1，－2)，则顶点D的坐标为__________．

(2)向量a＝(2，－9)，向量b＝(－3，3)，则与a－b同向的单位向量为(   )

A．(，－)  B．(－，) C．(，－)  D．(－，)

 【答案】：(1)(0，－4)； (2)A

【解析】：(1)设D的坐标为(x，y)，

因为四边形ABCD是平行四边形，所以＝，

所以(0,2)－(1,0)＝(－1，－2)－(x，y)，

所以(－1,2)＝(－1－x，－2－y)，

所以所以

所以D的坐标为(0，－4)．

(2)由已知得a－b＝(2，－9)－(－3,3)＝(5，－12)．

所以|a－b|＝＝13，

所以与a－b同向的单位向量为(a－b)＝(，－)．

方法点拨：1)向量相等就是两向量的坐标对应相等．

 (2)注意如下结论的运用：①当向量的起点在原点时，P点的坐标就是向量的坐标；

②若A(x1，y1)，B(x2，y2)，则向量＝(x2－x1，y2－y1)；

考点5：向量的数量积、模

例5.已知|a|＝2，|b|＝3，a与b的夹角为120°，则：

(1)(2a－b)·(a＋3b)＝____________；(2)|a＋b|＝__________.

【答案】：(1)－34；(2)

【解析】：因为|a|＝2，|b|＝3，a与b的夹角为120°，

所以a·b＝|a||b|cos 120°＝2×3×(－)＝－3.

(1)(2a－b)·(a＋3b)＝2a2＋5a·b－3b2＝2|a|2＋5a·b－3|b|2＝8－15－27＝－34.

(2)|a＋b|＝＝＝＝.

方法点拨：(1)求平面向量的数量积的基本方法：①利用定义；②利用坐标运算；③利用运算律；(2)利用：①a2＝a·a＝|a|2或|a|＝；②|a±b|＝＝；③若a＝(x，y)，则|a|＝.

考点6：向量的夹角

例6.【2019年高考全国I卷理数】已知非零向量a，b满足，且b，

则a与b的夹角为

A．      B．     C．     D．

【答案】B

【解析】因为b，所以=0，所以，所以=，所以a与b的夹角为，故选B．

方法点拨：经常用到数量积的定义、模、夹角公式，尤其对|a|＝要引起足够重视，它能实现模与数量积的转化，是求距离的常用方法．

考点7：向量数量积的综合运用

例7.（2019年高考天津卷理数）在四边形中，， ， ， ，点在线段的延长线上，且，则__________.

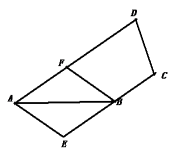【答案】.

【解析】

解法一：如图，过点作的平行线交于，

因为，故四边形为菱形。

因为，，所以，即.

因为，

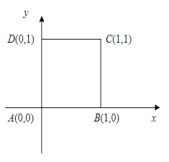
所以.解法二：建立如图所示的直角坐标系，则，。

因为∥，，所以，

因为，所以，

所以直线的斜率为，其方程为，

直线的斜率为，其方程为。

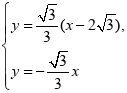由得，，

所以。

所以。

方法点拨：

(1)与几何背景相关的数量积计算问题，其基本思路有：①基向量法；②坐标法．

(2)当几何图形是特殊三角形或四边形时，一般采用坐标法，即通过建立直角坐标系的方法，将其转化为向量的坐标运算．

考点8：向量与三角变换的综合

例8. 已知向量a＝，b＝(cos x，－1)．

(1)当a∥b时，求cos2x－sin 2x的值；

(2)设函数f(x)＝2(a＋b)·b，已知在△ABC中，内角A，B，C的对边分别为a，b，c.若a＝，b＝2，sin B＝，求y＝f(x)＋4cos 的取值范围．

解析：(1)∵a∥b，∴cos x＋sin x＝0，

∴tan x＝－，∴cos2x－sin 2x＝＝＝.

(2)f(x)＝2(a＋b)·b＝sin ＋，

由正弦定理得＝，可得sin A＝.

∵b＞a，∴A＝，y＝f(x)＋4cos＝sin－.

∵x∈，∴2x＋∈，∴－1≤y≤－，

即y的取值范围是.

方法点拨：平面向量与三角函数综合的这类题目的解题思路通常是将向量的数量积与模经坐标运算后转化为三角函数问题，然后利用三角函数基本公式求解.解决这类问题涉及的知识有:①向量的坐标表示，向量的加法和减法；②实数与向量的积，两向量的数量积；③两向量平行、垂直的充要条件；④向量的夹角、长度等.

考点9： 向量与圆锥曲线的综合

例9.已知动点到直线的距离是它到点的距离的倍．

（1）求动点的轨迹的方程；（2）设轨迹上一动点满足：，其中是轨迹上的点，直线与的斜率之积为，若为一动点，，为两定点，求的值．

解析：（1）点到直线的距离是到点的距离的倍，则

，化简得．

（2）设，，，则由得，

，

因为点在椭圆上，所以，，，

故

设，分别为直线，的斜率，

由题意知，，因此，

所以，所以点是椭圆上的点，而，恰为该椭圆的左右焦点，所以由椭圆的定义，．

方法点拨：向量与解析几何都具有数形结合的特性，在它们的知识交汇处的命题通常涉及到夹角、平行、垂直、共线、长度等.解决向量与解析几何相结合的问题，通常是用向量的坐标运算把已知条件中的两向量平行、垂直、共线、长度等问题转化为解析几何中的条件，使问题坐标化、代数化、符号化，从而应用代数运算来处理解析几何中的相关问题.