高等数学中的伽玛函数浅析

高等数学中的伽玛函数浅析

杨德彬

哈尔滨华德学院  数理教研部 黑龙江省 哈尔滨市 150025

摘要  在高等数学（高等数学）的反常积分审敛法一节课中对伽玛函数（函数）进行了简介，但实际上伽玛函数在现代数学各个分支中都有所涉猎，在微积分、概率论、偏微分方程、组合数学，都起着重要的作用。尤其是在研究生入学考试的概率论与数理统计部分，经常用到伽玛函数，但很多考生对伽玛函数了解不是很透彻，原因是在学习的时候，教师很少对伽玛函数进行详细的介绍，本文针对这个问题，将从伽玛函数的起源到性质再到应用，进行逐一介绍。

关键字  伽玛函数  微积分  概率论

一、伽玛函数的起源

说起伽玛函数的起源，不得不提的一位英国数学家约翰·沃利斯（1616-1703），他毕业于剑桥大学伊曼纽尔学院，对现代微积分的发展有着重要的贡献.他在无穷小分析领域里有着独到的建树，在计算的值时，他就已经领先于欧拉论述伽玛函数的某些作品.在1655年沃利斯写下了一个神奇的数学公式，这不仅是数学史上较早的无穷乘积的例子，也是第一个将表示成容易计算的有理数列的极限的公式.后来我们把形如的公式称为沃利斯公式.可见沃利斯公式天然和阶乘有着紧密的联系.现在我们知道这个积分代表了半圆的面积，因此，这个面积是.但是，当时沃利斯给不出这个答案，但他的归纳法和插值法产生了一个十分有趣的结果，在针对的几个正整数值求出的值之后，沃利斯通过不完全归纳法得出了这样一个结论：这个积分的值是.假设这个公式也适用于的分数值，沃利斯得出结论：，式中，或者.这是欧拉的贝塔函数的一个特例，即：式中，.虽然沃利斯并没有显示地提出把阶乘推广到分数的问题，但是他对一些特殊积分式的研究、沃利斯公式的结论以及推导过程却给后来的数学家们进一步研究阶乘提供了许多重要的线索，也为未来伽玛函数的发现埋下了一颗种子.

十七世纪中期，由于帕斯卡、费玛、贝努力等数学家的推动，概率论以及与之有关的组合数学获得了很大的发展，阶乘的数值计算开始频繁的出现在数学家面前，如棣莫弗、斯特林、哥德巴赫都做出来重要贡献。关于伽玛函数的重要人物是欧拉，欧拉在其他数学家的启示下，成功地把表达为了一个非常简介的积分形式，也就是我们常见的伽玛函数的一般形式.

二、伽玛函数的定义与性质

定义  我们称为函数.

根据反常积分审敛法可知，这个积分对均收敛.函数的图像如图所示.

在概率论计算中，我们经常会用到函数，有些性质会方便我们计算.接下来我们不加证明的给出如下常用性质.

性质1 递推公式

性质2 ，其中

性质3 ，另外

    下面看一道应用函数计算的例题，体会一下函数对于积分计算的方便性.

例1  设在上的反常积分收敛，且

，对任意成立，求和.

解 由题设知收敛，因而其值为常数，设此常数为，即，则

，在此式两端在区间上积分，得到

，

故，且.

在计算时可直接利用性质3可得，

.

从上面的例题可以看出，在计算反常积分的时候，如果符合函数的形式可以直接利用其性质结果进行代入，如果接近函数的形式，可以通过适当的变形，凑微分等手段变成函数的形式，再进行计算.

三、伽玛函数的应用

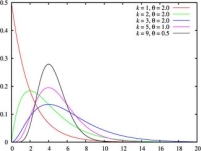
1763年，英国数学家托马斯在《论有关机遇问题的求解》一书中提出了一种运用归纳推理研究统计学问题的理论，经过后来的一些统计学者进行整合和发展，目前已经成为一种系统的统计推断方法，称为贝叶斯统计.伽玛函数在概率统计中也起到了关键的作用。在数理统计中有常见的三大分布（分布，分布，分布），它们的密度公式中都有伽玛函数的身影。但有一种分布是直接由伽玛函数变换得到的伽玛分布.伽玛分布是一种连续概率函数，其中的参数为形状参数，为尺度参数.密度图像如右图所示.

伽玛分布的概率含义为假设随机变量，为等到第件事发生所需之等候时间.我们令，且令，即，概率密度函数为.

伽玛分布在概率统计领域中很重要，众多统计分布和它都有着密切的关系.指数分布和分布都是特殊的伽玛分布.另外伽玛分布是一个很强大的先验分布，在贝叶斯统计分析中被广泛的用作其他分布的先验.

例2 设随机变量独立同分布，同服从参数为和的正态分布，试证明：不是的无偏估计.

证明：由于随机变量独立同分布，则这些变量都服从正态分布，那么便服从自由度为的卡方分布，则.因此

，

则，则不是的无偏估计.

参考文献

[1]刘恒，李冠军. 数学分析教学中欧拉积分的推广与应用.［J］．湖北第二示范学院学报，2019，36（8）90-91

［2］周占杰． 伽玛函数和贝塔函数在概率统计中的应用 ［J］． 电大理工，2009( 1) : 59 － 62．

［3］楼红卫． 伽马函数余元公式的证明［J］． 高等数学研 究，2017，20( 1) : 1 － 4．

［5］田兵． 欧拉积分在求解定积分中的应用［J］． 阴山学 刊，2009，23( 3) : 22 － 24．

［6］卢路加，张君会，赵志稳． 欧拉积分性质及应用［J］． 亚太教育2015( 20) : 222．

作者简介

杨德彬   1982年2月   女   汉   黑龙江省哈尔滨市  硕士研究生   副教授  研究方向：   高等数学