“双减”政策下赏析中考试题的设置

“双减”政策下赏析中考试题的设置

周明和

（安徽省马鞍山市新市初级中学 243141）

摘  要：中考压轴题基于学生的最近发展区来设置问题，让学生在积累的基础上，通过合理猜想，联系相关知识与相近的问题，调动已有的经验，达到解决问题的探索经历，在学生独立自主的探索过程中，落实培养学生的数学核心素养，体现数学学习的价值。在“双减”背景下，通过对压轴题的理解与赏析，达到平时教学中数学的题量要作“减法”同时，要在题的“品质”上做“加法”。

关键词：猜想；一线三等角；半角模型；A字型与8字型

引  言：出题人立足于基础，让学生的思维落地有“根”，这样的试题才是“好”题，让学生回归于数学本源，也能凸显数学的核心素养。这样题目积极响应“双减”政策。为老师的教学指明了方向，不搞“偏、怪、难”的题目。

1.试题呈现

（安徽省2022年中考填空14题）如图1，四边形ABCD是正方形，点E在边AD上，是以E为直角顶点的等腰直角三角形，EF，BF分别交CD于点M，N，过点F作AD的垂线交AD的延长线于点G，连接DF，请完成下列问题：

（1）＝ °；

（2）若DE＝1，DF=，则MN＝。

2. 试题评价

2.1简洁语言，内涵丰富

本题以正方形与等腰直角三角形为背景设置问题，图形简洁，言语简练，层次分明，将全等三角形、平行线分线段成比例、一线三等角、A字模型与8字模型等内容很好地融合在一起，这两问自然连贯，相互关联，拾及而上，体现了“平和中见关爱，自然中显素养”的命题特征。

第（1）问，由题目条件易推导出，理由是AAS，再全等三角形的性质可知AB=EG=AD，AE=GF，自然得到DG=GF，所以为等腰直角三角形，从而得出，此问起点不高，大多数同学能轻松解答。

第（2）问在限定条件下，求线段MN的长度，难度比第（1）问有所提升，要求学生要拓展思维、运用逻辑推理与几何直观的能力。我们解题的视角由平行线、相似三角形、一线三等角、半角模型、A字型与8字型等，展开联想也能找到解决问题的方法。

2.2注重思维开放，渗透数学思想

本题作为填空题的压轴题，也承载着选拔与区分的功能。它综合考查“图形与几何”板块的核心内容（全等三角形、相似三角形的判定、平行线分线段成比例等）。突出考查学生的逻辑推理能力、几何直观、比例式运算能力等。渗透了数学的转化思想。第（1）问虽然简单，但也需要学生有一定的几何直观与逻辑推理能力为基础的，对于一线三等角模型熟练的同学很快解决问题，如图2所示。第（2）问，知识点多，切入点也多，要抓不住关键点或思维打不开，就不易解决。此问能充分暴露学生思维的灵活性，还有知识点的迁移与关联性，数学模型的应用性。

2.3回归数学的本源，培养数学的核心素养

这样的压轴试题立足于数学的本源，文字语言简洁，让学生入手容易，感觉能做，但想轻松解决是不易的，涉及到的知识点细想很多的，如直角三角形两角互余；等腰直角三角形有特殊角45°；有一组平行线；提供的着眼点很多，我们思路也得到相应的拓展，涉及到核心素养有数学抽象、逻辑推理、直观想象等。

解法方法也是多样化的，等腰直角三角形联想一线三等角的基本模型；平行线联想到平行线分线段成比例；45°与直角联想到半角模型；平行线联想到A字型与8字型。呈现思维解法的发散性，解法的个性化，彰显数学思想与数学方法。

3. 解法赏析

视角1：构造平行线，利用A字型与8字型相似。

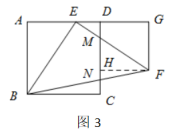
解法1-1：如图3由DE=1，DF=，易得DG=GF=2。过F点作，垂足为H，易知四边形DGFH为正方形，DH=GF=2，又由于，得到，得到，易得线段，，因此。

解法1-2：如图4所示，添加辅助线，通过两个A字型相似，也可解决问题。留给同学们自己独立完成

视角2：平行线分线段成比例与A字型与8字型相似。

解法2: 延长线段FE交BA的延长于点K，因，得，所以得，从而得到；

视角3：45°与直角构成半角模型。

先回顾一下半角模型，如图6所示，ABCD是正方形，且，则有。（同学们自己去证明一下）

解法3: 过F点FW垂直于CD，易知GFWD是正方形，截取VG=NW，又因GF=FW，，所以，则FV=FN，从而得到，MF=MF，则，设MN=MV=，MD=，则WN=VG=，在中，有，得。

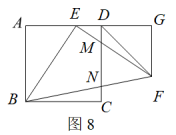
视角4：相似三角形对应边成比例。

解法4: 如图8所示，在和中，有，，得到，从而有，又因，所以,，又因在中，有，从而得到，则有，,，得。

4. 反思

命题人预估学生的状况，也为了落实“减负”，从而降低题目的难度，一个填空题的5分，于是分割为一个简单的填空题2分，一个较为有思考力的3分。通过以上分析，我们得出这样一个结论，平时教学中，要适时“减轻”学生的负担，自己要精心选择典型的例题，题目要具备思维的灵活性、思路要多样性，让学生有想法，贴近学生的发展区内，但也不易轻松解决，具备思维的深刻性，平时的试题与教学都要注重回归数学的本源，要凸显数学的核心素养。

参考文献

[1]柳 军，王志刚.回归本源 凸显能力[J].中学数学教学参考（中旬），2021（8）：43-45.

[2]余旭红.指向数学学习能力提升的“四学”课堂例析[J].中学数学教学参考（中旬），2021（5）：13-16.