电磁振动发电机磁场特性与谐振频率分析

电磁振动发电机磁场特性与谐振频率分析

肖丽  ,张慧芳

天津商业大学，天津 300134

摘要：本文采用有限元分析法对永磁式振动发电机的谐振频率进行研究与分析。基于Ansys/Maxwell软件计算该类电机磁轭等部分的电磁力，并计算电机磁轭中不同位置处的磁感应强度及其变化规律，从而获取其轭部沿运动方向所受电磁力的分布特性与谐振频率特性。

关键词：磁场特性；谐振频率；有限元分析法；振动发电机

1 引言

永磁直线振动发电机是基于永磁电机与直线发电机的结构与工作原理设计而成的。该类电机具有发电功能，不仅可实现便携式发电，还可用于海洋发电。此外，这类电机还可嵌入汽车减震装置，以完成减震器内的振动能量转化为电能。

由于永磁振动发电机广泛应用于能量转换装置，所以本文采用有限元分析法建立该类发电机模型，并基于Ansys/Maxwell仿真软件计算与分析其静态特性与谐振频率特性，所得结果可对该类电机优化设计与控制方法的研究具有一定理论指导意义。

2 电磁振动发电机基本结构

磁轭与振子是电磁式振动发电机的重要部分。本文所研究的发电机磁轭部分为E型结构，并在两侧缠以绕组。该类电机磁轭高度与磁轭间距直接影响发电机磁场的最大效率，而磁轭前端面高度与磁轭宽度直接受到磁感应强度最大值在饱和状态所能承受的条件所影响。E型磁轭发电机的每个线圈以串联方式独立连接，以提高电机输出电压。为使电机获取更多的能量，电机可适当地增加磁极对数或是提高磁轭的纵向高度，但增加的磁极对数与磁轭的纵向高度均应在允许条件内。

对于振子结构，该类电机采用圆柱形奥氏不锈钢型的振子，振动轴中间部位凹陷，两端部位凸出，其中间部分异相排列三块永磁体，永磁体采用圆形状，每块永磁体间的圆心距尺寸为30毫米，其外径为25毫米。振动轴的两个末端设置方槽用于安装平键以避免振子在高速振动中产生偏移现象。此外，振动轴还采用圆法兰对其进行位置限制，这样可以抑制发电机振动过程中吸力所引起的额外转动。

3 电磁式振动发电机谐振频率分析

振动发电机矢量磁位方程如式（1）

       （1）

其中，V代表运动物体的实时速度，A表示磁矢量， J则为电流密度。

与空气隙中存储的磁场能量相比，存储于磁轭部分的磁场能量甚为微小。由于磁轭内部磁场强度很小，故存储在磁轭部分的磁场能量远小于存储在空气隙中的部分，故前者忽略不计，气隙磁场总能量为

     （2）

式中，，V、B、H分别表示为场域的体积、磁感应强度与磁场强度；L与S分别表示气隙长度与磁轭表面积；μ0代表真空中磁导率。

根据虚功法原理[1]，电磁力通过计算整个单元能量对单元节点坐标的微分而得

（3）

其中，Fxi为节点i电磁力的x分量（y或z分量），xi为节点坐标（x、y或z坐标），V为单元体积。利用该法计算电磁力时需对该单元的任何一个节点加以计算，再将计算出所有节点上的力施以求和运算。同时，根据单元形状法[2]，通过可移动部件的位移微分获取电磁力，通过对物体四周空气层的所有力施以求和则可获取所求物体的总力，如式（4）所示。

（4）

其中，Fs表示S方向上的单元力，代表磁场强度对位移的微分，V为单元体积，S表示节点坐标分别在X、Y、Z方向上的虚位移。在发电机振动过程中，其电磁力如式（5）所示

（5）

鉴于振动发电机具有对称型的基本结构，在x方向与y方向上的虚功电磁力则可以相互抵消，因而该发电机所受的电磁合力方向沿z方向，如式（6）所示。

（6）

将永磁振动发电机磁轭作为一个整体来研究其受力情况，计算振子沿z轴方向不同位置时，磁轭中磁感应强度x轴分量Bx变化曲线，如图1所示。对z方向位移求偏导数得到Bx 沿z轴变化率曲线，如图2所示；磁轭中磁感应强度z轴分量Bz变化曲线，如图3所示。对z方向位移求偏导数得到Bz沿z轴变化率曲线，如图4所示。由于磁路的特殊结构，磁感应强度y轴分量By几乎为0，而且运动过程中量值基本不发生变化，因此磁轭中磁感应强度y轴分量By 沿z轴变化率可以忽略不计。

图1　磁感应强度x轴分量           图2　Bx 沿z轴变化率

图3　磁感应强度z轴分量       图4　Bz沿z轴变化率

当振幅数值的选取范围为{-5 mm，5 mm}，振动发电机的振子所受电磁力与轨迹位移呈现线性分布状态，由便可知弹簧的刚度取值为10N/mm，其固有频率，此处m代表振子的质量。因而，可得到ωn=11.25 Hz。当外界的振动频率与弹簧ωn数值相等时，系统才能够输出较为理想的能量状态。

在此基础上，本文还采用等效电路法对该类电机的谐振频率进行计算分析。首先进行电机线圈匝数确定，文献[4]分别对匝数为100~700时电机磁感应强度与输出电动势进行研究，结果表明当匝数为500时电机输出感应电动势曲线、磁感应强度曲线斜率上升趋缓，呈现饱和趋势。故匝数确定为500。电机阻抗匹配等效电路如图5所示，R1为传输线路电阻和负载电阻，L为电感负载。

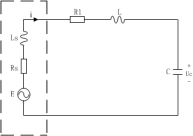
图5 等效电路图                         

    电机线圈匝数数目的增多，线圈中感应电流也随之增大，磁感应强度B随之减小，感应电流下降，故单一方面增加匝数，感应电动势可达上限，线圈内部磁感应强度随匝数变化如图6所示。

图6 磁感应强度随线圈匝数变化

    当匝数一定时，相对磁导率越高，输出电压越大，当相对磁导率一定时，在某个阶段增大线圈匝数，输出电压也会随之增大，但是当匝数增大到一定程度时，曲线斜率比较平滑，说明此时如果再增大线圈匝数，输出电压将趋于不变，因此，绕组匝数要根据实际需要确定。

4 总结

本文主要研究电磁式振动发电机的结构进行分析，分别采用虚位移法和等效电路法对该类电机的谐振频率进行计算，并对频率特性进行分析。

参考文献：

[1] 王志华,张少鹏,姚涛,吕殿利,张惠娟.振动发电机的系统建模与频率特性分析[J].电工电能新技术,2017,36(11):57-62.

[2] 罗翠线,秦敏哲.基于模态分离技术的3×n阵列式低频宽带压电振动发电机的设计研究[J].电子学报,2020,48(03):554-560.

[3] 李恒,王博文,李娜,邹尊强.电磁式振动发电机的机电特性分析与实验研究[J].微电机,2016,49(03):10-13+30.

[4] 张露予,李志鹏,王博文,王志华,李雨婷.电磁式振动发电机结构设计及谐振频率分析[J].河北工业大学学报,2014,43(01): 1-3+14.

项目资助：天津市高等学校科技发展基金项目（项目编号：2018KJ227）