高考数学新题型的应对策略研究-中国期刊网

首页 > 《教学与研究》 > 2022年14期 > 高考数学新题型的应对策略研究

（整期优先）网络出版时间：2022-11-02

作者: 黎冠芬

文化科学 >教育学

打印

同系列资源

/ 2

高考数学新题型的应对策略研究

黎冠芬

广东省四会市四会中学，广东肇庆，526200

【摘要】：在高考数学不断改革的背景下，考试形式以及考试内容的改革迫在眉睫。在普通高中数学课程标准中对于数学考试提出了更为明确的要求，如对高考题型和结构进行改革等。在这样的指导思想下，近些年来的高考数学新题型不断推陈出新，如综合性问题、多项选择题，双空填空题、选择论述题型、策略开放题型、数学作文题型等。在本文的研究中，结合这些新题型的特点展开深入地分析，并提出了相应的应对策略。

【关键词】：高考数学；题型；新题型；应对策略

1、前言

高考一直以来都是我国选拔人才的基本教育制度，对于国家人才发展战略的实现起到了至关重要的作用。从我国开始实行高考制度，经过几十年的发展，我国的高考制度不断完善，为国家选拔出了大量的人才。从目前的发展情况来看，我国已经步入了高等教育普及化阶段，国家不断地深化与改革高考招生制度，在考试制度中，明确地提出要设置好题量、提高试卷的信度与效度、试卷不断地提高开放性等要求，要更加地注重学生创新能力和逻辑思维能力的培养。从整体上来说，当前的高考数学灵活性增强，各类新题型也逐渐地出现在试卷中，在以后的题型设计中，新题型的设计将会更多、更普遍。因此，结合目前的考试内容，对高考数学新题型的应对策略进行分析对于学生学习思路的转变有着非常积极的意义。

2、研究高考新题型的目的

2.1、改善高中数学现有题型的不足

从目前高考数学的题型来看，各类题型的数量以及分值基本上确定，但是从目前的考试指导思想来看，要求着重培养学生的创新能力和逻辑思维能力，全面地提升学生的核心素养。从这些年的题目来看，灵活性加大，考察的方式也更加多变，因此，对新题型进行研究有助于调整日常数学教学的思路，补充现有的题型，对于学生核心素养的提升非常有帮助意义。

2.2、促进学生创新能力的培养

党的十九大报告明确地提出要加快建设创新型国家，从数学领域来看，数学创新能力是一种特殊的创新能力，具体可以理解为提出数学问题的能力和质疑的能力，会使用新的数学模型并且运用于实践的能力。而在研究当前高考中出现的新题型对于学生的创新能力有着一定的导向作用，在研究与破解新题型的过程中培养学生的数学创新能力。

3、高考数学新题型的应对策略分析

3.1、综合性问题研究

综合性问题在目前高考数学的考察中非常普遍，可以出现在各类题型中，遇见这类问题，学生们需要先从基础知识出发，分析题目中的问题，将复杂的问题化解为单个的问题一个个击破即可，这类综合性问题在最值问题中考察最为常见。首先，最值问题与几何问题结合起来考察也是当前高考命题的一个方向，对于几何中的最值问题类型比较固定，也相对比较简单，下面简单介绍几种解题方法。

方法一：代数法。该方法就是将所求的模型变成某个变量的函数，再使用函数最值的求解方法进行求解即可。

例1 已知直角梯形ABCD中，AD∥BC，∠ADC=90°，AD=2，BC=1，P是腰DC上的动点，求|PA+3PB|的最小值。

解：根据题意，我们采用数形结合的方法来解答这一道题。以D为原点，以DA，DC所在的直线为x轴，y轴，建立平面直角坐标系，设DC=a，DP=x，x[0,a]，则D(0,0),B(1,a),C(0,a),P(0,x),因此可以得出，PA=（2，-x），PB=(1,a-x),也就是说，PA+3PB=（5,3a-4x），所以|PA+3PB|2=25+（3a-4x)2≥25,因此，可以得出|PA+3PB|的最小值为5。

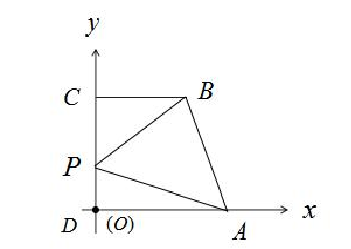
IP}S64243[FO4@_WE@~11IV

图一：例1图形

方法二：导数法。导数法在求最值的过程中应用非常广泛，该方法也是高考数学中常见的考察类型。

例2 圆形纸片的圆心为O，半径为5厘米，该纸片上的等边三角形ABC的中心为O。D、E、F分别是圆O上的点，∆DBC、∆ECA、ΔFAB均是等腰三角形，沿着虚线剪开之后，分别以BC、AC和AB为折痕折叠∆DBC、∆ECA和ΔFAB，从而使得D、E、F相互重合，得到一个三棱锥，那么问：当∆ABC的边长在不断地变化过程中，所得到的三棱锥体积的最大值为多少？

这道题看起来非常复杂，我们可以先对题目进行整体上的把握，然后将OD连接起来，那么BC与OD相交与点G，由题意可知，BC与OG是相互垂直的，由此可以得出，也就是说OG与BC之间是呈现出正比例的关系，我们假设OG=x,那么 BC=2x，DG=5-x，

那么我们就可以计算出三棱锥的高，也就是,

即h=，那么我们接着就可以求出三角形ABC的面积，

即S=2x×3x×=3x2 则体积V=Sh=x2×，接着我们再用换元法，令,x(0,),那么我们对函数f(x)求导，得出

,令，得出f(x)≤f(2)=80,

也就是说V≤×=4。

所以，所得到的三棱锥体积的最大值为4cm3

最后，对于实际应用问题中的最值题目，题目的资源非常丰富，但是基本上与学生们的日常生活结合紧密，函数实际应用过程中的最值问题不仅仅是教学工作的重点，也是教学中的难点，学生们在解答这一类的应用题目时，必须具有较强的综合能力，找到题目已知条件中变量中不变的最值点，建立正确的数学模型，从而对题目进行解答。

例3 某公司计划使用2160万元购置一块空地，打算在该空地上方建造一栋超过10层的楼房，且面积均为2000平方米，通过对经费的测算，如果楼层大于等于10层，那么每一平方需要耗费560+48x的费用，那么问题是如果想要每平方米的费用最低，那么应当建造多少层合适？（平均购地费用=购地总费用/建筑总面积，平均综合费用=平均购地费用+平均建造费用）。

当拿到这个题目的时候，感觉条件有点杂乱无章，那么我们首先需要对题目给出的条件进行梳理，然后建立目标函数，最终求出最值。

解：设每一平方米的平均综合费用为f(x)，那么

f(x)=（560+48x）+

=560+48x+，（x≥10）

那么我们就可以利用基本不等式法来求出函数的最小值，也就是说当48x=的时候，等号成立，解得x=15，因此可以得出当楼房为15层的时候，每平方米的费用最低。

3.2、选择论述题

在目前的高考题中，选择题是必不可少的，该题型对基础知识以及综合知识的考察有着很好的作用，而且从特点上来看，选择论述题只要求在四个选项中选出正确答案，从目前的考察情况来看，选择题的四个答案往往具有很强的相似性，近些年出题的灵活性也非常强，针对这类题目学生先读懂题目内容，分析出考察的知识点，不管题目描述的多么复杂，学生只需要抓住核心内容精准地分析问题即可。

例4 一台显示器上面有40个数字，人们可以通过遥控器对显示器的数字进行增加与减少，遥控器上有两个按钮，若从增加和减少两个按钮中选择一种按下，按照这种方法一共按六次，显示器上仍然显示40个数字的概率是（）

A. B. C. D.

解题思路：该问题在高中数学中属于排列和组合的问题，虽然题目的描述比较复杂，但是学生需要抓住关键词语进行分析，从题目中看出按六次数字不变,说明有三次增加和三次减少，那么从这个角度来说，增加和减少的概率为p= ，所以结果就应当为p3（1-p）3= ，所以这道题目选择选项B。

3.3、新定义题

新定义问题总的来说题型较为新颖，可以一个新的概念、新的符号或新的运算法则,也可以是新知识背景试题等。由于新型题对学生来说是相对陌生，考试的时候时间紧，学生压力也大，对学生的心理素质和随机应变能力要求比较高。对这种新定义问题，学生要认真阅读，理解规则，把新定义问题转化为旧知识，理解其本质就能解决问题。

例5 已知函数f(x)及其导数f'(x),若存在x0使得f(x0)=f'(x0),则称x0是f(x)的一个“巧值点”,给出下列四个函数:①f(x)=x2;②f(x)=e-x;③f(x)=ln x;④f(x)=tan x,其中有“巧值点”的函数是(　　)

A.①② B.①③ C.①③④ D.②④

解题思路：新定义“巧值点”的本质就是方程f (x)=f '(x)有没有解的问题，所以可以转化为函数零点的求法。①f(x)=x，f '(x)=2x，由x2=2x, 直接解得x=0和x=2，所以有“巧值点”；②f(x)= e-x,f '(x)= -e-x,由-e-x= e-x，此方程无解，所以无“巧值点”；③f(x)= ln x,f '(x)= ，ln x= ，令g(x)=ln x- ，g(1)= -1<0,g(e)=1->0。由函数零点存在定理，得g(x)在区间(1,e)上必有零点,即f(x)有“巧值点”；④f(x)=tan x，f '(x)= =tan x，得sin xcos x=1，即sin 2x=2，此方程无解，所以f(x)无“巧值点”。所以有“巧值点”的是①③，故选B。