层次分析法在水电机组优化组合应用中的改进方法

层次分析法在水电机组优化组合应用中的改进方法

韦,东

钛能科技股份有限公司  210000

1 引言

    截止到2021年底，我国水电装机容量达到3.9亿千瓦，约占全国发电总装机容量的16.4%左右。伴随我国生产力水平和人民生活水平的提高，社会用电量逐年攀升。加之在“双碳”目标下能源结构优化需求，尽管面临越来越大的环保压力，未来我国水电发展空间依然广阔。

同大多数技术的发展过程一样，运筹学最初也是用来解决军事问题的。但应用于水电站的优化运行，至今也有七十多年的历史了。初期采用等微增率法、线性规划，再到动态规划等全局最优解法。全局最优解法主要基于机组设计时的特性函数，而非实际运行时的特性数据。但众所周知，水电厂中实际安装的机组即使型号、容量完全一致，他们的动力特性也多少有些差异的。所以后来学者们又提出了基于神经网络、遗传算法、鱼群算法等局部最优解法。目的是在不同容量、不同型号的机组间，在顾及安全经济性多目标的前提下，通过优化计算，得到一个可行的较优解。

水电厂的优化运行一般分为机组组合和负荷分配两部分。文献[1]提出了将层次分析法（AHP）用于机组组合的优化。即基于给定的水电厂负荷，在若干个可行的机组组合方案中，选取最优者，使水电厂运行的总效率最高。本文针对文献[1]中提出的机组排序算法提出改进方法。

2 将层次分析法用于机组组合

层次分析法是美国运筹学家匹茨堡大学教授萨蒂于20世纪70年代提出的，最初是用于解决经济问题的多目标决策系统方法。其主要特点是将定性指标通过模糊量化方法进行定量分析，从而对多目标决策方案进行排序比较，得出较优解。

水电厂机组组合需要完成机组的优先级排序，在排序过程中需要考虑的因素较多，如机组效率、机组当前状态、机组运行时间等因素。

首先需建立机组组合的层次结构模型，如图1。

根据准则层的各个要素构建判断矩阵，如图2。

图2中为某一层的判断准则，如“机组总排序”。为受支配的元素，如“机组效率”“停机时间”等。表示对而言，对的相对重要性，一般用1到9或其倒数表示。当其数值越接近1，表示两个元素的重要性越接近。 不难看出，矩阵中元素具有：

        （1）

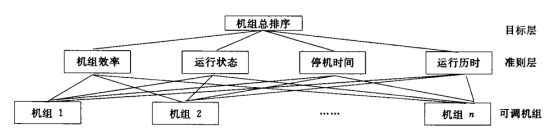
图1 用于机组排序的层次结构模型

图2 水电机组优化判断矩阵

当判断矩阵具有：

（i，j，k = 1，2，3，⋯，n）（2）

则称判断具有一致性。如何保持判断矩阵的一致性，在层次分析法的应用中是重点也是一个难点。

对应于判断矩阵最大特征根的特征向量，经归一化（使向量中各元素之和等于1）后记为ω。ω的元素{}即为同一层次因素对于上一层次因素相对重要性的排序权值。用{}分别乘以各元素的值，即可得到开机优先顺序。再根据负荷曲线和备用容量要求，即课确定组合方案。

3 层次分析法在水电机组组合应用中的改进

正如前面所述，如何保持判断矩阵的一致性，在层次分析法的应用中是重点也是一个难点。理想情况下，当且仅当=n时，具有完全一致性。当应用于水电机组排序时，受矩阵规模的影响，往往矩阵规模越大，越难以保持式（2）的一致性。文献[2]提出了一致性指标CI：

（3）

   因CI受n的影响很大，引入与n相关的随机一致性指标RI，如表1：

表1 平均随机一致性指标RI标准值

再将CI和RI进行比较，得出检验系数CR如下：

（4）

一般情况下，认为CR不大于0.1时，判断矩阵具有较满意的一致性。这个“满意”的一致性，就是层次分析法在水电机组排序中的难点。在文献[1]中，共考虑了“机组效率”“机组运行状态”“机组运行时间”和“机组停机时间”四个元素。判断矩阵的形成是采用专家打分法，即请行业专家根据经验对每个进行赋值。形成矩阵后，计算CR，如不大于0.1，即认为矩阵的一致性是“满意”的。如果“不满意”，需对矩阵进行调整，直到“满意”。

在这一过程中，值得商榷和改进的主要有几点。一是只考虑四个元素是否太“少”？如机组寿命、大修周期、机组可靠性等是否也可以放到矩阵中。二是对于那些排序靠后的机组如何改进？实际上对排序靠前的机组同样需要进一步改进。三是所考虑的四个元素具有不同的量纲，每个元素取不同的量纲，对最后得出的优先顺序有很大的影响。如对于时间元素，量纲取日、小时、分钟时，在数值上对排序结果的影响是相差很大的，专家在打分时，必须要考虑这个因素。而这个“考虑”是很难量化的，实际情况是判断矩阵的一致性和人类思维的一致性往往难以达到一致性。

如前所述，增加元素数量，意味着判断矩阵的阶数将增大，专家打分时较难保证判断矩阵的一致性。为提高专家打分的一致性，文献[3]提出了一种“三角形调查表”，即先将各元素按重要性大小排序，然后“引导”专家通过、的值确定的值。如、，则推算出 。这个方法可以一定程度上提高矩阵的一致性，方法的难点在事先排序上，因为层次分析法通常要解决的就是多层次的排序问题，而不仅仅是人为排序后再确定权重。笔者提出一种提高矩阵一致性的方法，即设计一个小程序，在专家打分过程中，根据已给出值的矩阵项，按照一致性要求，推算出其他暂未给出值的矩阵项，作为推荐值给专家参考。这种方法可以大幅提高较大阶数矩阵的评价效率。

文献[4]提出了采用模糊数学的方法，对排序的元素建立Fuzzy模型进行计算，从而找出各元素的薄弱环节进行改进。此方法也可用于水电站的设备运行和维护，通过量化分析，逐渐完善更适合本电站特点的设备运维方案，从而创造更大的效益。只是文献[4]的方法是用于离线的分析，在用于水电站的实时控制时，可将专家根据不同数据区间确定的评价集存表，在实际排序时调用。例如在文献[1]中表4的基础上，增加专家对机组1的各元素的状态判断后，得出表2：

表2 机组1状态评价集

注：① 停机状态=停机时间/最大停机时间；

② 运行率=1-大修后运行时间/大修后总时间。

对机组1进行综合模糊评价：

         （5）

从评价结果看，机组1总体上处于“一般”或“较差”的状态。再分析评价集矩阵会发现，主要在“停机状态”方面，专家的评价较低。

目前大多数水电站都配备有计算机监控系统，可利用系统采集的历史运行数据和设备参数，采用自学习的算法对各排序权重进行修订。同时随着数据越来越丰富，也可增加元素数量，即使评价指标更加细化，从而使得排序权重也能随着数据的积累更适合本电站的实际情况。

参考文献：

[1]韦 东 熊曼丽 李光熹. 调峰水电厂的动态机组组合方法. 电网技术,Vol.21 No.2 1997

[2]许树柏. 层次分析法原理. 天津大学出版社 1988

[3]张琦 西村昂. 提高层次分析法评价精度的几种方法. 系统工程理论与实践，1997，11

[4]王振. 基于FAHP-模糊层次分析法的港口综合竞争力评价. 水运工程，2011，2