向量在立体几何中的应用

向量在立体几何中的应用

何彦华

山东省诸城第一中学262200

摘 要：随着新一轮新课改的不断推进，空间向量已被广泛地运用于立体几何中，并显示出其强大的施工优势，因此，有关教育工作者应加强对空间向量的研究。本文通过实例探讨了立体几何中的空间向量。

关键词：高中数学；空间向量；立体几何；应用

引言：

在高考的时候，立体几何这类题，已经成为了重点，虽然大多数问题都属于中等偏上的，但老师们也要注意。在求解空间、平面等复杂问题时，向量可以减少考题难度，并能有效地解决问题。新课程标准引入了新的教学内容，让学生们可以更好的解决立体问题，并进一步说明了空间向量在立体几何中的重要作用。是我们所要学习的一种求题方法。

一、 利用空间向量优化几何题目

高中生的几何问题很简单，就是可以将立体的部分转换为数值，这样就可以让学生更好的掌握。向量的概念在高中数学教学中占有举足轻重的位置，运用向量来求解立体几何问题所带来的优势是普通的数学知识所不能比拟的。我们经常会碰到一些困难的问题，比如用空间的想象力来求解，比如从平面上来判断边界的长短，比如角度等等，但我们可以用向量的概念来进行一些简化的变形，这样就可以很容易地得到它们的边长和角度。运用向量解决问题，不但减少了问题的复杂性，而且给了他们一种新的思考模式，激发了他们创新的思路，激发了他们对立体几何知识的兴趣。

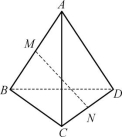
例如：如图所示，已知空间四边形的各边和对角线的长都等于a，点M,N，别是AB,CD的中点，1. 求证:MN垂直于AB,MN垂直于CD,求MN的长。2. 求异面直线AN与CM夹角的余弦值。在这个问题上，我们采用了常规的几何学的方式，首先，我们可以用一个很容易的定理，来验证两条线是垂直的。在求解 MN的长度的问题上，我们需要先做两条辅助线，然后通过几何关系来求长度，而且在求取的过程中会有很多的运算。而通过向量则可以避免这种繁琐的运算。最终我们可以得到一个关于余弦的数值为。

二、 利用空间向量优化解题策略

学习向量的主要目的在于训练学生利用向量的代数方式来解决立体问题，使其能够将复杂的数学问题转换为向量的代数，既方便操作，又提高了数学推理的水平。然而，在解题过程中，我们也需要一些技巧，我们需要对这些问题进行正确的解析，以便在点线面等问题上，以最简便的方法来表达这些问题。其次，采用相应的数学表达式，把该方程代为求解该问题。然后再做一些比较简单的计算，把这个复杂的几何问题给求解出来。

求解一个几何问题，无非就是要得到一个直角和一个夹角，例如： MN垂直于 AB, MN垂直于 CD，求异面直线AN与CM夹角的余弦值。我们使用向量，在空间中设置了一个空间坐标值，然后用垂直关系来验证，由于两条边是垂直的，所以两条边的坐标乘积都是0，再用数值运算就能得到，这要比用常规的方法要简单得多。我们在此基础上，对每个点，每条向量，都建立了它们的坐标，并用坐标法求出余弦和长度，这样又省时，又省力，而且准确率极高。

三、 利用空间向量优化实际运用

在高中的时候，我们可以把向量用于求解一个复杂的几何问题，比如一条直线和另一条直线之间的夹角，一条直线和一个平面之间的夹角，以及一个平面与另一个平面之间的夹角。此外，每个角都有相应的公式，我们可以把它们的坐标代进去。例如，一条直线与一条直线的角度，可以用一条边长来求，一条直线与一个平面的角度，也可以用一条边长来求，而一个平面与一个平面的角度，就可以用向量得到一个三角函数值。

在解决空间角度问题时，我们也可以利用向量解决两条不同平面的直线间的间距和平面间距。求两条异面直线的距离，用一个方程代替不同点的坐标，并用方程求出。与此同时，从一个点到一个平面之间的间距也可以做到。利用空间向量处理立体几何问题，既可以求解线面成角问题，也可以处理面与面之间的距离问题，也可以处理不同面线之间的距离、平行线、面面垂直问题等问题，这些问题都有一个共同的特征，那就是试题都有一定的困难，而且经常会在高中数学试题中出现，但是用常规的解题方式来求解，会很麻烦，因为有了空间向量，就可以把一个简单的组合问题变成一个简单的代数问题。

结束语

随着社会的发展和时代的发展，对高中的数学教育进行改革已成为当务之急。如何有效地提升教学效果，既是对学生的一种考验，也是对老师的一种考验。要实现这一目的，就需要在课堂上不断地改进课堂教学，构建起以学生为主、和谐、平等的教师和学生的关系。然而，尽管课堂的效率在逐步提升，但仍然要求在实践中不断地进行改革与探讨，以提升自己的教学质量，更新教育观念，优化教学方式，运用“空间向量”解决问题，就是一种行之有效的解题方式。

参考文献

[1]张亚斌.高中数学立体几何教学策略分析[J].学周刊,2020(4):19.

[2]郑有礼.浅谈立体几何中空间角的向量原理[J].数学学习与研究,2019(22):109.

[3]黄真同.运用向量法解决高考题中的几何问题[J].数学学习与研究,2018(9):110-112.